Файл: Отчет по лабораторной работе 1 Дисциплина "Физические основы микро и наноэлектроники" по теме Каскадная плавка.docx
Добавлен: 15.03.2024
Просмотров: 17
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНОБРНАУКИ РОССИИ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)
Кафедра МИТ
ОТЧЕТ
по лабораторной работе №1
Дисциплина “Физические основы микро- и наноэлектроники”
по теме:
«Каскадная плавка»
Лабораторную работу выполнили студенты группы 1111
Эсаулова А.
Шмелева Ю.
Удинцев Е.
Преподаватель: Веревкин А.П.
Санкт-Петербург
2022
Цель работы:
Цель работы заключается в исследовании математической модели
фазовых переходов и массопереноса на примере процесса зонной плавки ,
используемой дли очистки веществ от примесей.
Краткие теоретические сведения:
Общее понятие «зонная плавка» охватывает совокупность методов, позволяющих перераспределять растворимые добавки или примеси в кристаллических веществах. Для всех этих методов характерно медленное перемещение узкой расплавленной зоны через сравнительно длинный твердый образец, в результате чего достигается перераспределение примесей.
Подобно тому, как потенциальная энергия в механике U(x,y,z) характеризует положение точки в пространстве координат x,y,z и является функцией положения (состояния) точки в пространстве. В термодинамике также вводятся функции состояния системы в соответствующем “пространстве координат” – термодинамических параметров, например T и V, V и P, P и S, и т. п. К ним относятся:
а) Внутренняя энергия – U (V, T) dU = – pdS + TdS, (1)
б) Свободная энергия – F(V, T) F = U – TS. Ее приращение равно dF = dU – TdS-SdT = – pdV – SdT, (2)
в) Энтальпия – H(S, P) H = U + pV. Ее приращение равно pdV + Vdp = TdS + Vdp, (3)
г) Термодинамический потенциал Гиббса – Ф = H – TS. Его полный дифференциал равен – TdS – SdT = Vdp – SdT (4)
Полезно в число параметров, от которых зависит термодинамический потенциал Гиббса
, включить число N систем.
д) Химический потенциал для систем с переменным числом частиц вводится понятие химического потенциала: M = (dФ/ dN)p,T (5)
В двухфазной системе термодинамический потенциал зависит, кроме P и T, от числа частиц в каждой фазе N1 и N2:
Ф = Ф (p,T,N1,N2).
Следовательно, dФ = – SdT + Vdp + M1dN1 +M2dN2, (6)
где M1 = (dФ/dN1)T,p,N2; M2 = (dФ/ dN2) T, p, N1 . М1 и М2 - химические потенциалы первой и второй фаз соответственно.
Если в системе происходит процесс выравнивания, термодинамический потенциал уменьшается:
dФ < 0. Но: N1 + N2 = N=const и, следовательно, при P, T=const, (M1– M2) dN1 < 0, откуда следует, что dN1 < 0 при M1 >M2 и, ноборот, dN1 > 0 при M1 < M2 т. е. поток вещества направлен от фазы с большим химическим потенциалом к фазе с меньшим химическим потенциалом.
Процессы, с помощью которых происходит установление состояния равновесия называются кинетическими. Если концентрация какого-либо раствора различна в разных его местах, то благодаря тепловому движению частиц (молекул, атомов). Он с течением времени перемешивается: растворенное вещество переходит из мест с большей, в места с меньшей концентрацией до тех пор, пока состав раствора не станет одинаковым по всему объему, этот процесс называется диффузией.
При очистке материалов от примесей методом попроходной плавки стержень этого материала пропускают чрез катушку индукционного нагревателя (рисунок 1). При этом часть стержня, находящаяся вблизи катушки, плавится и перекристаллизируется. А примеси собираются на одном из его концов (смотря по тому, больше или меньше единицы коэффициент сегрегации К.) Расплавленная часть сохраняет свою форму благодаря силам поверхностного натяжения. Процесс плавления (рисунок 3).
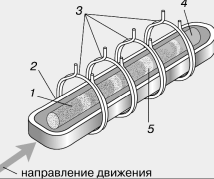
Рисунок 3 – Процесс плавления стержня
При медленном движении загрязненного алюминия в графитовой лодочке относительно индукционных нагревателей вдоль слитка перемещаются расплавленные зоны, переносящие накапливающиеся в них примеси к его концу. 1 - примеси; 2 - графитовая лодочка; 3 - индукционные нагреватели; 4 - чистый алюминий; 5 - расплавленная зона.
Выполнение работы
Варьируя такими параметрами как (Vн скорость нагревателя , l длина нагревателя, положение ВКЛ., ВЫКЛ нагревателя) проведем исследование максимальной очистки металла:
Исследовать зависимость числа проходов зоны, необходимого для очистки β % исходного вещества на α % в зависимости от скорости прохода зоны Vн, отношения L/ l.
Подобрать скорость движения расплавленной зоны таким образом, чтобы минимизировать общее время очистки.
-
Для заданных параметров получили:
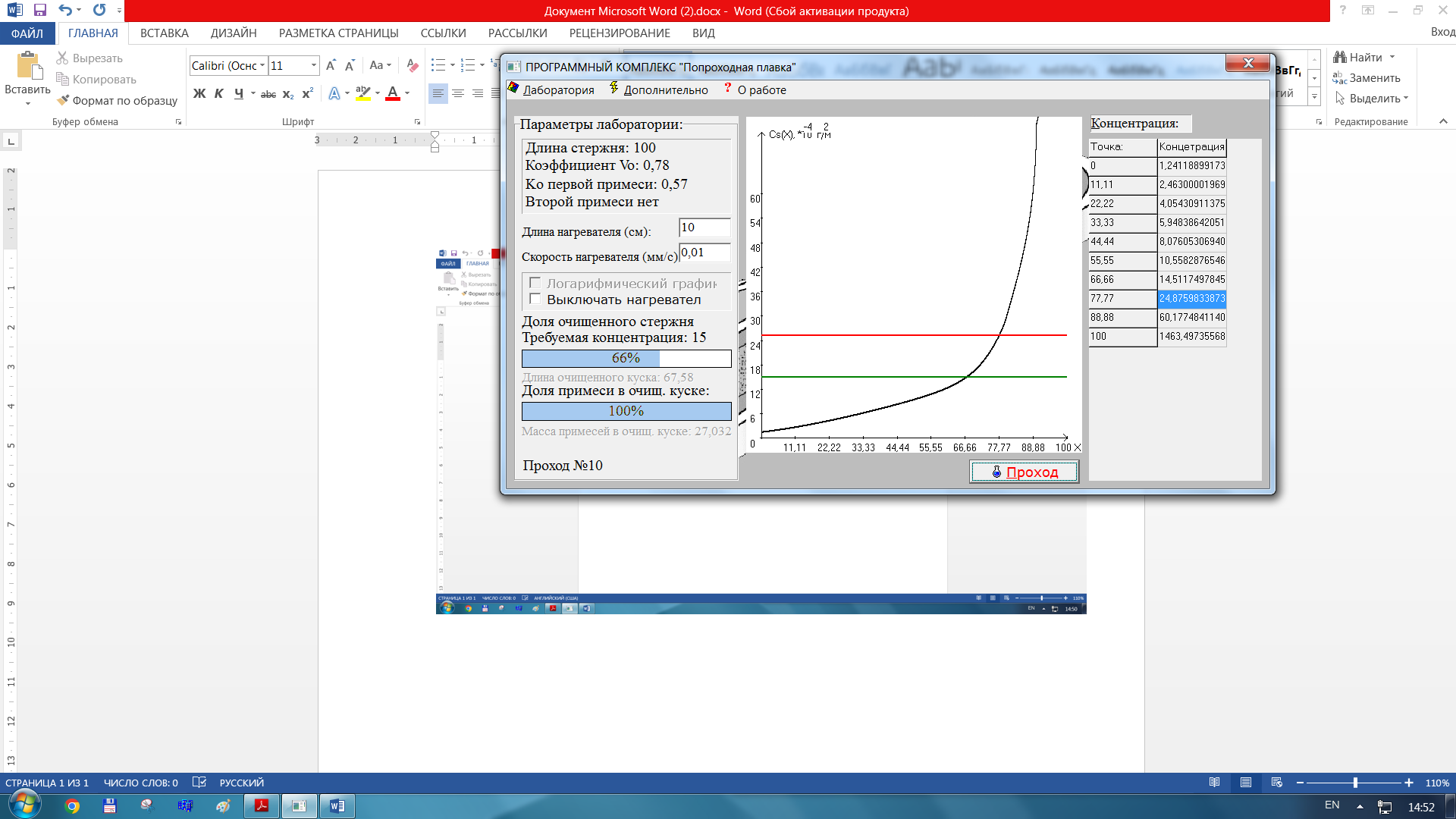
-
Изменив скорость нагревателя до 0,5 м/с получили следующие па -
раметры и результаты :
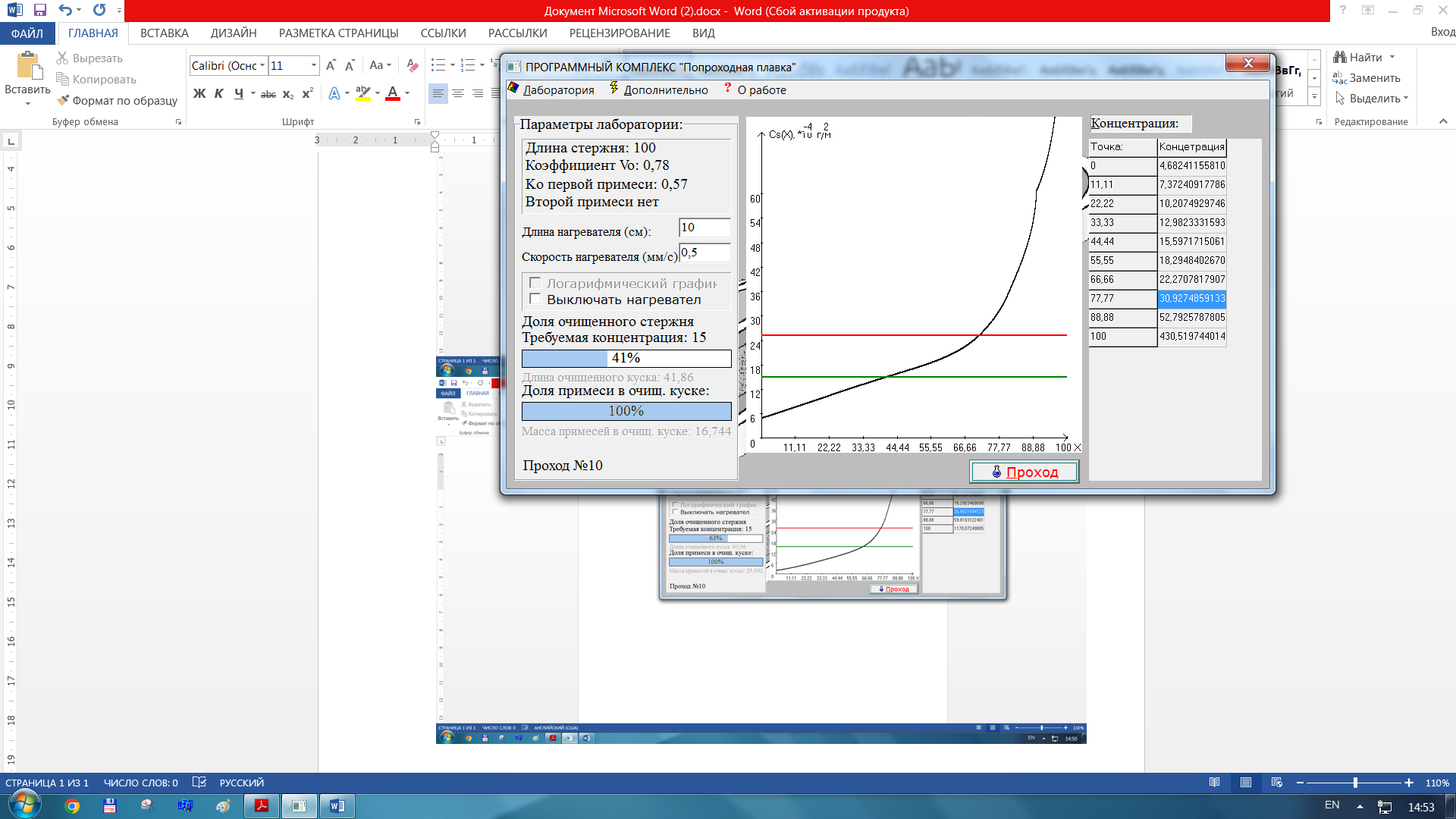
-
Изменив в параметрах плавки длину стержня получили следующие параметры и результаты на 10 проход:
-
Вернули длину стержня 100, скорость оставили такой же:
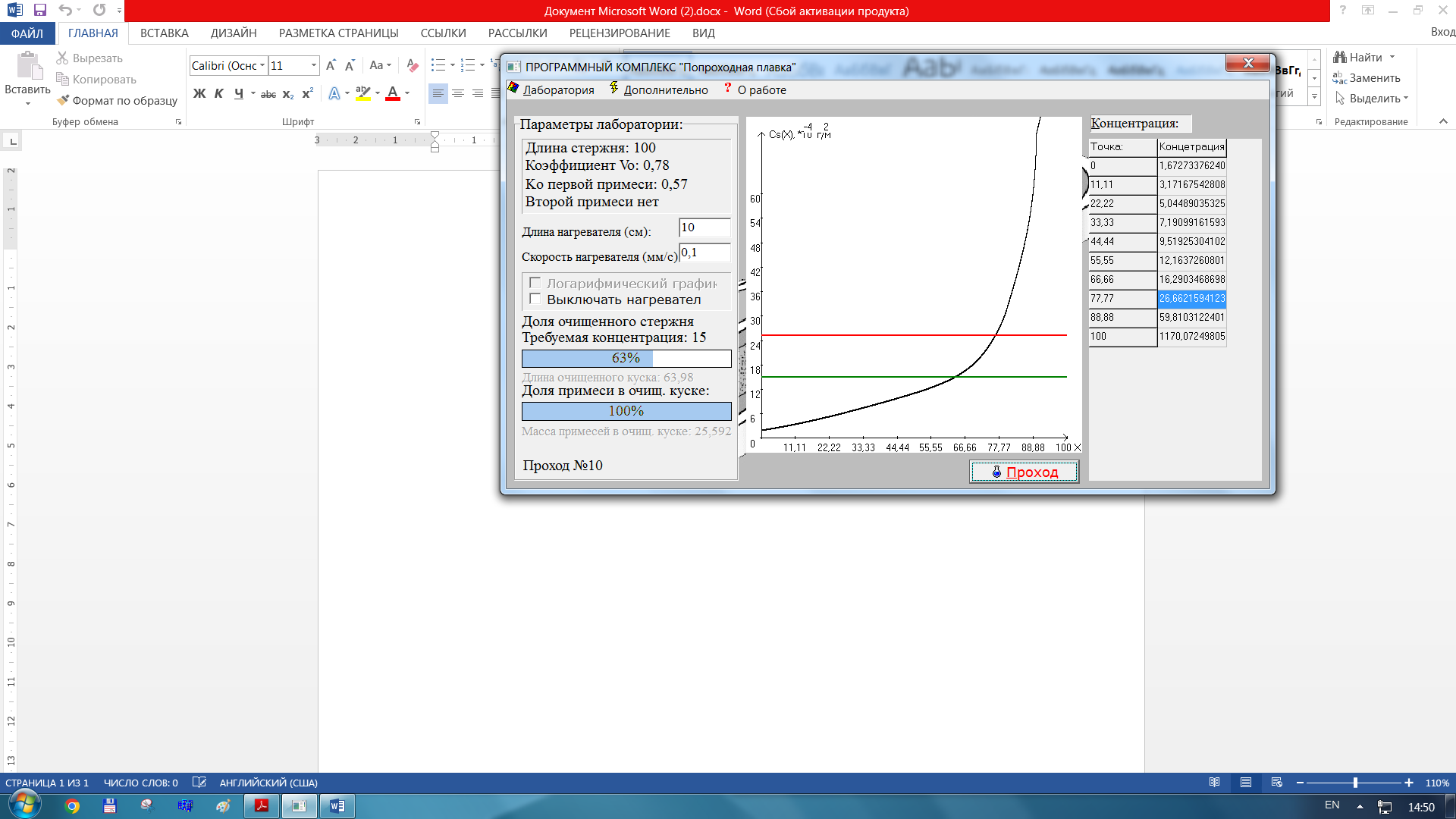
-
Таким же способом меняем параметры установки и получаем
-
Понизили параметр длинны стержня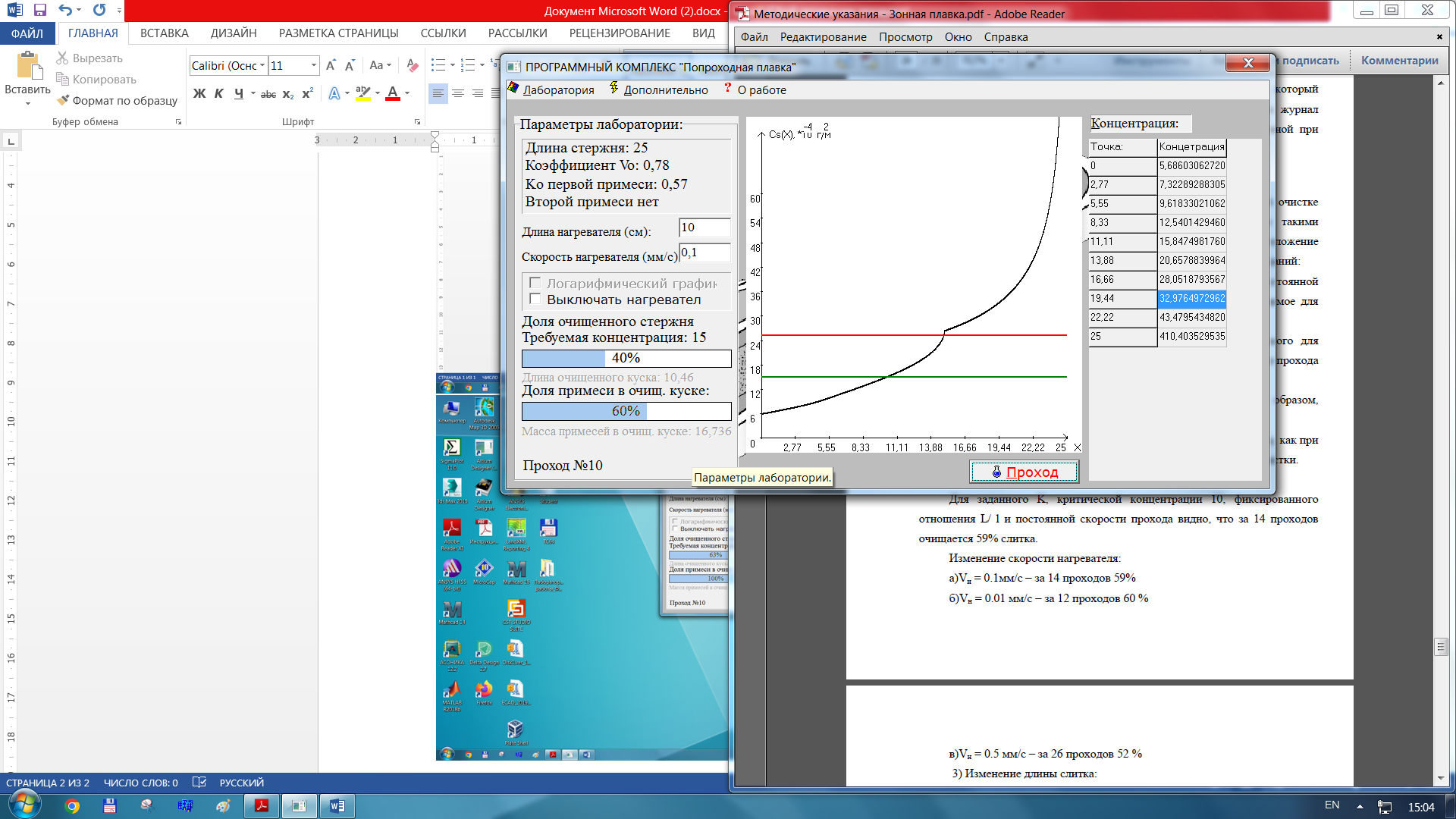
-
Изменяем коэф. первой примеси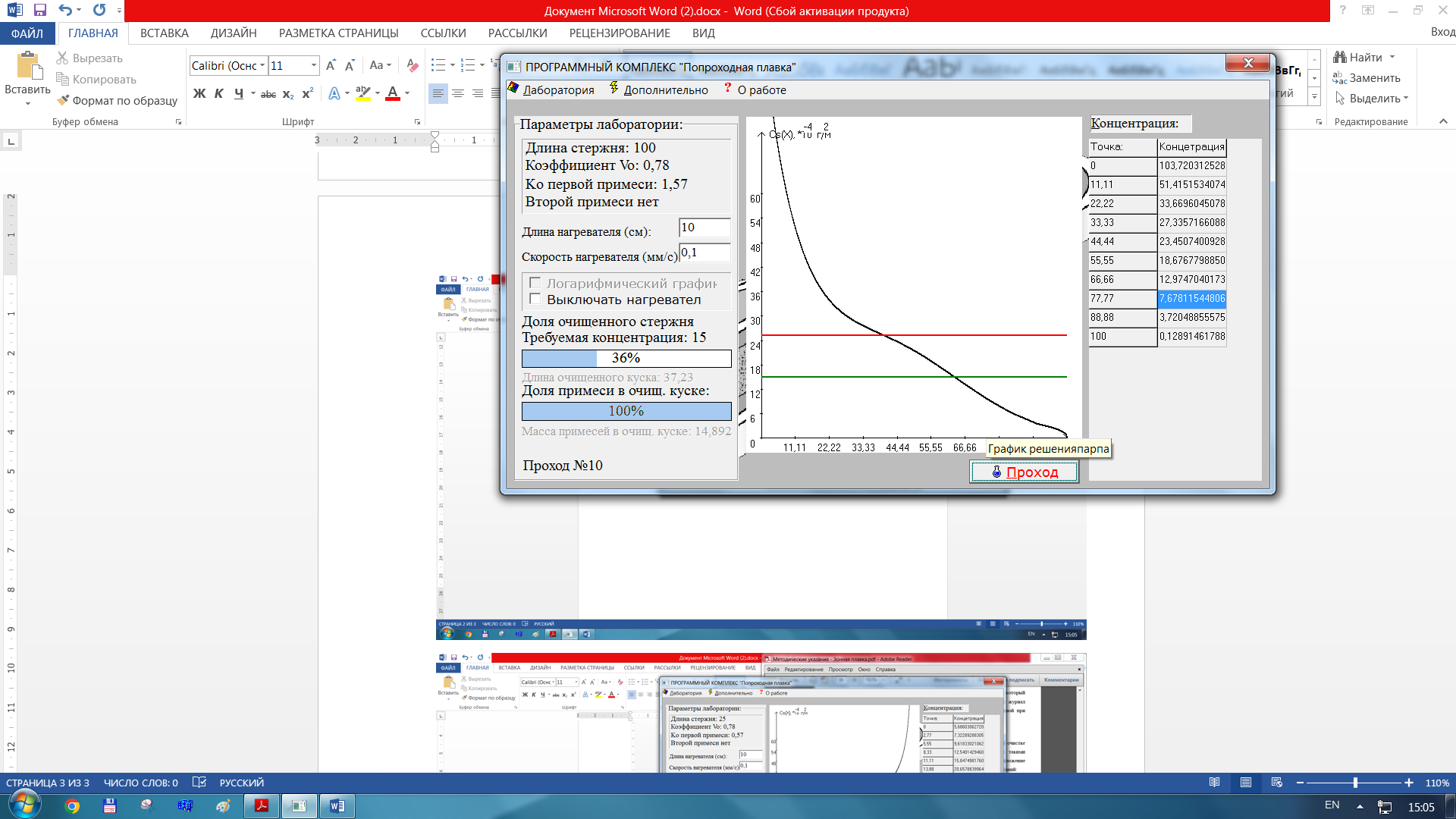
-
Уменьшаем скорость оставляя другие показатели
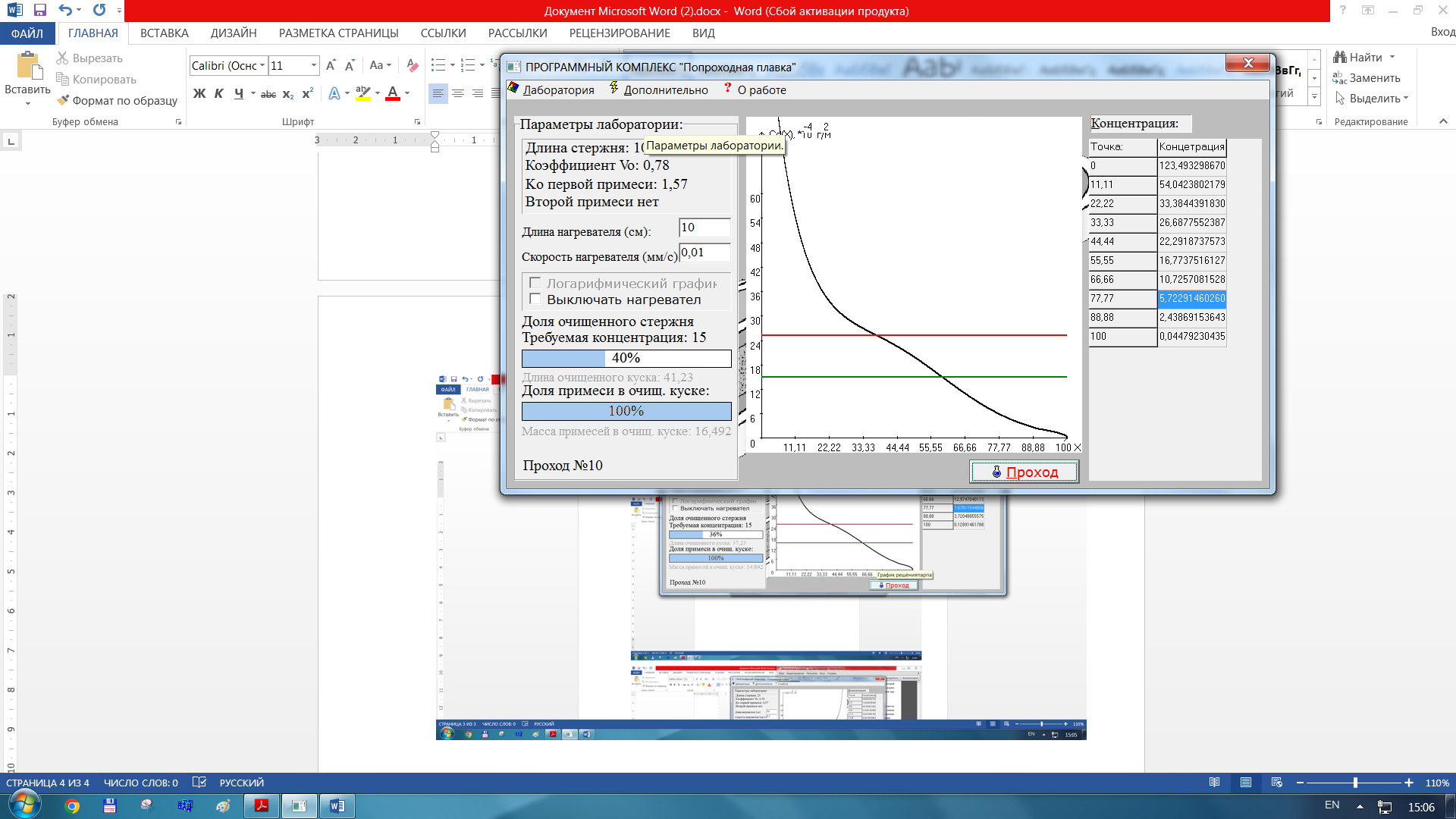
-
Увеличиваем скорость оставляя другие показатели
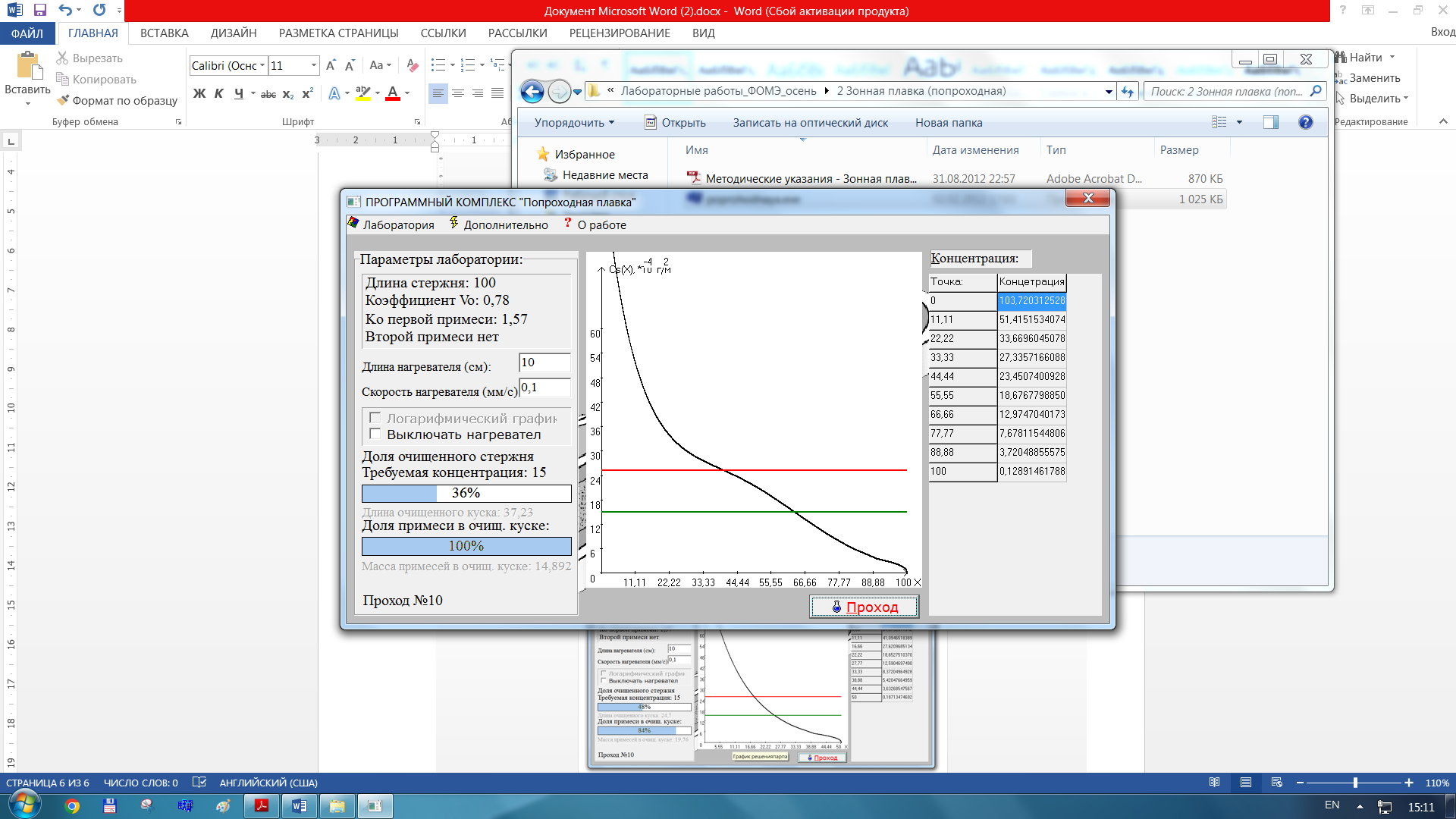
-
«Укоротили» стержень
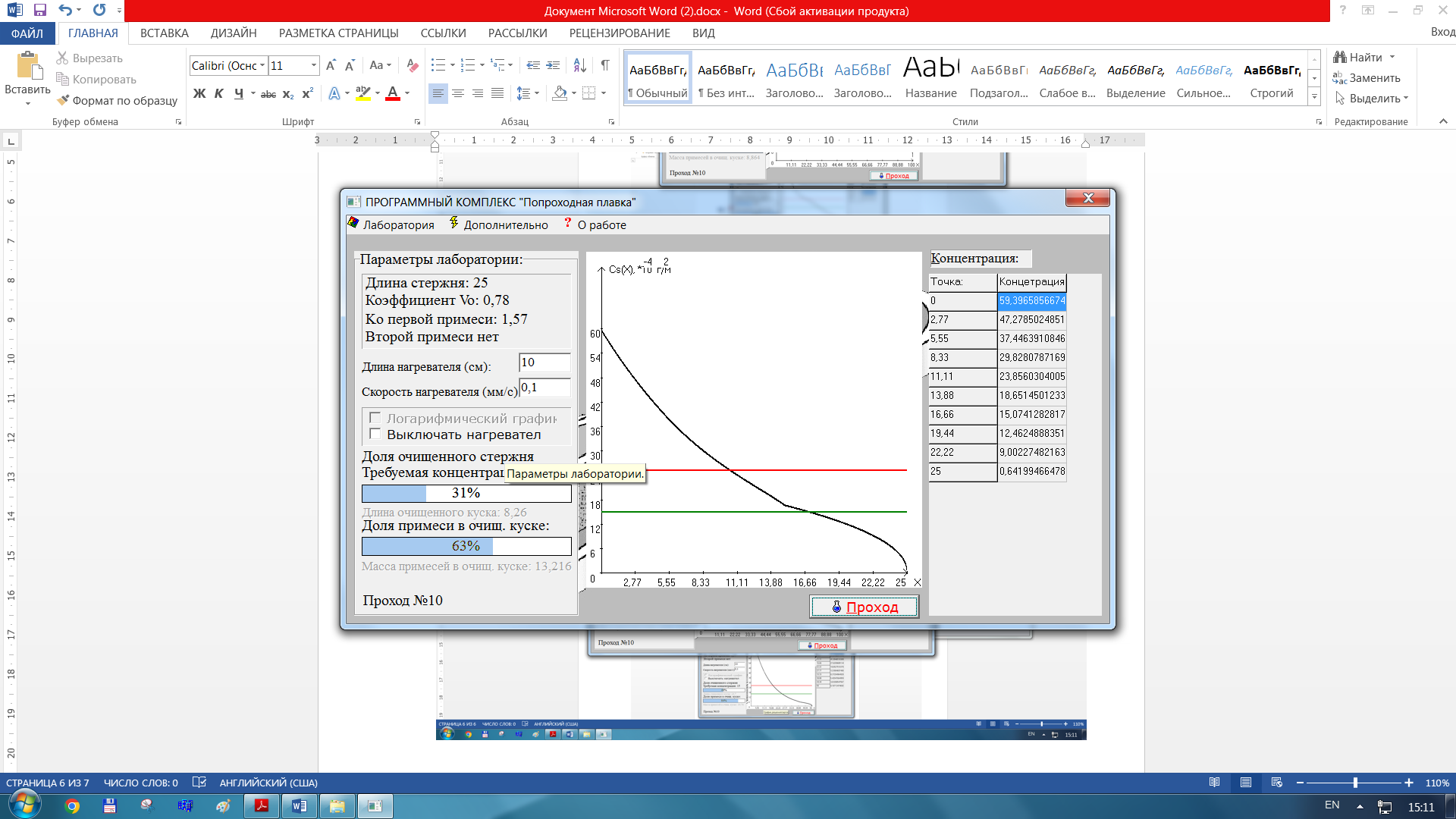
-
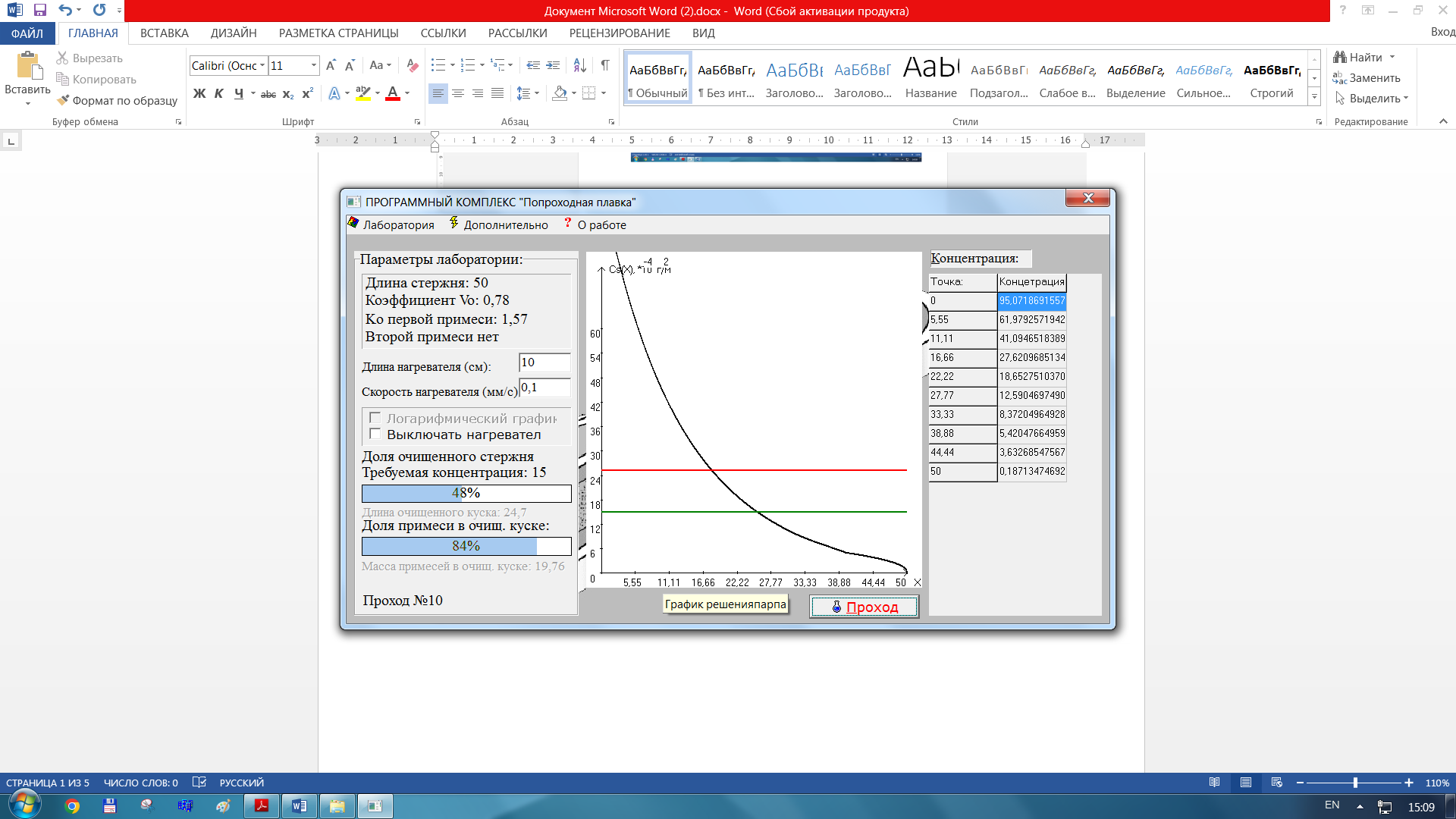
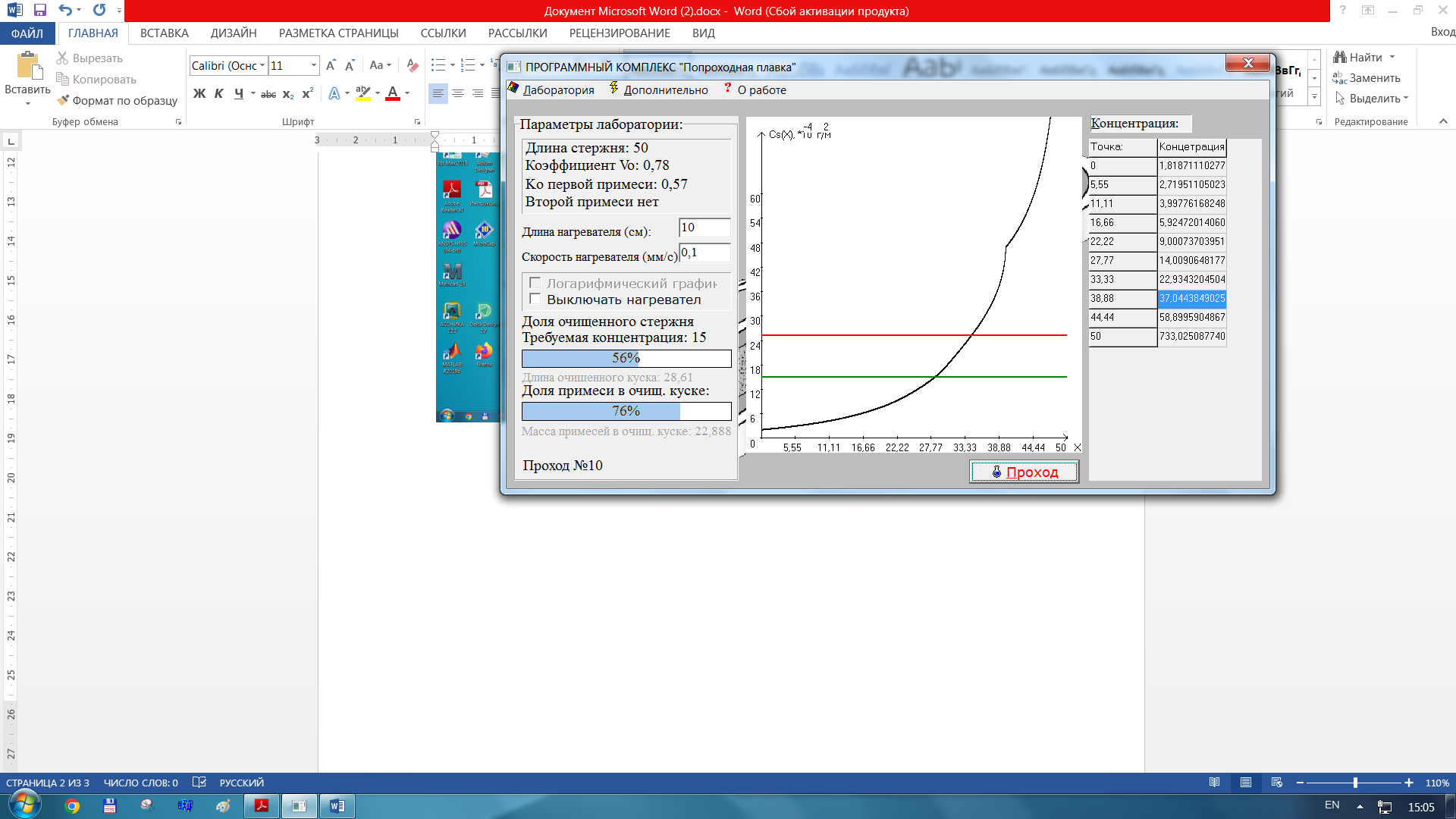
Результаты с измененной длинной стержня 50

На основе сделанных нами экспериментов сделаем вывод, как при изменении параметров можно добиться максимально возможной очистки.
Для K0 = 0.57 Для заданного K, критической концентрации 10, фиксированного отношения L/ l и постоянной скорости прохода видно, что за 14 проходов очищается 59% слитка.
Изменение скорости нагревателя:
a)Vн = 0.1мм/c – за 14 проходов 59%
б)Vн = 0.01 мм/с – за 12 проходов 60 %
в)Vн = 0.5 мм/с – за 26 проходов 52 %
3) Изменение длины слитка:
a)при L = 100 см – за 14 проходов 59 %
б)при L = 50 см – за 4 прохода 26 %
в)при L = 25 см – за 1 проход 10 %
Для K0 = 1.57: Для заданного K0, критической концентрации 10, фиксированного отношения L/ l и постоянной скорости прохода видно, что за 15 проходов очищается 41% слитка
Изменение скорости нагревателя:
a)Vн = 0.1мм/c – за 15 проходов 41 %
б)Vн = 0.01 мм/с – за 12 проходов 45 %
в)Vн = 0.5 мм/с – за 37 проходов 40 %
2) Изменение длины слитка:
a)при L = 100 см – за 15 проходов 41 %
б)при L = 50 см – за 4 прохода 20 %
в)при L = 25 см – за 1 проход 8 %
Следовательно, максимально возможный вариант очистки для K0 = 0.57 и K0 = 1.57 возможен при скорости прохода Vн = 0.01 мм/с. И следовательно, чем меньше слиток тем быстрее он очищается.
Выводы.
На основе нашего исследования сделали вывод о том как оперируя вводимыми параметрами, достичь максимально возможной очистки металла. Состояние включенного и выключенного нагревателя не влияет на очистку металла.
