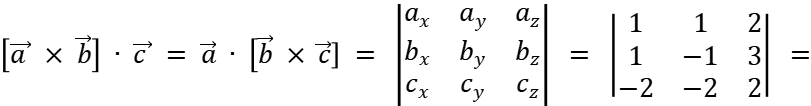Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ» Кафедра экономики и управления Форма обучения: заочная с ДОТ
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ Линейная алгебра
Группа М20Э111
Студент		А. Р. Валеева

МОСКВА 2021

1. 
   Найти сумму матриц
   

1. 
   
   

2. 
   
   

2. 
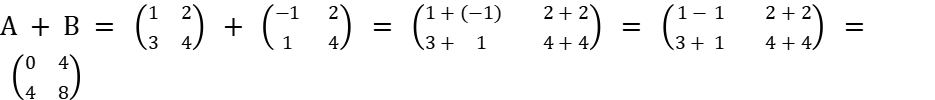
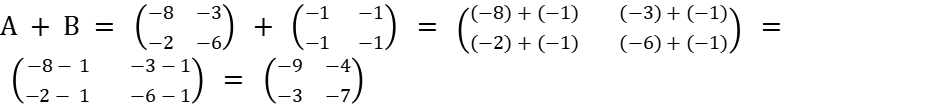
   Найти произведение матриц
   

2.1.


Компоненты матрицы С вычисляются следующим образом:

---

2.2.

Компоненты матрицы С вычисляются следующим образом:

3. 
   Найти определение матриц
   

3.1.


3.2.

4. 
   Решить систему уравнений
   

4.1.
Поделим 1-е уравнение на 7:

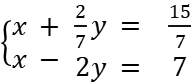
Из 1-го уравнения выразим х через остальные переменные:

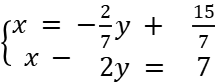
Во 2-е уравнение подставляем x:

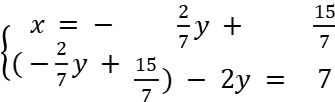
После упрощения получим:

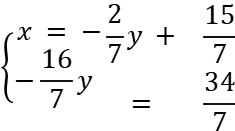
Теперь, двигаясь от послед. уравнения к первому, можно найти значения остальных переменных:


4.2.
Приведем сиситему уравнений к каноническомц виду:

Запишем систему лин. Уравнений в матричном виде:

---

- это ксть сиситема уравнений, имеющая форму A*x = B

Решение такого матричного уравнения методом Крамера найдём так:

Т.к. определитель матрицы:

, то

Корнеь xi получается делением определителя матрицы Ai. на определитель матрицы А. ( Ai получаем заменой в матрице А i - го столбца на столбец В )

5. 
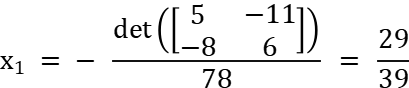
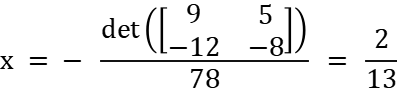
   Для заданных векторов найти смешанное произведение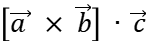
   

5.1.





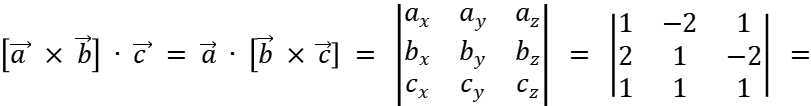
5.2.

---

Смотрите также файлы

• Имямодель Параметры.docx

• Бехтерев Владимир Михайлович.pdf

• Министерство здравоохранения Московской области Государственное бюджетное профессиональное образовательное учреждение.docx

• Презентация по дисциплинам мдк. 03. 01 Организация деятельности аптеки и её структурных подразделений.pptx

• Анализируйте национальный состав мигрантов за последние 3 год.docx