Файл: Решение Будем рассматривать совокупность условий как систему логических уравнений, каждое из которых является истинным (1).doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.03.2024
Просмотров: 5
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание.
Сколько существует различных наборов значений логических переменных
, которые удовлетворяют всем перечисленным условиям?
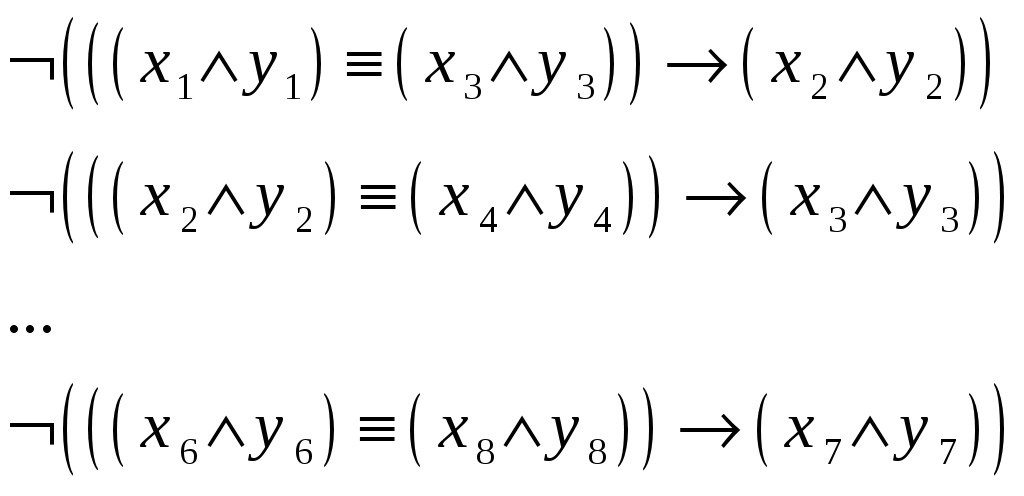
Решение
Будем рассматривать совокупность условий как систему логических уравнений, каждое из которых является истинным (=1):
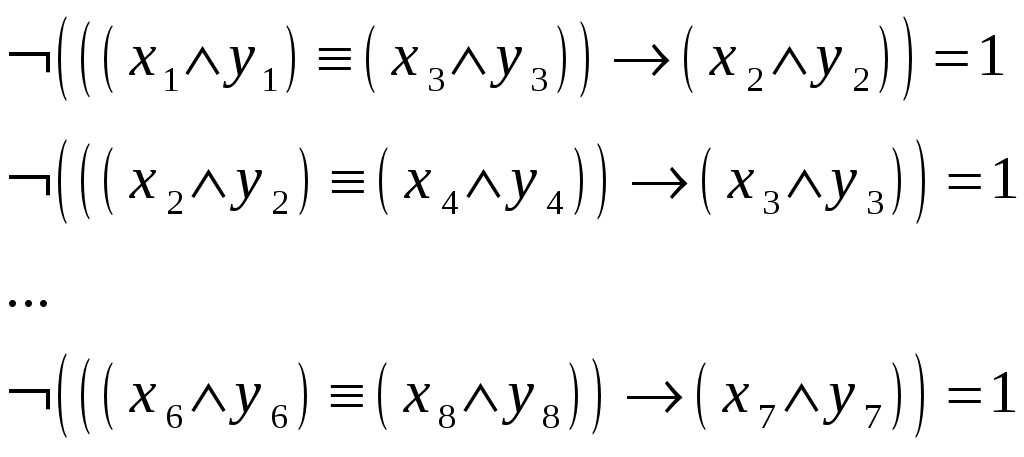
Упростим выражения с учетом того, что в левой части находится отрицание выражения. Применим отрицание к обеим частям и к левой – закон двойного отрицания. Получим:
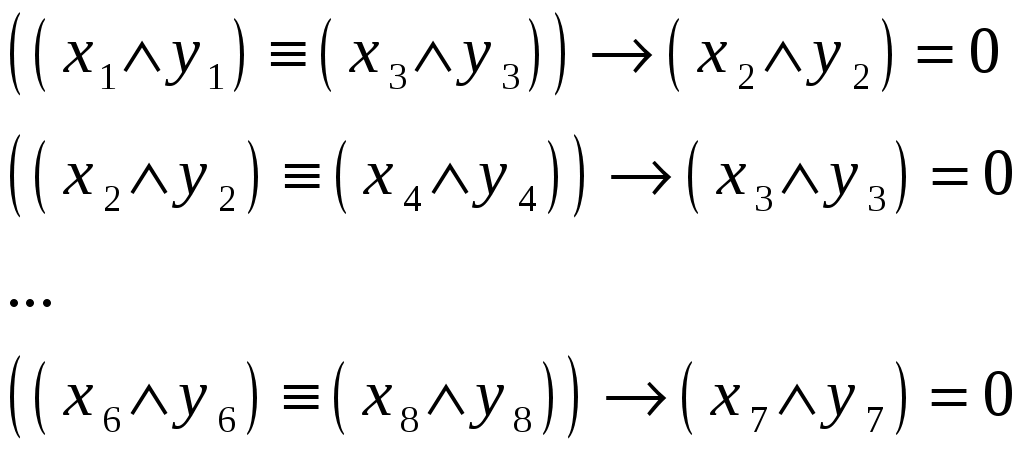
Заметим, что выражения состоят из однотипных конъюнкций, причем каждая переменная входит только в одно выражение. Для упрощения уравнений введем новые переменные:
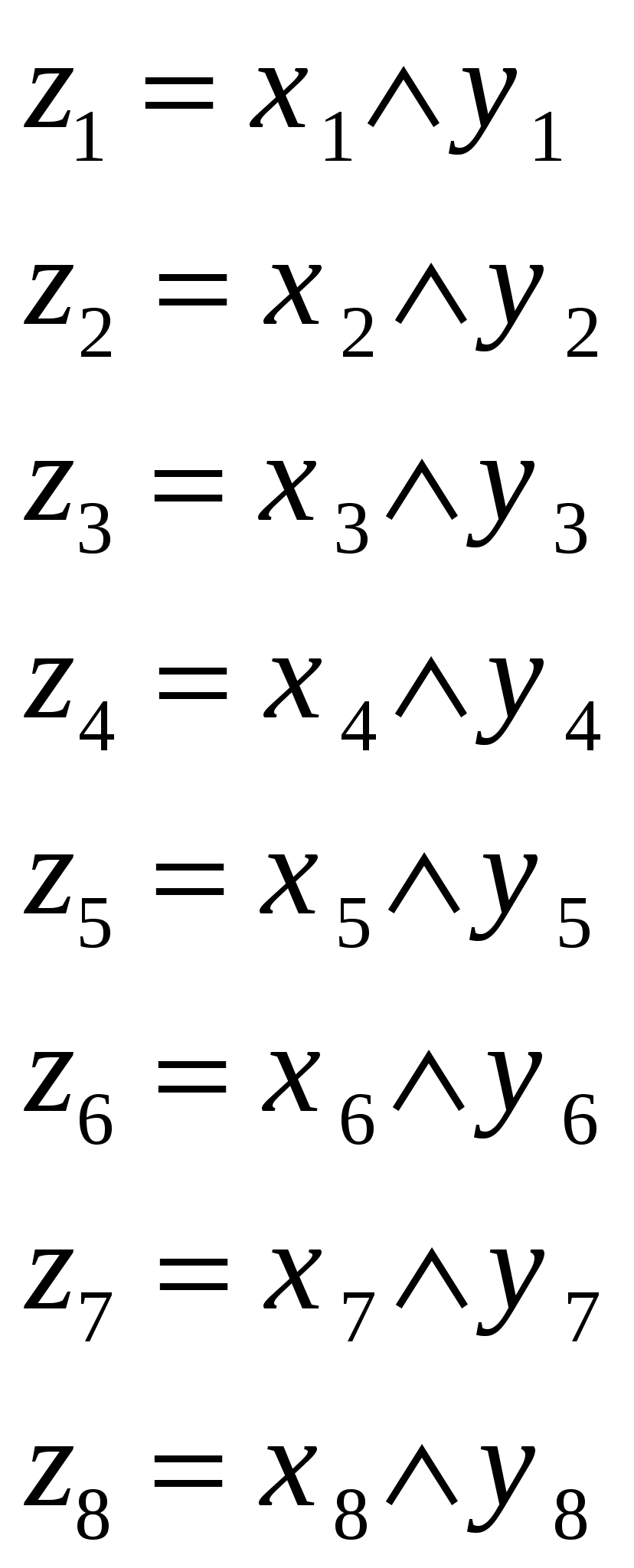
Тогда систему можно записать в виде:
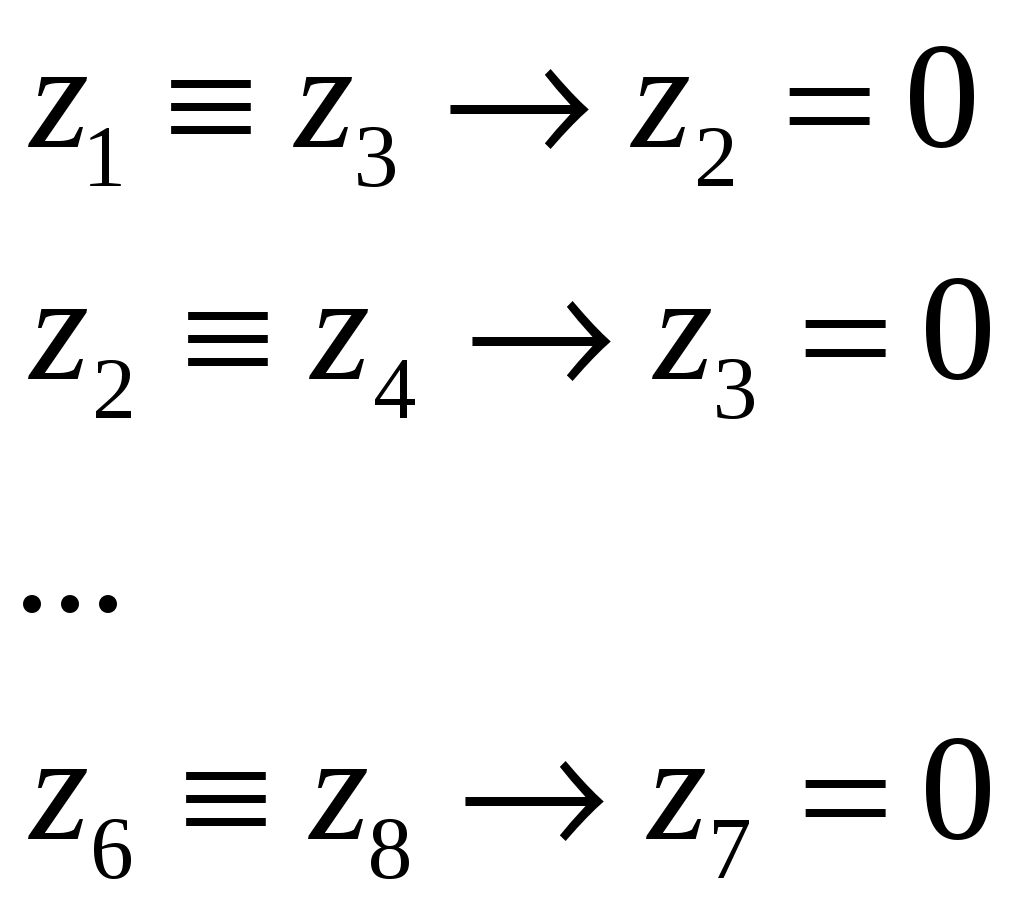
Решим первое уравнение, составив таблицу истинности выражения из левой части
-
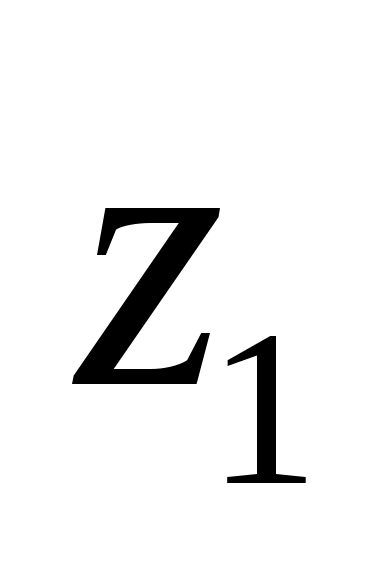
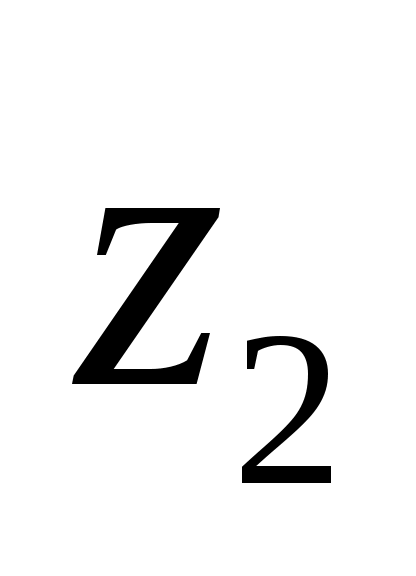
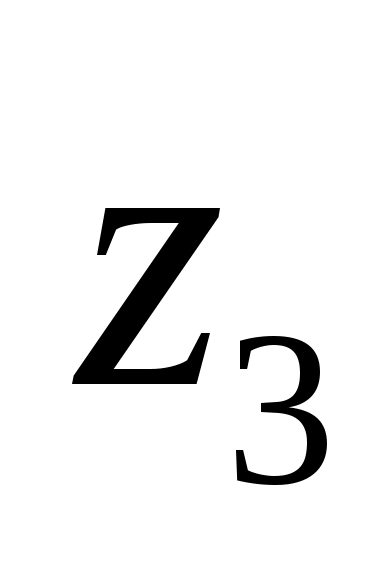
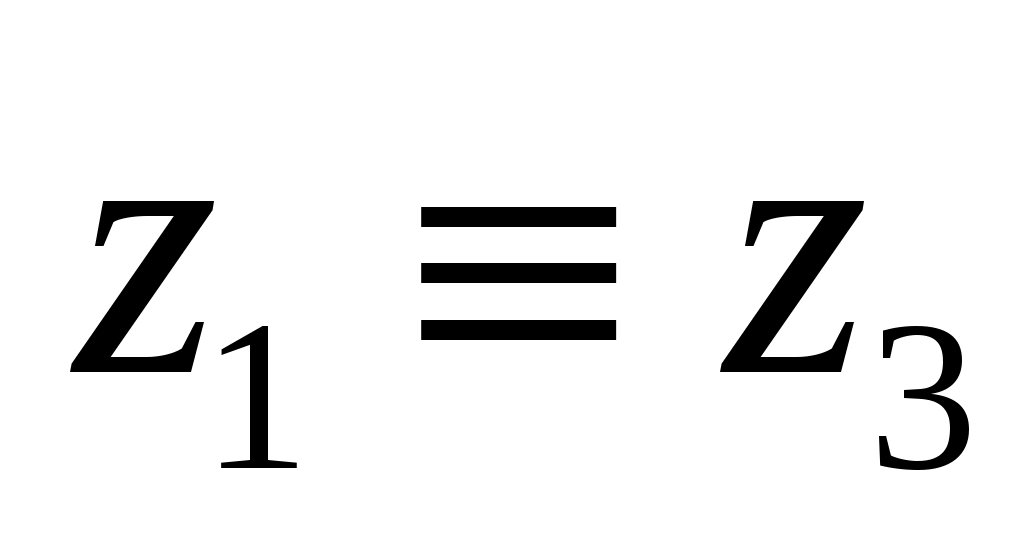
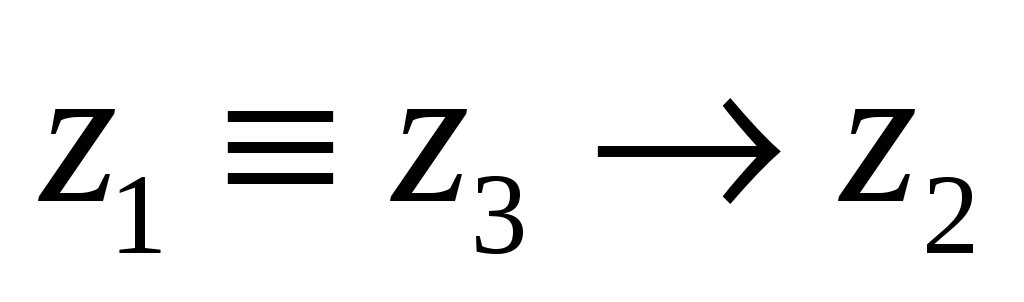
0
0
0
1
0
0
0
1
0
1
0
1
0
1
1
0
1
1
0
1
1
0
0
0
1
1
0
1
1
0
1
1
0
0
1
1
1
1
1
1
Первое уравнение имеет 2 решения (выделены в таблице желтым цветом).
Рассмотрим, что происходит с этими решениями на примере уравнения 2 (переменная
во втором уравнении не участвует, но в системе она присутствует, поэтому выделена другим цветом).-
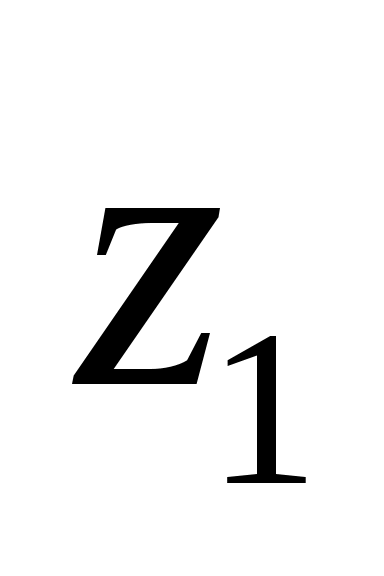
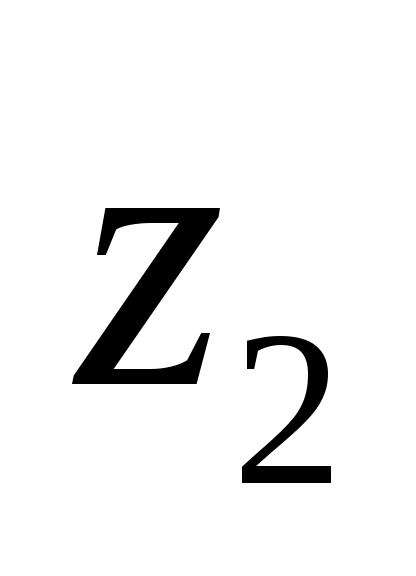
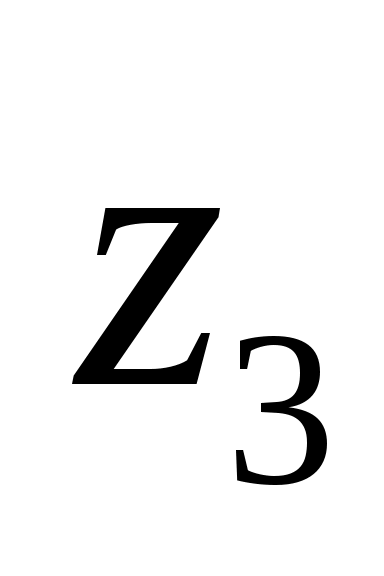
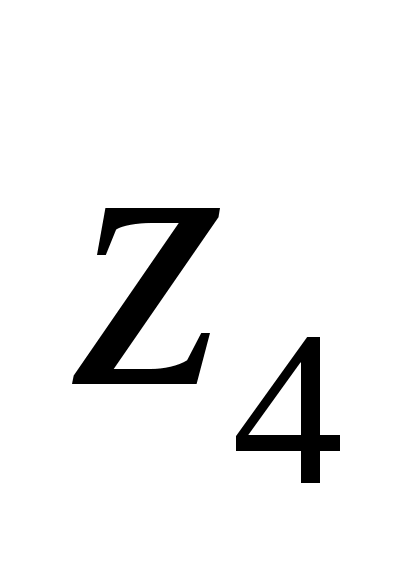
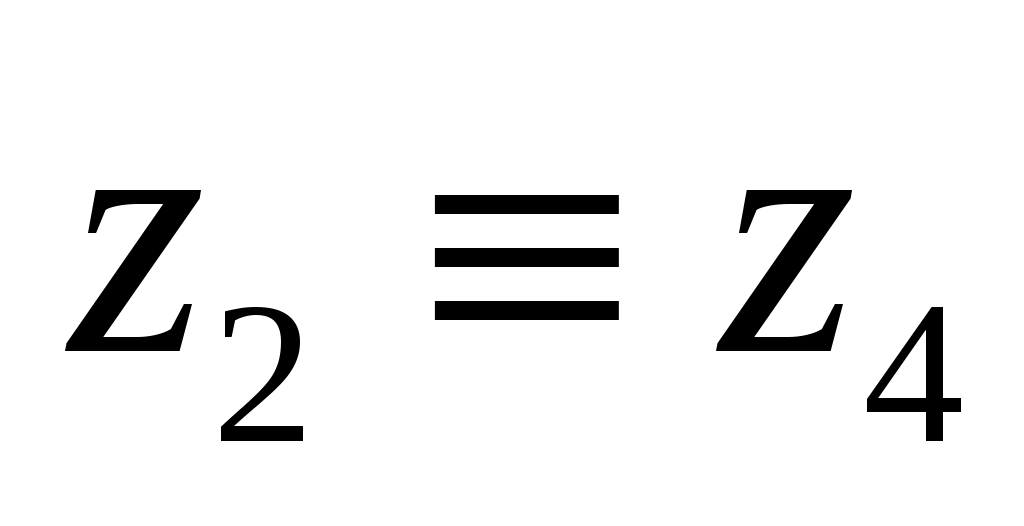
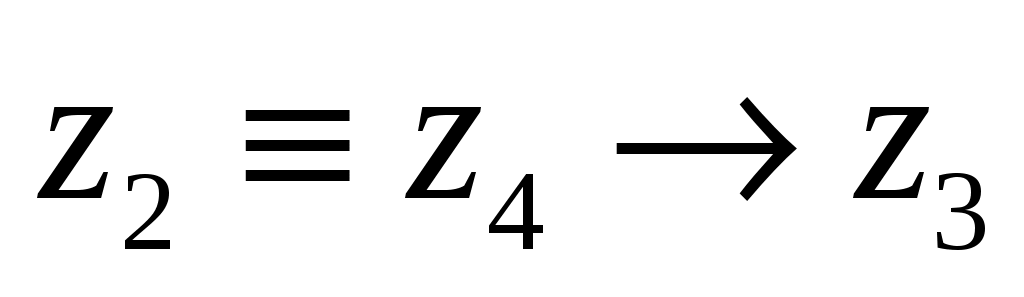
0
0
0
1
0
1
0
1
0
Так как правая часть равна 0 (ЛОЖЬ), то получить мы это можем для импликации в единственном случае
, т. е для первой строки при известном 
должно выполняться равенство . Так как значение 
известно из решения первого уравнения, понятно, что для возможно единственное значение 
.Рассмотрим вторую строку. Это импликация
, которая должна быть равна 0 (ЛОЖЬ). Но в данном случае это невозможно, так как 
, значит, при любых значениях выражения 
импликация будет равна 1 (ИСТИНА).Значит, система из первых двух уравнений имеет единственное решение.
-
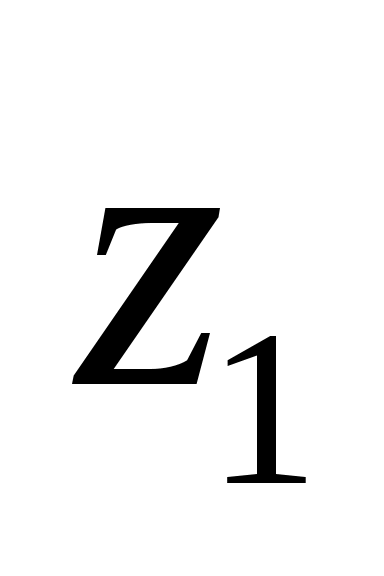
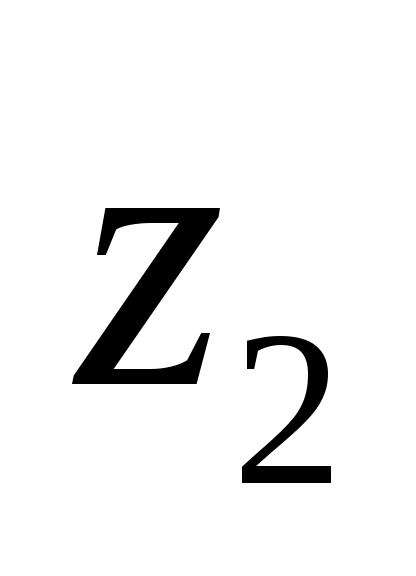
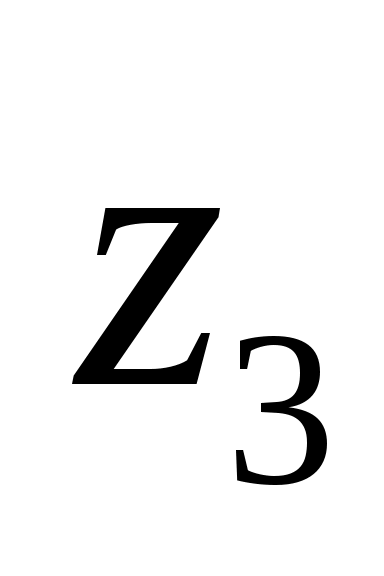
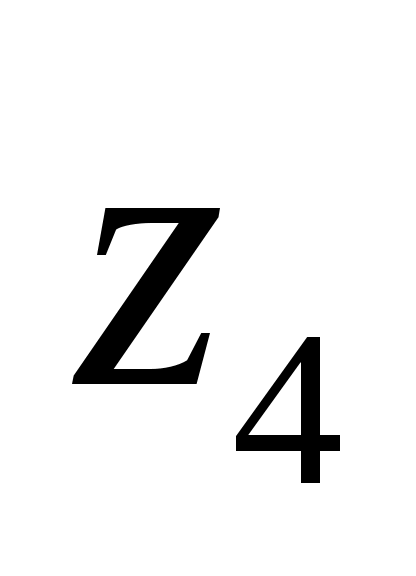
0
0
0
0
Рассуждая аналогично и анализируя условие системы
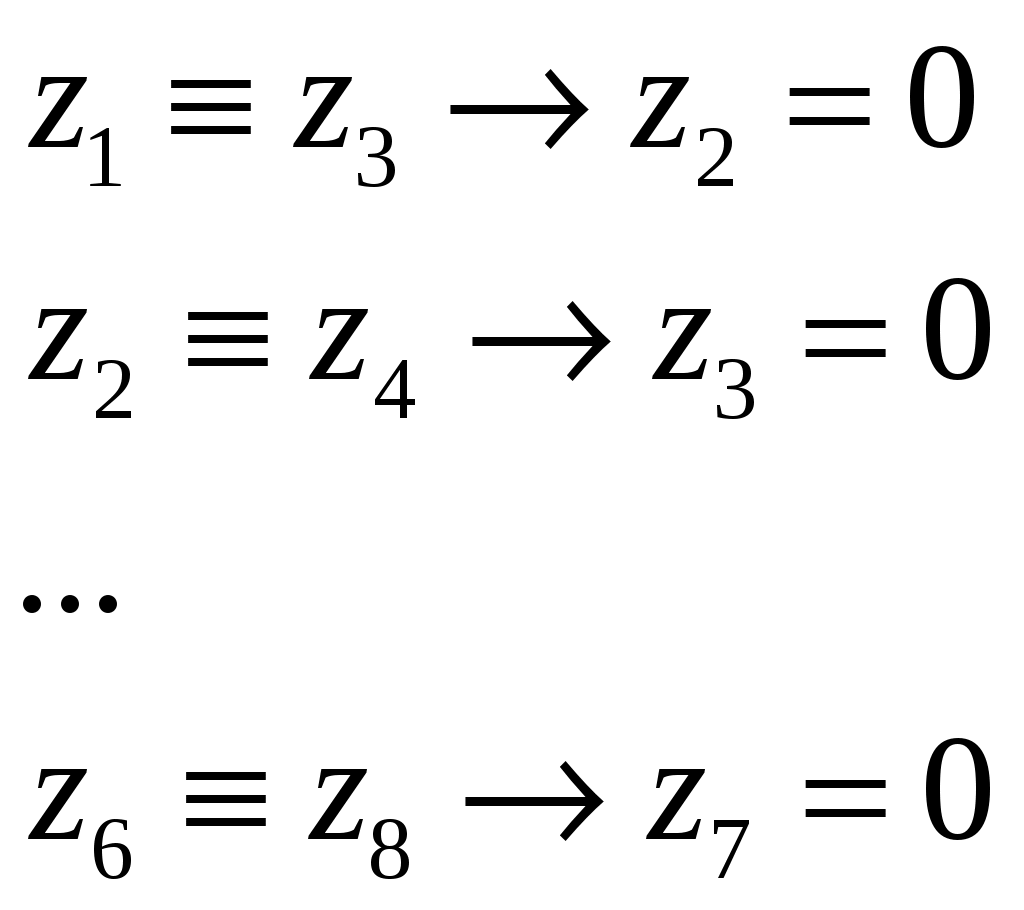,получим, что данная система может иметь только единственное решение, в котором значения всех логических переменных равны 0 (ЛОЖЬ):
-
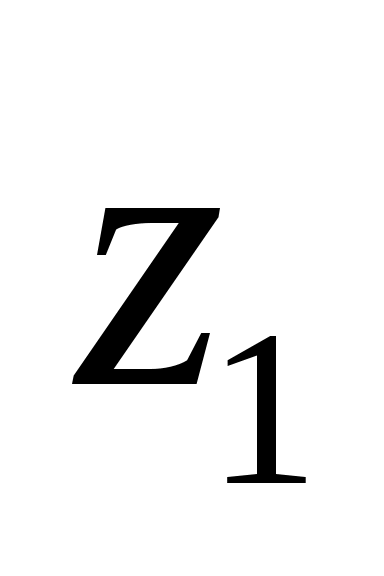
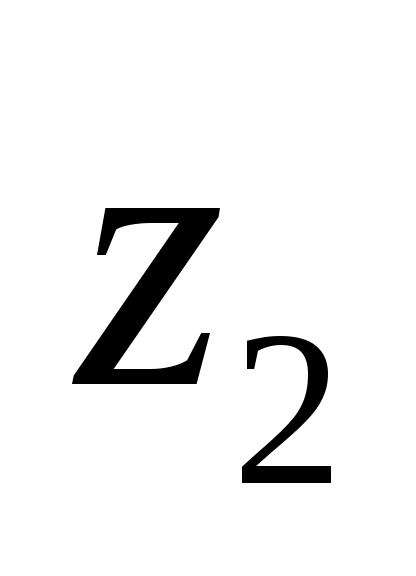
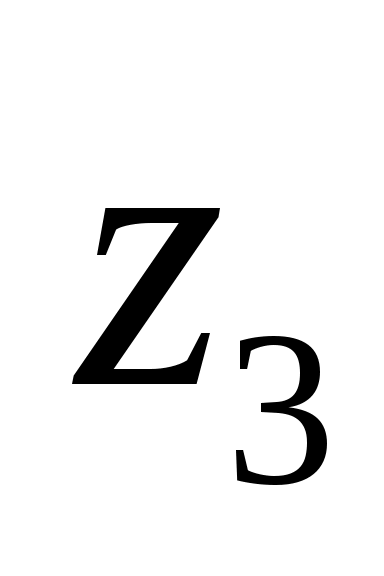
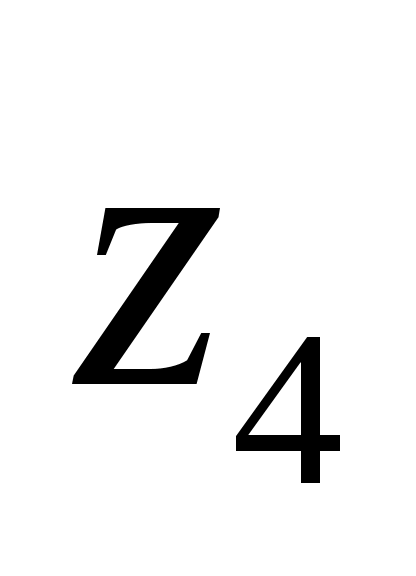
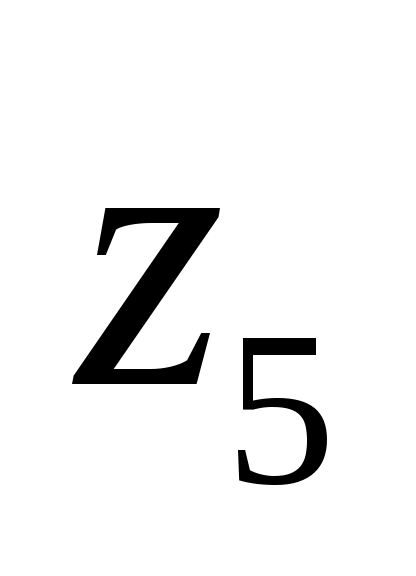
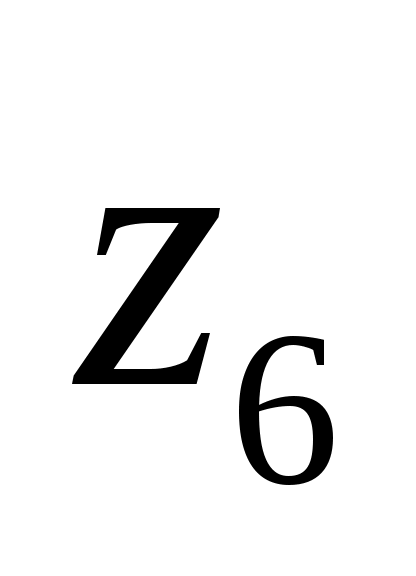
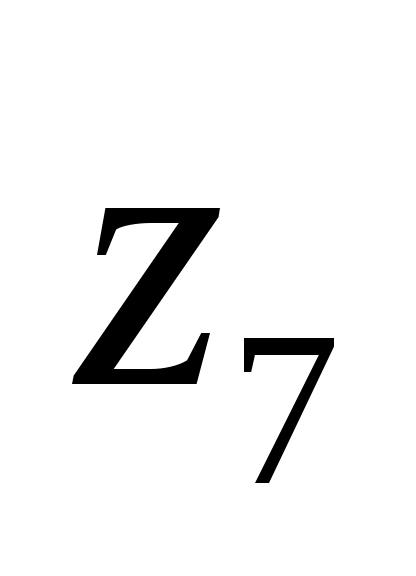
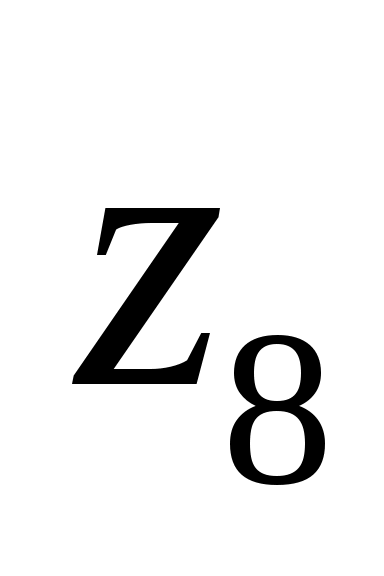
0
0
0
0
0
0
0
0
Перейдем к исходным обозначениям. Для этого выясним, сколько нулевых и сколько единичных значений дает каждая введенная переменная
. Так как переменные однотипны, рассмотрим только первую.
-
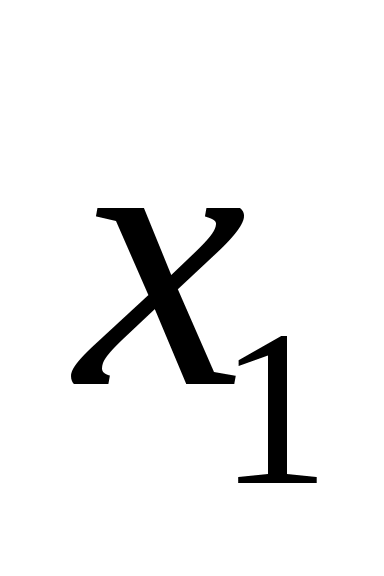
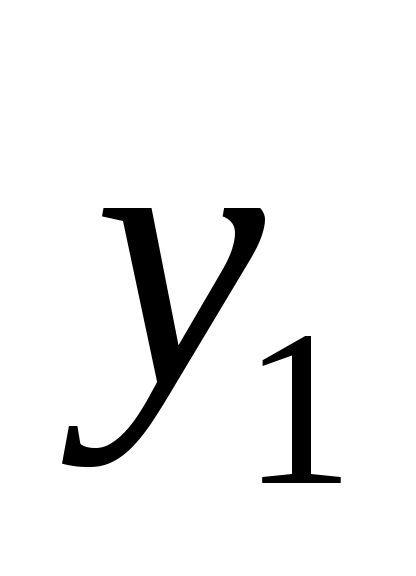
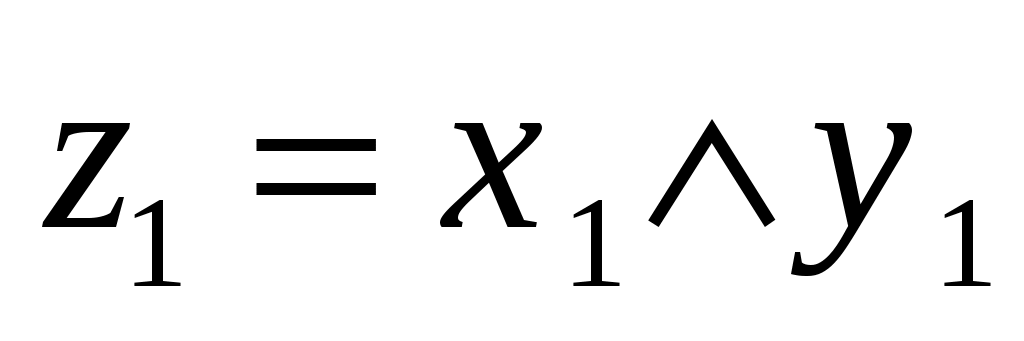
0
0
0
0
1
0
1
0
0
1
1
1
В трех случаях переменная z равна 0, значит, в таблице под каждым решением, где
, мы подпишем 3 – такое количество решений в исходных обозначениях даст каждый 0.-
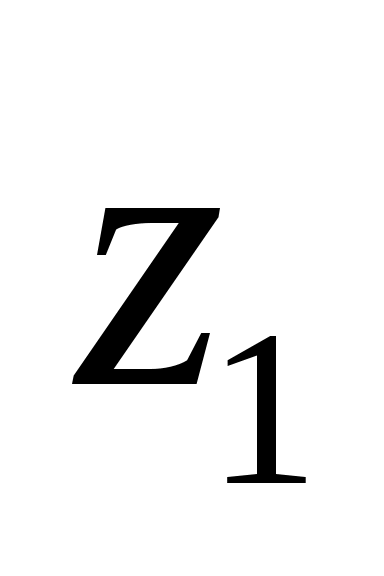
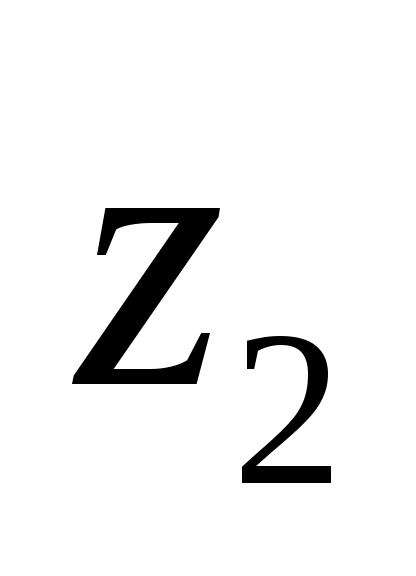
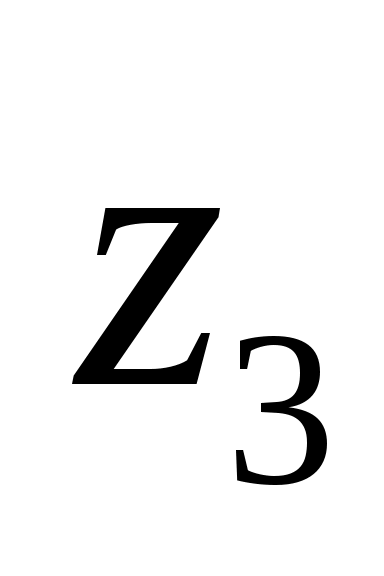
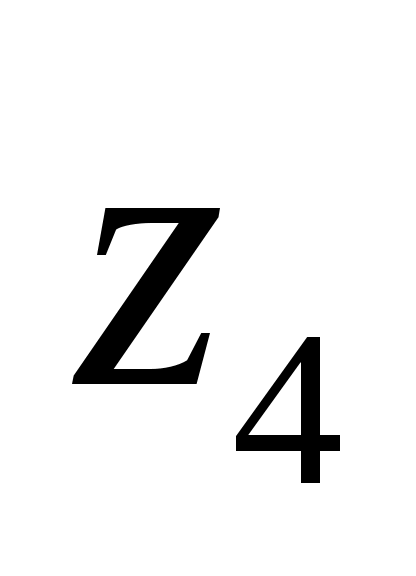
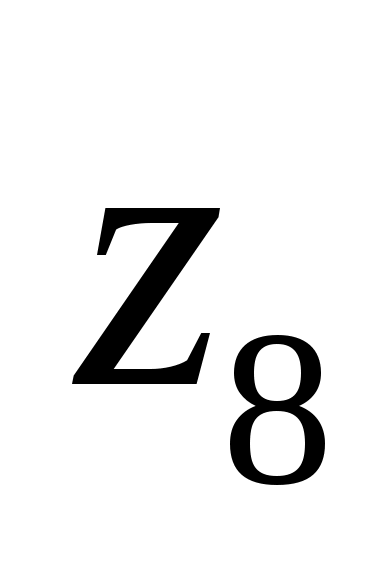
0
0
0
0
0
0
0
0
3
3
3
3
3
3
3
3
Теперь, чтобы получить решение исходной задачи, надо перемножить все числа в последней строке:
Различных наборов значений логических переменных
, которые удовлетворяют всем перечисленным условиям
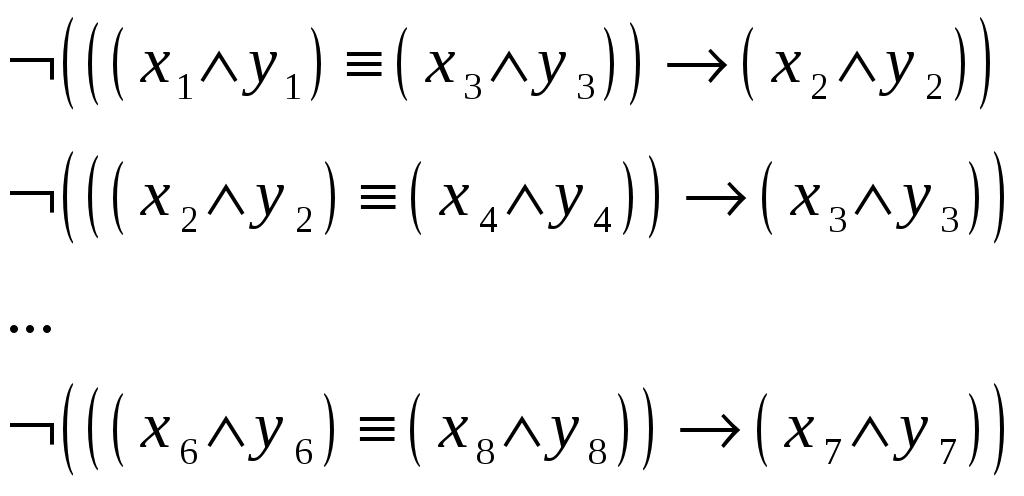
существует 6561.
Ответ: 6561