ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.03.2024
Просмотров: 33
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Пример 2. Найти оптимальный план поставок, используя первоначальный план поставок (таблица 1) и матрицу оценок этого плана

 0 5 −1 −4
0 5 −1 −4
0 0 0
1 4 0
−2 .
0
Решение. Поскольку матрица оценок первоначального плана поставок
содержит отрицательные числа, то этот план является неоптимальным. Проведём его оптимизацию распределительным методом.
Шаг 1. Необходимо выбрать клетку с наименьшей оценкой. В представленной матрице такой клеткой является клетка (1,4). Ее оценка равна минус четыре.
Шаг 2. Необходимо построить первый цикл пересчета. Для этого надо, начиная с клетки (1,4), двигаться только по отмеченным клеткам и вернуться в клетку (1,4). При этом запрещается делать два последовательных шага в одной строке или в одном столбце.
Например, используем такой цикл пересчета: (1,4)(3,4)(3,3)(2,3)(2,1)(1,1)(1,4).
Стартовой клетке цикла присваивается знак «+». Двигаясь по циклу знаки клеток чередуются. На рис. 1 представлен цикл пересчета. Для каждой клетки указаны индекс, объем поставок и присвоенный знак.
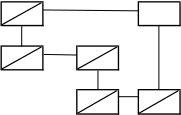
Рис. 1. Цикл пересчета на первой итерации Среди клеток, отмеченных знаком «» (клетки (3,4); (2,3); (1,1)),
выберем минимальную величину поставки: min (130, 30, 30) = 30. Далее во всех клетках со знаком «» уменьшим поставки на этот минимум, а
в клетках со знаком «+» увеличим на этот минимум. Клетка (1,4) становится отмеченной. Если после такого пересчета получается одна клетка с нулевой поставкой, то она становится пустой. В нашем случае таких клеток две (1,1) и (2,3). Клетку с наибольшим тарифом переводим в разряд пустых это клетка (1,1). В клетке (2,3) останется нулевой объем поставки, но она останется отмеченной. Напомним, что должно соблюдаться правило: число отмеченных клеток равняется сумме чисел
строк и столбцов минус единица. Получен новый план поставок (таблица 3). Необходимо всегда осуществлять проверку нового плана поставок: сумма поставок по строкам должна равняться спросу потребителя, а по столбцам мощностям поставщиков.
 Таблица 3
Таблица 3
Шаг 3. Находим матрицу оценок для нового плана поставок

 4 9 3 0
4 9 3 0
0 0 0
1 4 0
−2 .
0
Первая итерация закончилась. Полученная матрица оценок указывает
на то, что и новый план поставок является неоптимальным. Возвращаемся к шагу 1.
Шаг 1’. Выбираем клетку (2,4).
Шаг 2’. Цикл пересчета: (2,4) (3,4) (3,3) (2,3) (2,4),
представлен на рис. 2.

Рис. 2. Цикл пересчета на второй итерации Минимальная величина поставки среди клеток со знаком «»: min (0,

 0 5 −1 −4
0 5 −1 −40 0 0
1 4 0
−2 .
0
Решение. Поскольку матрица оценок первоначального плана поставок
содержит отрицательные числа, то этот план является неоптимальным. Проведём его оптимизацию распределительным методом.
Шаг 1. Необходимо выбрать клетку с наименьшей оценкой. В представленной матрице такой клеткой является клетка (1,4). Ее оценка равна минус четыре.
Шаг 2. Необходимо построить первый цикл пересчета. Для этого надо, начиная с клетки (1,4), двигаться только по отмеченным клеткам и вернуться в клетку (1,4). При этом запрещается делать два последовательных шага в одной строке или в одном столбце.
Например, используем такой цикл пересчета: (1,4)(3,4)(3,3)(2,3)(2,1)(1,1)(1,4).
Стартовой клетке цикла присваивается знак «+». Двигаясь по циклу знаки клеток чередуются. На рис. 1 представлен цикл пересчета. Для каждой клетки указаны индекс, объем поставок и присвоенный знак.

Рис. 1. Цикл пересчета на первой итерации Среди клеток, отмеченных знаком «» (клетки (3,4); (2,3); (1,1)),
выберем минимальную величину поставки: min (130, 30, 30) = 30. Далее во всех клетках со знаком «» уменьшим поставки на этот минимум, а
в клетках со знаком «+» увеличим на этот минимум. Клетка (1,4) становится отмеченной. Если после такого пересчета получается одна клетка с нулевой поставкой, то она становится пустой. В нашем случае таких клеток две (1,1) и (2,3). Клетку с наибольшим тарифом переводим в разряд пустых это клетка (1,1). В клетке (2,3) останется нулевой объем поставки, но она останется отмеченной. Напомним, что должно соблюдаться правило: число отмеченных клеток равняется сумме чисел
строк и столбцов минус единица. Получен новый план поставок (таблица 3). Необходимо всегда осуществлять проверку нового плана поставок: сумма поставок по строкам должна равняться спросу потребителя, а по столбцам мощностям поставщиков.
 Таблица 3
Таблица 3| | 70 | 120 | 150 | 130 | | |||||||
| 30 | 4 | 7 | 2 | 3 | 30 | 0 | ||||||
| 190 | 3 | | | 1 | | 2 | | 4 | -3 | |||
| | | 70 | | 120 | | 0 | ||||||
| 250 | 5 | 6 | 3 | | 7 | | -4 | |||||
| | 150 | | 100 | |||||||||
| | 0 | 2 | 1 | -‐3 | | |||||||
Шаг 3. Находим матрицу оценок для нового плана поставок

 4 9 3 0
4 9 3 00 0 0
1 4 0
−2 .
0
Первая итерация закончилась. Полученная матрица оценок указывает
на то, что и новый план поставок является неоптимальным. Возвращаемся к шагу 1.
Шаг 1’. Выбираем клетку (2,4).
Шаг 2’. Цикл пересчета: (2,4) (3,4) (3,3) (2,3) (2,4),
представлен на рис. 2.

Рис. 2. Цикл пересчета на второй итерации Минимальная величина поставки среди клеток со знаком «»: min (0,
