Файл: Подобные фигуры и их свойства. Признаки подобия треугольников.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.03.2024
Просмотров: 8
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Раздел: | Преобразования плоскости | |
| ФИО педагога | | |
| Дата: | 8.12.2022 | |
| Класс: 9А | Количество присутствующих: | Количество отсутствующих: |
| Тема урока | Подобные фигуры и их свойства. Признаки подобия треугольников. | |
| Цели обучения в соответствии с учебной программой | 9.1.4.16 знать и применять свойство биссектрисы треугольника | |
| Цели урока | -распознавать подобные фигуры; -применять свойства биссектрисы треугольника при решении задач. | |
Ход урока
| Этап урока | Действия педагога | Действия ученика | Оценивание | Ресурсы |
| Организационный этап | Приветствует учащихся, организует рабочее место. -Тех, кто готов работу начать Улыбки свои я прошу показать! Все готовы? Тогда повторяем, Систематизируем, изучаем и обобщаем, ИТАК, НАЧИНАЕМ! -Давайте улыбнёмся друг другу и с хорошим настроением начнём наш урок. Хочу начать сегодняшний урок со слов Лобочевского: «Математика - это язык, на котором говорят все точные науки.» (Н.И. Лобачевский) | Приветствуют учителя, организуют свое рабочее место, демонстрируют готовность к уроку. | | Диалогическое обучение Саморегулируемое обучение Критическое мышление Слайды 1-3 |
| Активизация опорных знаний | Проверка выполнения д/з Проверить домашнее задание учеников и обсудить задания, которые ученики не смогли решить. | Сверяют решение. Задают вопросы. | ФО: взаимное оценивание по критериям, комментарии учителя | |
| Изучение нового материала | Работа в парах. Практическая работа. Разобрать новый материал, сделать конспект в тетради:
 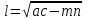 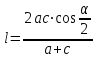 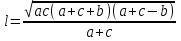
 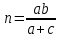
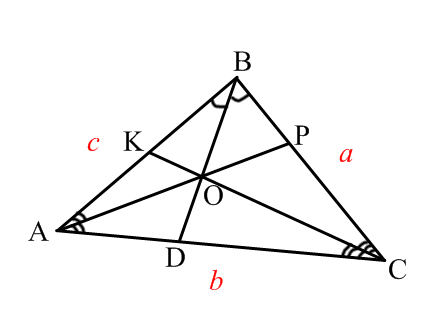 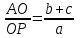 Сделайте выводы. Решить задачи: 1) Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 3:2, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 12 см. 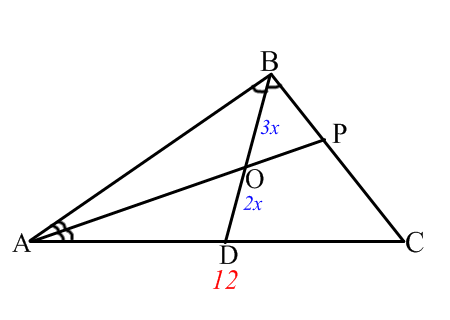 2) Биссектрисы BD и CE ∆ABC пересекаются в точке О. АВ=14, ВС=6, АС=10. Найдите ОD. 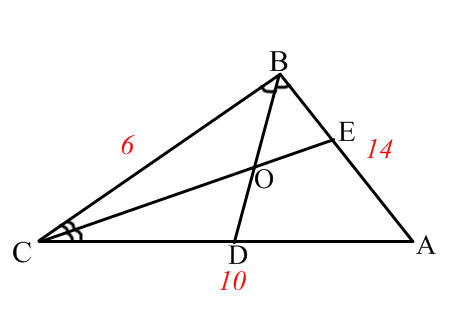 Проверить решение задач по образцу:   | -выполняет построение треугольников по условию свойств -составляет соотношение длин соответствующих сторон -поясняет все свойства -делает вывод -решают задачи -проверяют решение по образцу | ФО: Словесная оценка учителя Взаимооценивание Стратегия «Стикер» | Приложения 1-2 Презентация Слайды 4-11 Учебник 9 класс |
| Закрепление полученных знаний | Работа в группе Обсуждение в четверках: учащиеся разбираются в сложных вопросах с теми, кто сидит рядом в соседнем ряду, или с теми, кто сидит на следующей парте.
Пояснить. | -выполняет построение треугольников по условию задачи -решают задачи -поясняют ответ -делают вывод. | ФО: взаимное оценивание по критериям, самопроверка по образцу, комментарии учителя | Приложение 2 Презентация Слайды 12-13 Учебник 9 класс |
| Активизация опорных знаний | Работа у доски. Дифференциация по уровням сложности:  | -выполняют построение треугольников по условию задачи -проверяют правильность решения задач -поясняют ответ -делают выводы. | ФО: взаимное оценивание по критериям, самопроверка по образцу, комментарии учителя | Презентация Слайд 14 Учебник 9 класс |
| Домашнее задание | Домашнее задание. Знать определения, решить из уровня А-В учебного пособия. | Записывают дз в тетрадь | | |
| Рефлексия | Подведем итоги. Чем мы занимались на уроке? Какие были цели урока? Выполнили мы их? Рефлексия –Оцените свою работу на уроке -И завершить урок хотела бы словами Лобочевского: «Только с геометрией начинается строгое математическое учение.» (Н.И. Лобачевский) | Учащиеся подытоживают свои знания по изучаемой теме. | ФО: Стратегия «Стикер» | Слайды 15-16 |
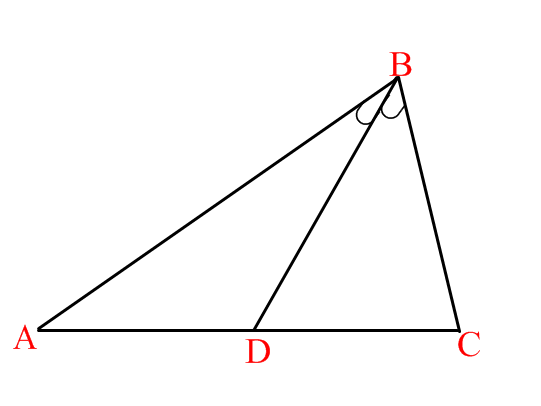
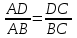 войство биссектрисы: В треугольнике биссектриса делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.
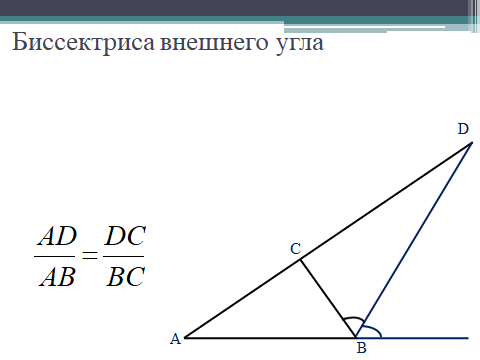
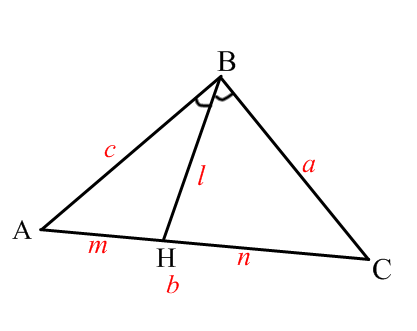
войство биссектрисы: В треугольнике биссектриса делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.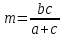 ормула нахождения длин отрезков, на которые биссектриса делит противоположную сторону треугольника
ормула нахождения длин отрезков, на которые биссектриса делит противоположную сторону треугольника