Файл: Разработка урока тренинга по теме Подготовка к огэ. Площадь треугольника.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 8
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Муниципальное автономное общеобразовательное учреждение
средняя общеобразовательная школа № 45
Разработка урока- тренинга по теме
«Подготовка к ОГЭ. Площадь треугольника»,
геометрия, 9 класс.
Автор: учитель математики
первой категории
МАОУ СОШ №45 г. Калининграда
Борисова Алла Николаевна.
г. Калининград
2017 – 2018 учебный год
Автор – Борисова Алла Николаевна
Образовательное учреждение – муниципальное автономное общеобразовательное учреждение средняя общеобразовательная школа № 45 города Калининграда
Предмет – математика (геометрия)
Класс – 9
Тема – «Подготовка к ОГЭ. Площадь треугольника»
Учебно-методическое обеспечение:
-
Геометрия, 7 - 9: учебник для общеобразовательных учреждений/ Л. С. Атанасян и др., - 17 - е изд., - М.: «Просвещение», 2016 г. -
ОГЭ 2018. Математика. 50 вариантов. Типовые тестовые задания/И. Р. Высоцкий - М.: «Экзамен», 2018 г. -
Я сдам ОГЭ! Модульный курс. Математика. Практикум и диагностика./ И. В. Ященко, С. А. Шестаков, - М.: «Просвещение», 2017 г.
Данные о программах, в которых выполнена мультимедийная составляющая работы - Microsoft Office Power Point 2010
Цель: повторить знания по теории геометрии, продолжить работу по решению геометрических задач по теме «Площадь треугольника» для подготовки к ОГЭ.
Задачи урока:
Образовательные:
-
систематизировать знания учащихся по ключевым разделам планиметрии; -
создать содержательные и организационные условия для применения школьниками комплекса знаний для решения задач, включаемых в материалы ОГЭ.
Развивающие:
-
развивать личностно-смысловые отношения учащихся к изучаемому предмету; -
способствовать формированию коллективной и самостоятельной работы; -
формировать умение четко и ясно излагать свои мысли; -
развитие внимания, мышления, наблюдательности, активности; -
развитие умений применять полученные знания на практике.
Воспитательные:
-
воспитывать дисциплинированность, высокую работоспособность и организованность; -
воспитание познавательной активности, культуры общения, ответственности; -
привить учащимся навыков самостоятельной работы; -
воспитывать умение проводить оценку и самооценку знаний и умений.
Оборудование и материалы для урока: проектор, экран, презентация для сопровождения урока.
Тип урока: урок - тренинг.
Структура урока:
| № n/n | Название этапа урока | Время |
| 1 | Организационный момент. | 1 мин |
| 2 | Проверка теоретических знаний. | 10 мин |
| 3 | Решение задач по готовым чертежам. | 14 мин |
| 4 | Самостоятельное решение задач. | 18 мин |
| 5 | Подведение итогов урока. | 2 мин |
Ход урока.
I. Организационный момент.
Учащимся сообщается тема урока и цели, подчеркивается актуальность данной темы при сдаче ОГЭ (слайд №1).
II. Актуализация знаний учащихся
1) Проверка теоретических знаний (слайды № 2 - 4).
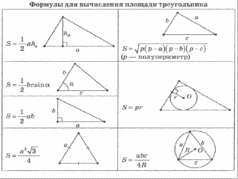

2) Учащиеся выполняют теоретический тест по выбору верных утверждений (прототип задания № 20 ОГЭ) (слайд №4).

III. Решение задач по готовым чертежам. Фронтально.
(слайды № 5 - 13).
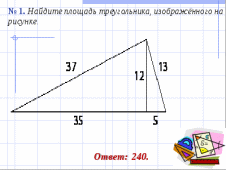
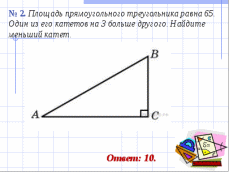



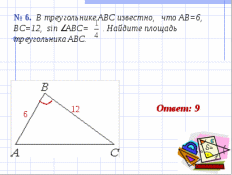
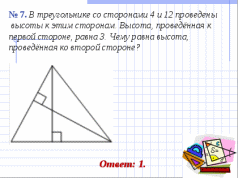
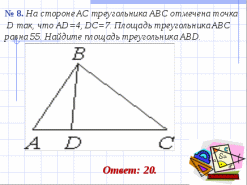
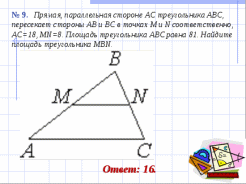
IV. Самостоятельное решение задач.
I уровень. Работают самостоятельно по карточке (по необходимости пользуются помощью учителя или соседа по парте). Двое учащихся работают на откидной доске. После окончания работы взаимопроверка.
Приложение 1.
| 1. На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь. | 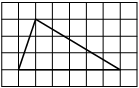 |
| 2. Найдите площадь треугольника, изображённого на рисунке. |  |
| 3. Два катета прямоугольного треугольника равны 4 и 11. Найдите площадь этого треугольника. | 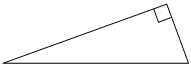 |
| 4. Площадь прямоугольного треугольника равна 99. Один из его катетов равен 33. Найдите другой катет. | |
| 5. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 24 и 25. | |
| 6. Боковая сторона равнобедренного треугольника равна 29, а основание равно 42. Найдите площадь этого треугольника. | 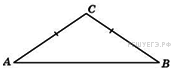 |
| 7. Найдите площадь треугольника , две стороны которого равны 4√2 и 6, а угол между ними равен 45°. | 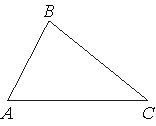 |
| 8. На стороне AC треугольника ABC отмечена точка D так, что AD=3, DC=7. Площадь треугольника ABC равна 20. Найдите площадь треугольника BCD. | 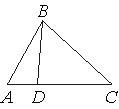 |
| 9. В треугольнике АВС известно, что AB=8, BC=10, AC=12. Найдите cos ∠ABC. | 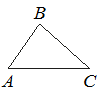 |
| 10. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=48, MN=40. Площадь треугольника ABC равна 72. Найдите площадь треугольника MBN. | 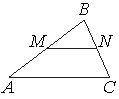 |
II уровень.
Решают задачи повышенного уровня сложности из второй части ОГЭ.
Работают в группах. При необходимости учитель даёт консультации. Затем решения оформляются на доске.
Приложение 2.
№ 1. (Задание 24). Площадь параллелограмма ABCD равна 68. Точка E — середина стороны AB. Найдите площадь треугольника CBE
№ 2. (Задание 25). Внутри параллелограмма ABCD выбрали произвольную точку Е. Докажите, что сумма площадей треугольников ВЕС и AED равна половине площади параллелограмма.
Решение.
№ 1.
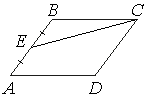
Диагональ АС делит параллелограмм на два равных треугольника АВС и ADC. Значит, SABC = SADC = ½ SABCD/
Медиана СЕ делит треугольник АВС на два треугольника СВЕ и АСЕ, равных по площади
SСВЕ = SАСЕ = ½ SABC
Значит, SСВЕ = ¼ SABCD/ = ¼ ∙68 = 17. Ответ: 17.
№ 2.
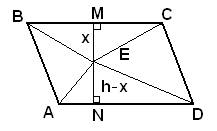
Решение.
Проведем в параллелограмме ABCD высоту MN, равную h, и проходящую через точку E. Пусть расстояние ME=x, тогда NE=h-x. Площадь параллелограмма можно вычислить как
а площади треугольников как
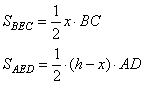
Так как в параллелограмме противоположные стороны равны, то BC=AD и сумма площадей треугольников равна
что в точности равно половине площади параллелограмма ABCD. Утверждение доказано.
V. Подведение итогов урока.
Что запомнилось на уроке?
Какие проблемы возникли?
Выставление отметок за урок.
VIII. Домашнее задание.
И. В. Ященко, С. А. Шестаков «Я сдам ОГЭ!», стр. 291, домашняя работа 114, дополнительно № 1, 2 (для II уровня учащихся)
Приложение 3.
II уровень:
1.
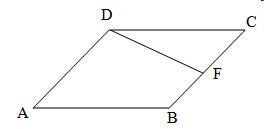
Площадь параллелограмма ABCD равна 92. Точка F - середина стороны BC. Найдите площадь трапеции ADFB.
2. На стороне CD параллелограмма ABCD отметили точку M . Найдите площадь параллелограмма, если площадь треугольника MAB равна 19.

