Файл: Полученная схема 9 постановка задачи.docx

СОДЕРЖАНИЕ



ПОСТАНОВКА ЗАДАЧИ
Синтезировать счетчик с модулем 12 и шагом 7 на T-триггерах. Определить последовательность счета, на её основе построить таблицу переходов состояний счетчика. На основе таблицы переходов сформировать таблицу управления T-триггерами. Сформировать логические функции управления

T-триггерами с учетом незадействованных состояний. Построить схему счетчика с индикацией его значений. Сделать вывод, указать информационные источники

ХОД РАБОТЫ

1 - Последовательность счета:

0 - 7 - 2 - 9 - 4 - 11 - 6 - 1 - 8 - 3 - 10 - 5 - 0

Для реализации потребуется 4 триггера:
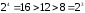
2 - Построение таблицы переходов, неиспользуемые значения заполнены знаком * (таблица 1)

Таблица 1: таблица истинности с переходами

	Q3(t)	Q2(t)	Q1(t)	Q0(t)	Q3(t+1)	Q2(t+1)	Q1(t+1)	Q0(t+1)
0	0	0	0	0	0	1	1	1	7
1	0	0	0	1	1	0	0	0	8
2	0	0	1	0	1	0	0	1	9
3	0	0	1	1	1	0	1	0	10
4	0	1	0	0	1	0	1	1	11
5	0	1	0	1	0	0	0	0	0
6	0	1	1	0	0	0	0	1	1
7	0	1	1	1	0	0	1	0	2
8	1	0	0	0	0	0	1	1	3
9	1	0	0	1	0	1	0	0	4
10	1	0	1	0	0	1	0	1	5
11	1	0	1	1	0	1	1	0	6
12	1	1	0	0	*	*	*	*	*
13	1	1	0	1	*	*	*	*	*
14	1	1	1	0	*	*	*	*	*
15	1	1	1	1	*	*	*	*	*

---

3 - Построение таблицы управления триггерами (таблица 2)
Таблица 2: таблица управления триггерами

Q3(t)	Q2(t)	Q1(t)	Q0(t)	Q3(t+1)	Q2(t+1)	Q1(t+1)	Q0(t+1)	Т3	Т2	Т1	Т0
0	0	0	0	0	1	1	1	0	1	1	1
0	0	0	1	1	0	0	0	1	0	0	1
0	0	1	0	1	0	0	1	1	0	1	1
0	0	1	1	1	0	1	0	1	0	0	1
0	1	0	0	1	0	1	1	1	1	1	1
0	1	0	1	0	0	0	0	0	1	0	1
0	1	1	0	0	0	0	1	0	1	1	1
0	1	1	1	0	0	1	0	0	1	0	1
1	0	0	0	0	0	1	1	1	0	1	1
1	0	0	1	0	1	0	0	1	1	0	1
1	0	1	0	0	1	0	1	1	1	1	1
1	0	1	1	0	1	1	0	1	1	0	1
1	1	0	0	*	*	*	*	*	*	*	*
1	1	0	1	*	*	*	*	*	*	*	*
1	1	1	0	*	*	*	*	*	*	*	*
1	1	1	1	*	*	*	*	*	*	*	*

---

4.1 - Расчет СКНФ Т3 (таблица 3). Примем неопределенные значения * за 0

Таблица 3: таблица истинности для Т3

Q3(t)	Q2(t)	Q1(t)	Q0(t)	T3
0	0	0	0	0	0
0	0	0	1	1
0	0	1	0	1
0	0	1	1	1
0	1	0	0	1
0	1	0	1	0	2
0	1	1	0	0	2
0	1	1	1	0	3
1	0	0	0	1
1	0	0	1	1
1	0	1	0	1
1	0	1	1	1
1	1	0	0	*	2*
1	1	0	1	*	3*
1	1	1	0	*	3*
1	1	1	1	*	4*

---

0	0	0	0		0
0	1	0	1
0	1	1	0
1	1	0	0	*	2
0	1	1	1
1	1	0	1	*
1	1	1	0	*	3
1	1	1	1	*	4

Производим склейки:

0	0	0	0				0	0	0	0			0	0	0	0				0	0	0	0			0	0	0	0
0	1	0	1		v		0	1	X	1			X	1	0	1		v		X	1	X	1			X	1	X	1
0	1	1	0		v		X	1	0	1			X	1	1	0		v		X	1	1	X			X	1	1	X
1	1	0	0	*	v		0	1	1	X			X	1	1	1		v		X	1	X	1			1	1	X	X
0	1	1	1		v		X	1	1	0			0	1	X	1		v		1	1	X	X
1	1	0	1	*	v		1	1	0	X	*		1	1	X	0	*	v		X	1	1	X
1	1	1	0	*	v		1	1	X	0	*		1	1	X	1	*	v		1	1	X	X
1	1	1	1	*	v		X	1	1	1			0	1	1	X		v
							1	1	X	1	*		1	1	0	X	*	v
							1	1	1	X	*		1	1	1	X	*	v

---

Наборы не участвовавшие в склейке: 0000, X1X1, X11X, 11XX

Таблица покрытия (таблица 4, темно-серым цветом отмечены неопределенные значения счетчика). Выделяем ядро в незакрашенной части

Таблица 4: таблица покрытия функции Т3

	0000	0101	0110	0111	1100*	1101*	1110*	1111*
0000	⊕
X1X1		⊕		+		+		+
X11X			⊕	+			+	+
11XX					+	+	+	+

Ядро функции - 0000, X1X1, X11X

_{Получаем:}

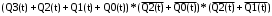
4.2 - Расчет СКНФ Т2 (таблица 5) Примем неопределенные значения * за 0

Таблица 5: таблица истинности для Т2

Q3(t)	Q2(t)	Q1(t)	Q0(t)	T2
0	0	0	0	1
0	0	0	1	0	1
0	0	1	0	0	1
0	0	1	1	0	2
0	1	0	0	1
0	1	0	1	1
0	1	1	0	1
0	1	1	1	1
1	0	0	0	0	1
1	0	0	1	1
1	0	1	0	1
1	0	1	1	1
1	1	0	0	*	2*
1	1	0	1	*	3*
1	1	1	0	*	3*
1	1	1	1	*	4*

---