ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.03.2024
Просмотров: 21
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа № 1
Линейные алгоритмы
Лабораторная работа посвящена основам составления алгоритмов и базовым понятиям языка программирования С++. Затрагиваются такие понятия как программа, переменная, тип данных, операции консольного ввода и вывода, простейшие математические операции.
Задачи
1.С горы начинают скатываться сани с ускорением 0,5 м/с2. Какой путь проходят сани, если скорость их в конце горы 36 км/ч.
2.Даны два числа. Найти среднее арифметическое их квадратов и среднее арифметическое их модулей.
3.Дана длина ребра куба. Найти площадь грани, площадь полной поверхности и объём этого куба.
4.Парашютист раскрыл свой парашют на высоте 1 км от поверхности Земли и далее двигался прямолинейно со скоростью 7 м/с по вертикали вниз. На каком расстоянии от поверхности Земли он находился через 1 минуту после раскрытия парашюта.
5.Найти длину окружности и площадь круга заданного радиуса r.
6.Найти площадь кольца, внутренний радиус которого равен r1, а внешний радиус равенr2 (r1
7.Лодка движется перпендикулярно берегу реки. Её скорость относительно воды равна 2 м/с. Определите время движения лодки к другому берегу, если ширина реки 80 м, а скорость течения 1,5 м/с.
8.Дана длина окружности. Найти площадь круга, ограниченного этой окружностью.
9.Дана сторона равностороннего треугольника. Найти площадь этого треугольника, радиусы вписанной и описанной окружностей.
10.Найти периметр и площадь равнобедренной трапеции с основаниями a иb (a >b) и угломβ при большем основании (угол задан в градусах).
11.Какую скорость приобретает после прохождения пути 200 м электропоезд, начинающий равноускоренное прямолинейное движение с ускорением 1,25 м/с2.
12.Найти расстояние между двумя точками с заданными координатами (x1,y1) и (x2,y2).
13.Найти решение системы уравнений вида:
a1x + b1y = c1,
a2x + b2y = c2
заданной своими коэффициентами a1,b1,c1,a2,b2,c2, если известно, что данная система имеет единственное решение.
14.Скорость первого автомобиля v1 км/ч, второго —v2 км/ч, расстояние между ними s км. Определить расстояние между ними через t часов, если автомобили первоначально движутся навстречу друг другу.
15.Человек переплывает реку шириной 100 м по прямой, перпендикулярной её берегам. Скорость пловца относительно берега 0,3 м/с, скорость течения 0,4 м/с. Какое расстояние преодолевает пловец относительно воды.
16.Скорость лодки в стоячей воде v км/ч, скорость течения реки u км/ч (u
17.Найти длину грани a правильного12-угольникавписанного в окружность радиусом
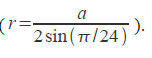
18.После удара о поверхность Земли мяч движется вертикально вверх со скоростью 15 м/с. Найдите координату мяча над поверхностью Земли через 1 секунду и через 2 секунды после начала движения.
19.Определить число сторон правильного n-угольника со стороной a, описанного вокруг окружности радиусом
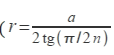
20.Определить центральный угол δ , соответствующий длине дуги l окружности радиусом r
21.Прямоугольный треугольник задан координатами вершин (x1,y1), (x2,y2), (x3,y3). Найти значение синуса острого угла.
22.Прямоугольный треугольник задан координатами вершин (x1,y1), (x2,y2), (x3,y3). Найти значение тангенса острого угла.
23.Прямоугольный треугольник задан координатами вершин (x1,y1), (x2,y2), (x3,y3). Найти значение косинуса острого угла.
24.Дана сторона a и два угла треугольника, напримерβ и γ . Найти третий угол и остальные две стороны. Использовать теорему о сумме углов треугольников и теорему синусов.
25.Даны две стороны, например a и b, и угол γ между ними. Найти остальные два угла и третью сторону. Для решения использовать теорему косинусов и/или теорему синусов.
26.Найти угол параллелограмма α , если известны его стороны a и b , а также его площадь S, если формула вычисления площади: S=a b sinα .
27.Вычислить значения функций:
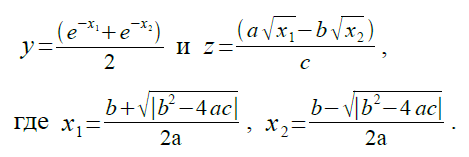
28.Вычислить площадь кругового сегмента, не равного полукругу по формуле
где r – радиус круга, α – градусная мера центрального угла (α<180°), который содержит дугу этого кругового сегмента, SΔ – площадь треугольника с вершинами в центре круга и в концах радиусов, ограничивающих соответствующий сектор.
29. Вычислить координаты точки, делящей отрезок a
1a2 в отношении n1:n2 по формулам:
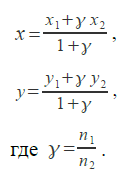
30. Вычислить координаты центра тяжести трёх материальных точек с массами m1 ,m2 ,m3 и координатами (x1 , y1), (x2 , y2), (x3 , y3) по формулам:
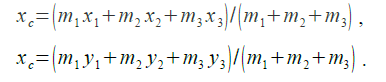
31.Вычислить медианы треугольника со сторонами a,b,c по формулам:
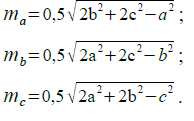
32. Вычислить значение функции y=ae−ax sinωx при x= (π /2−ϕ) /ω .
33. Вычислить площадь поверхности
и объём
усечённого конуса.34.Вычислить высоты треугольника со сторонами a,b,c по формулам:
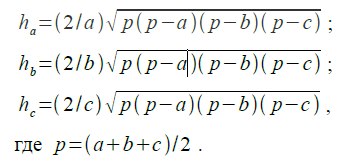
35.Определить высоту треугольника, если его площадь равна S, а основание больше высоты на величину a.
Лабораторная работа № 2
Циклы и ветвления
Лабораторная работа посвящена алгоритмам, реализующим циклы и ветвления, и операторам языка С++, позволяющим описывать такие алгоритмы. Используются циклы с предусловием, с постусловием, цикл «for», условный и тернарный операторы, оператор множественного выбора.
1. Найти U - первый отрицательный член последовательности: cos(ctg(n)) , n=1,2,3...
2. Вычислить y-первое из чисел:
меньшее по модулю 10−4 .3. Вычислить S — сумму квадратов всех целых чисел, попадающих в интервал: (ln x ,ex) при x>1 .
4. Если среди чисел sin (xn) , где n=1…30 , есть хотя бы одно отрицательное число, то переменной t присвоить это число, а иначе – значение π .
5.Дана последовательность из 100 целых чисел, созданная генератором случайных чисел. Определить, со скольких отрицательных чисел она начинается.
6.Вычислить:
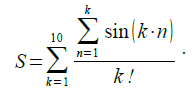
7.Вычислить:
8.Вычислить
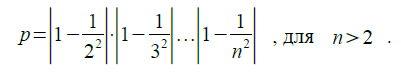
9.Определить, является ли заданное натуральное число палиндромом, т.е. таким, десятичная запись которого читается одинаково слева направо и справа налево (например: 30303, 1441).
10.Сгенерировать 100 случайных вещественных чисел. Вычислить: а) разность между максимальным и минимальным элементами; б) произведение максимального и минимального элементов.
11.Дана последовательность чисел 1…N . Вывести на печать все числа последовательности, которые являются степенью 3, 5, 7.
12. Определить, попадает ли точка с координатами x0 , y0 в круг радиусом r . Уравнение окружности r2=x2+ y2 . Вывести на экран сообщение, если точка лежит внутри круга, за его пределами или на его границе.
13.Вычислить значение:
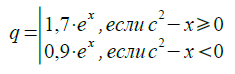
14.Определить, в каком квадранте находится точка с координатами x,y, и вывести на печать номер квадранта.
15.Вычислить корни квадратного уравнения вида
16.Вычислить значение функции:
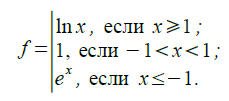
17. Вычислить и вывести на экран значения функции y = a3/ (a2 + x2 ) при x , изменяющимся от 0 до 3 с шагом 0,1.
18. Вычислить:
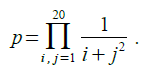
19. Вывести на экран положительные значения функции
при n=1…50.
20.Определить, является ли заданное натуральное число совершенным, т.е. равным сумме всех своих (положительных) делителей, кроме самого этого числа (например, число 6 совершенно: 6 = 1 + 2 + 3).
21.Найти наименьшее значение функции
в интервале изменения аргументаx от 0 до c с шагом h .22.Вычислить сумму четных и сумму нечетных чисел натурального ряда от 1 до n.
23.Вычислить сумму положительных и сумму отрицательных значений функции,
24. Для функции z=xk /k2 определить k , при котором z становится меньше a .
25.Вычислить:
.26.Определить число, получаемое выписыванием в обратном порядке цифр заданного натурального числа.
27.Найти экстремальное значение функции
при изменении аргументаx от 0 до 4 с шагом h . Функция такого вида имеет один экстремум. Если c>0 , то следует искать минимум, если c<0 , то минимум.28. Рассчитать траекторию движения снаряда по формулам
при постоянных скоростях Vx , Vy. Время t изменяется от нуля с шагом Δt.29.Вычислить значение функции z=x3/y , где y=sin(nx)+ 0,5 .
30.Вокруг равностороннего треугольника со стороной А описана окружность. Вычислить количество сторон описанного многоугольника, при котором его периметр отличается от периметра описанной окружности не более чем на величину ε.
31.Найти сумму цифр заданного натурального числа.
32. Определить с точностью 0,2 точку пересечения функции
с осью x при изменении аргумента x от b0 до bm с шагом 0,2. Сначала следует определить знак функции y при x=b0 . Изменение знака функции является признаком пересечения оси x.33.Определить и вывести на экран трёхзначные натуральные числа, сумма цифр которых равна n (1≤n≤27).
34.Даны координаты (как целые числа от 1 до 8) двух различных полей шахматной доски. Определить, может ли конь за один ход перейти с одного поля на другое.
35.Найти среднее арифметическое и среднее геометрическое действительных положительных корней 100 квадратных уравнений вида:
Лабораторная работа № 3
Одномерные массивы и строки
Лабораторная работа посвящена векторным типам данных, понятию одномерных массивов и строк. Рассматриваются такие понятия как линейная память, адресация, указатель, операции разыменования указателя и получения адреса, ASCII-код, терминальный нуль.