Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)


Кафедра радиоэлектроники и систем связи (РСС)


ОТЧЁТ

по Лабораторной работе №1

«Экспериментальная проверка токораспределения в разветвленных цепях постоянного тока»
По дисциплине «Основы теории цепей»


Выполнил:

Студент гр.

Томск 2022 г.

Введение

Цель работы является измерения и приобретение навыков сборки испытания электрических цепей на экране персонального компьютера с помощью пакета ASIMEC. Теоретические расчеты и их экспериментальное подтверждение.

Выполнение работы

Согласно варианту, даны величины напряжения и сопротивления:

Е₁=21В; Е₂ =16В; Е₃ =12В; R₁ = 60 Ом; R₂ = 30 Ом; R₃ = 43 Ом; R₄= 68 Ом; R₅ = 20 Ом;
Для проведения эксперимента использовалась схема, приведенная на рисунке 1.



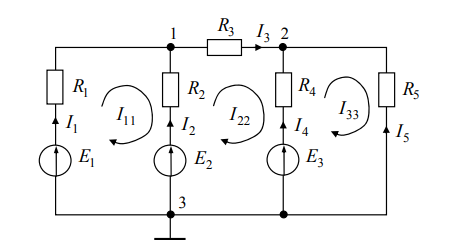
Рисунок 1

1. 
   Рассчитать токи всех ветвей цепи методом контурных токов.
   

I₁₁(R₁+R₂)-I₂₂R₂=E₁-E₂

-I₁₁R₂+I₂₂(R₂+R₃+R₄) –I₃₃R₄=E₂-E₃

-I₂₂R₄+I₃₃ (R₄+R₅)=E₃

I₁₁=0,119029 А; I₂₂=0,190421 А; I₃₃=0,283507 А.

2. 
   Определить токи всех ветвей экспериментально.
   

Таблица 1.

Условия получения значения параметра	Параметры
	I1, мА	I2, мА	I3, мА	I4, мА	I5, мА
Расчет	119	71,4	190,4	93,1	283,5
Эксперимент	119	71,39	190,4	93,09	283,5

I₁= I₁₁=119 мА;

I₂= I₂₂- I₁₁=190,4-119=71,4 мА;

I₃= I₂₂=190,4 мА;

I₄= I₃₃- I₂₂=283,5-190,4=93,1 мА;

I₅

---

= I₃₃=283,5 мА;



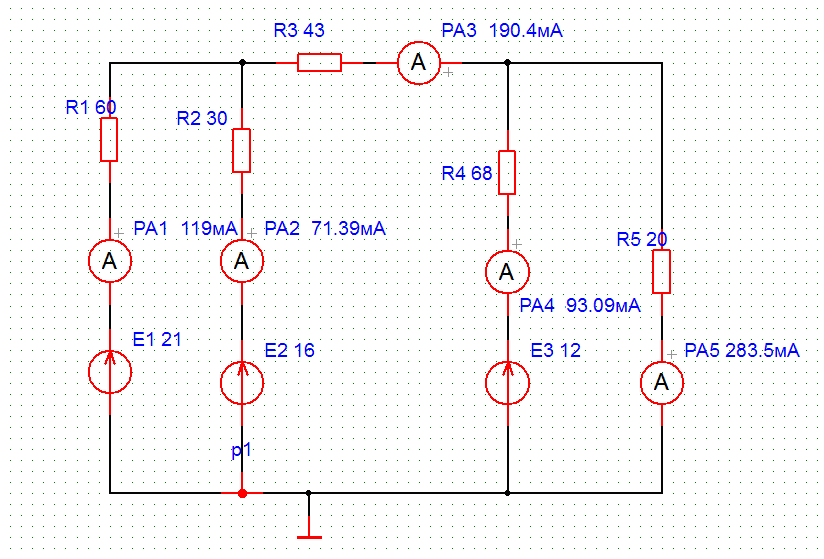
Рисунок 2.
Рисунок 2.

3. 
   Проверить экспериментально метод наложения.
   

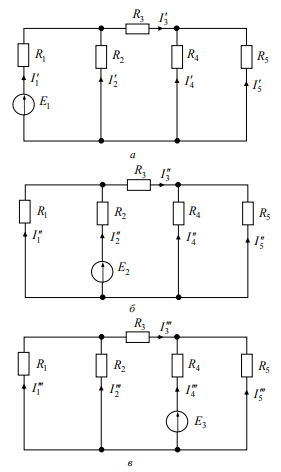
Рисунок 3


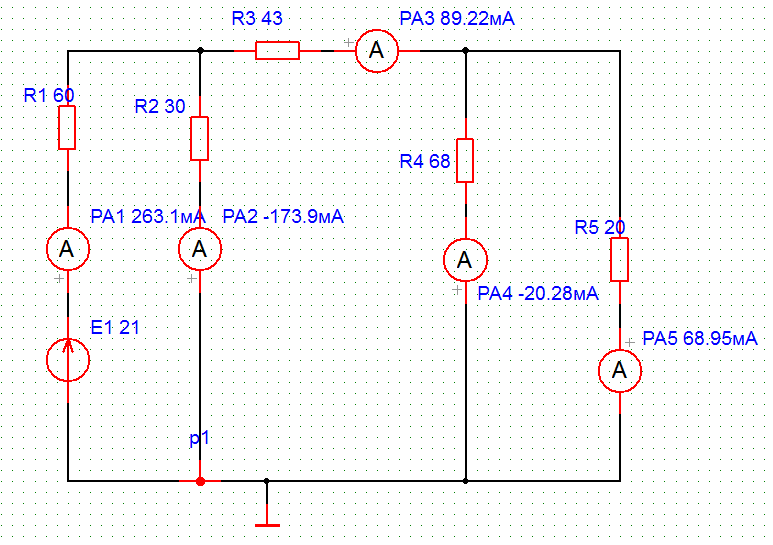
а



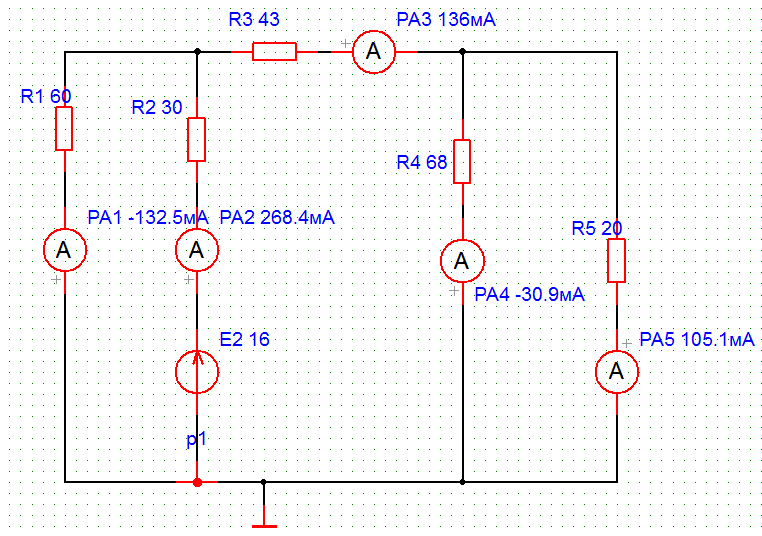
б



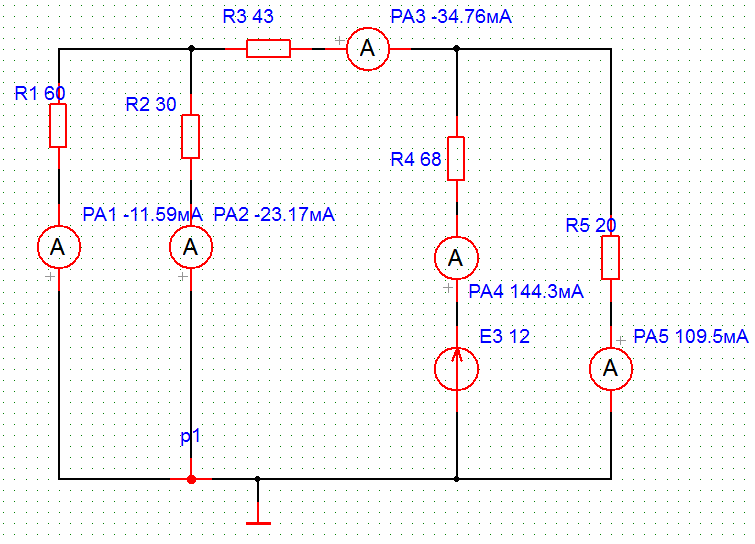
в

Рисунок 4.

Таблица 2.

Частичная схема	Токи ветвей
	I1, мА	I2, мА	I3, мА	I4, мА	I5, мА
Рис. 3а	263,1	-173,9	-20,28	93,1	68,95
Рис. 3б	-132,5	268,4	-30,9	93,09	105,1
Рис. 3в	-11,59	-23,17	144,3	93,09	109,5
Полные точки	119,01	71,33	93,12	93,09	283,55
Расчетные точки	119	71,4	93,1	93,09	283,5

4. 
   Проверить экспериментально выполнение второго закона Кирхгофа.
   

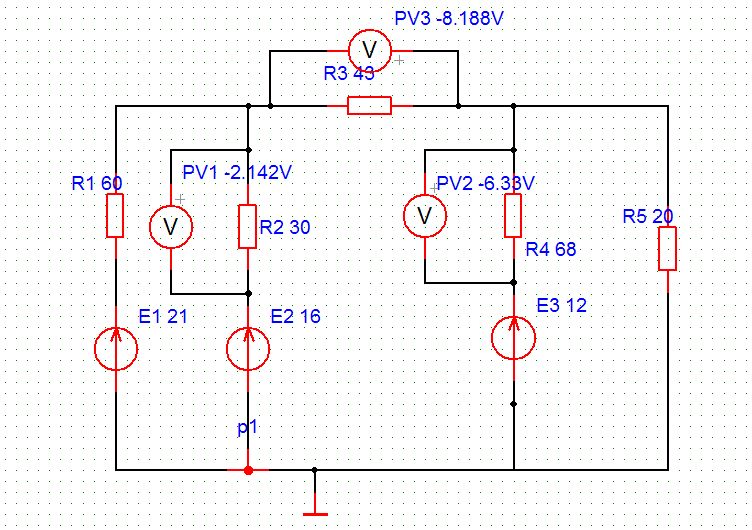
Рисунок 5.

Таблица 3.

Е2	Е3	Алгебраическая сумма ЭДС	ER2	ER3	ER4	Алгебраическая сумма напряжений
16	12	4	2,142	8,188	6,33	4

Алгебраическая сумма напряжений:

ER₂+ ER₃

---

- ER₄=2,142+8,188-6,33=4В

Алгебраическая сумма ЭДС:

Е₂- Е₃=16-12=4

5. 
   Рассчитать потенциалы узлов.
   

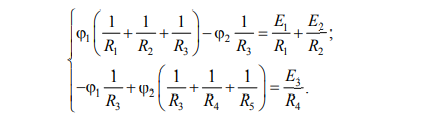
₁=35879/2589=13,858

₂=14680/2589=5,67

6. 
   Определить потенциалы узлов экспериментально.
   

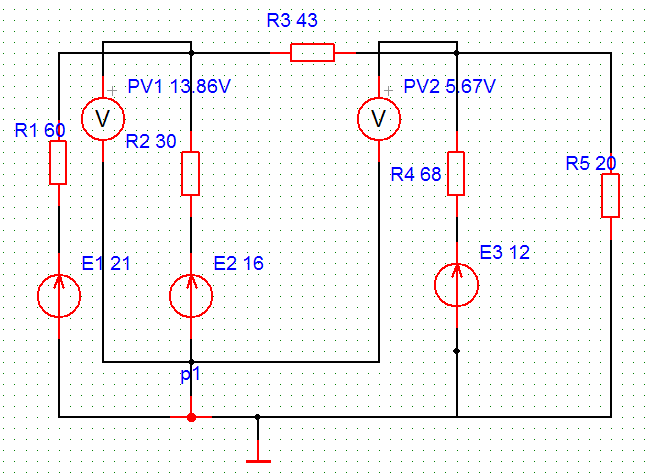
Рисунок 6.

7. 
   Проверить возможность замены треугольника сопротивлений эквивалентной звездой.
   

Согласно варианту, даны величины напряжения и сопротивления:

Е=27В; R₁ = 90 Ом; R₂ = 180 Ом; R₃ = 220 Ом; R₄= 240 Ом; R₅ = 90 Ом;

R₆= 70 Ом;

Исходная схема цепи с треугольником сопротивлений R2, R3, R4 относительно узлов а, b, с приведена на рис. 7



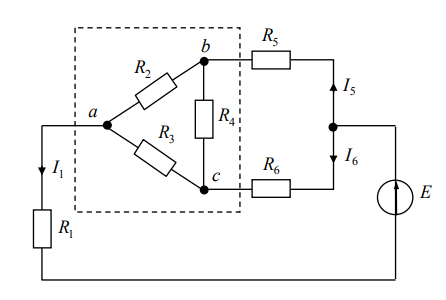
Рисунок 7.

Схема по рис. 6, включив последовательно с резисторами R1, R5, R6 амперметры показана на рис.8



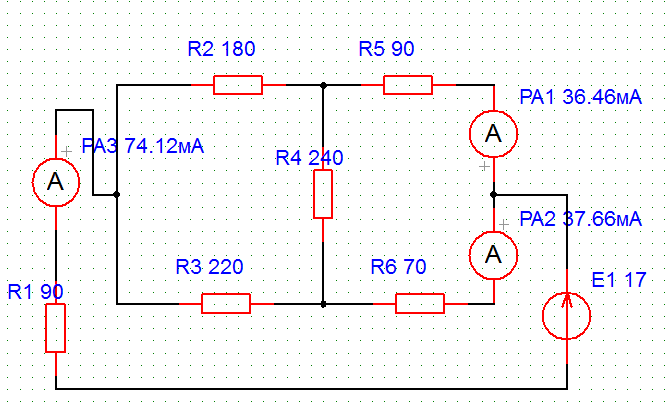
Рисунок 8.
Схема цепи с эквивалентной звездой представлена на рис.9 Параметры элементов эквивалентной звезды рассчитываются по формулам:
R₇= R₂ R₃/ R₂+ R₃+ R₄ =180∙220/180+220+240=39600/640+61,875;
R₈= R₂ R₄/ R₂+ R₃+ R₄ =180∙240/180+220+240=43200/640+67,5;
R₉= R₃ R₄/ R₂+ R₃+ R₄ =220∙240/180+220+240=52800/640+82,5.


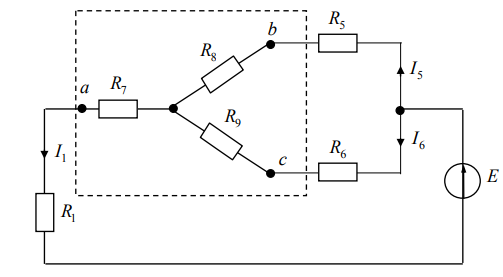
Рисунок 9.

Рассчитать сопротивления эквивалентной звезды R7, R8, R9, включить их вместо резисторов R2, R3, R4 относительно точек а, b, с. В получившейся схеме (см. рис. 9) замерить токи I1, I5, I6.



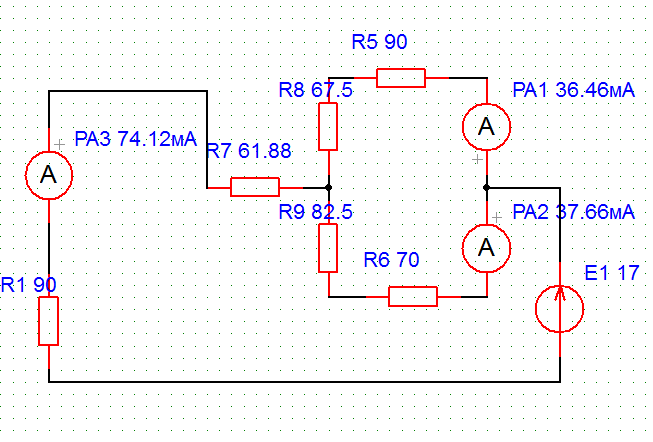
Рисунок 10.

Таблица 4.

Схема	Токи
	I1 А	I5 А	I6 А
Рис. 8 (исходная с треугольником)	0,074	0,036	0,038
рис. 10 (эквивалентная со звездой)	0,074	0,036	0,038

8 Проверить возможность замены звезды сопротивлений эквивалентным треугольником. Исходная схема цепи со звездой сопротивлений R7, R8, R9 приведена на рис. 9.

---

Параметры элементов: Е=20В; R₁ = 80 Ом; R₅ = 130 Ом; R₆ = 100 Ом;

R₇= 300 Ом; R₈ = 220 Ом; R₉= 140 Ом;

Собрать схему по рис. 9, включив последовательно с резисторами R1, R5, R6 амперметры, и замерить токи I1, I5, I6 (см. рис. 11)



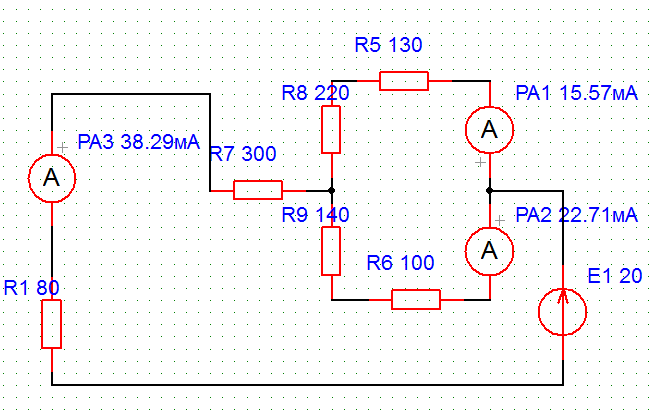
Рисунок 11.

Схема цепи с эквивалентным треугольником представлена на рис. 7. Параметры элементов эквивалентного треугольника рассчитываются по формулам:

R₂= R₇+R₈+ (R₇ R₈/ R₉) =300+220+(300∙220/140)=991,4286;
R₃= R₇+R₈+ (R₇ R₉/ R₈) =300+220+(300∙140/220)=710,909;

R₄= R₈+R₉+ (R₈ R₉/ R₇) =220+140+(220∙140/300)=462,667.
Рассчитать сопротивления эквивалентного треугольника R2, R3, R4, включить их вместо резисторов R7, R8, R9 относительно точек а, b, с. В получившейся схеме (см. рис. 12) замерить токи I1, I5, I6.


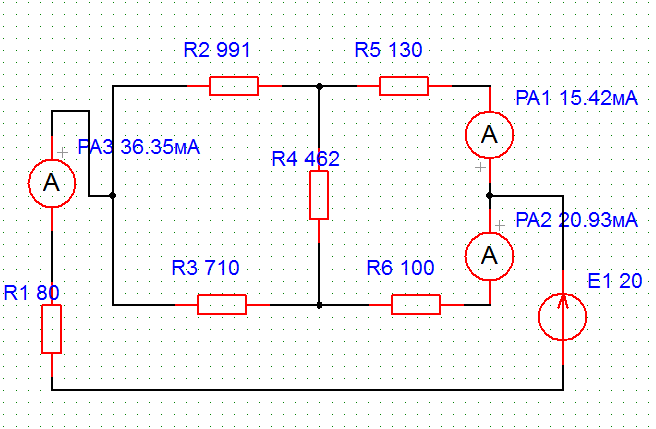
Рисунок 12
Таблица 5.

Схема	Токи
	I1 А	I5 А	I6 А
Рис. 11 (эквивалентная со звездой)	0,038	0,016	0,023
рис. 12(исходная с треугольником)	0,036	0,015	0,021

Вывод: Рассчитал и экспериментально проверил:

Метод контурных токов, в каждом независимом контуре течет свой контурный ток.

Метод наложения, ток в любой ветви электрической цепи равен алгебраической сумме частотных токов этой ветви.

Второй закон Кирхгофа, алгебраическая сумма ЭДС замкнутого контура равна алгебраической сумме падений напряжений в нем.

Метод узловых потенциалов равен алгебраической сумме токов, полученных от деления ЭДС ветвей, подходящих к узлу, на сопротивления данных ветвей (со знаком «плюс» токи тех ветвей, ЭДС которых направлены к узлу и со знаком «–» — ЭДС которых направлены от узла).

При замене треугольника сопротивлений эквивалентной звездой потенциалы одноименных точек и подтекающие к ним токи не изменяются и во внешней цепи также не произойдет никаких изменений. 

---

Иными словами, эквивалентные Δ и Y цепи ведут себя одинаково.

---

Смотрите также файлы

• Структура рабочей программы по учебному предмету, курсу в соответствии с фгос в соответствии с требованиями фгос ооо.docx

• Алгоритмизация вычислительных процессов Алгоритмизация.doc

• Agileманифест.docx

• Программам В истории Нижнего, В сердце каждого.docx

• С. Ю. Сало индивидуальная физическая подготовка военнослужащих и сотрудников войск национальной гвардии по методике федерации тактикоциклической стрельбы методическое пособие.pdf