,Карагандинский Технический Университет имени Абылкаса Сагинова
Кафедра: Энергетические

системы


Расчетно-графическая работа №1


Дисциплина: Теоретические основы электротехники

Выполнил: студентки группы

ЭЭ – 21 - 4

Сорокиной Ю.В.

Проверил: ст. преподаватель

Биличенко Е.Н.

Караганда 2022

Расчетно-графическая работа №1

Тема: Электрические цепи постоянного тока

Таблица 1 – Исходные данные

Вариант	R1	R2	R3	R4	R5	R6	E1	E2	E3		J1	J2	J3		φ=0
	Ом						В			А
39	2	4	5	2	8	14	7	-	15		0,2	-	-		с

Задание 1. Составить на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы.



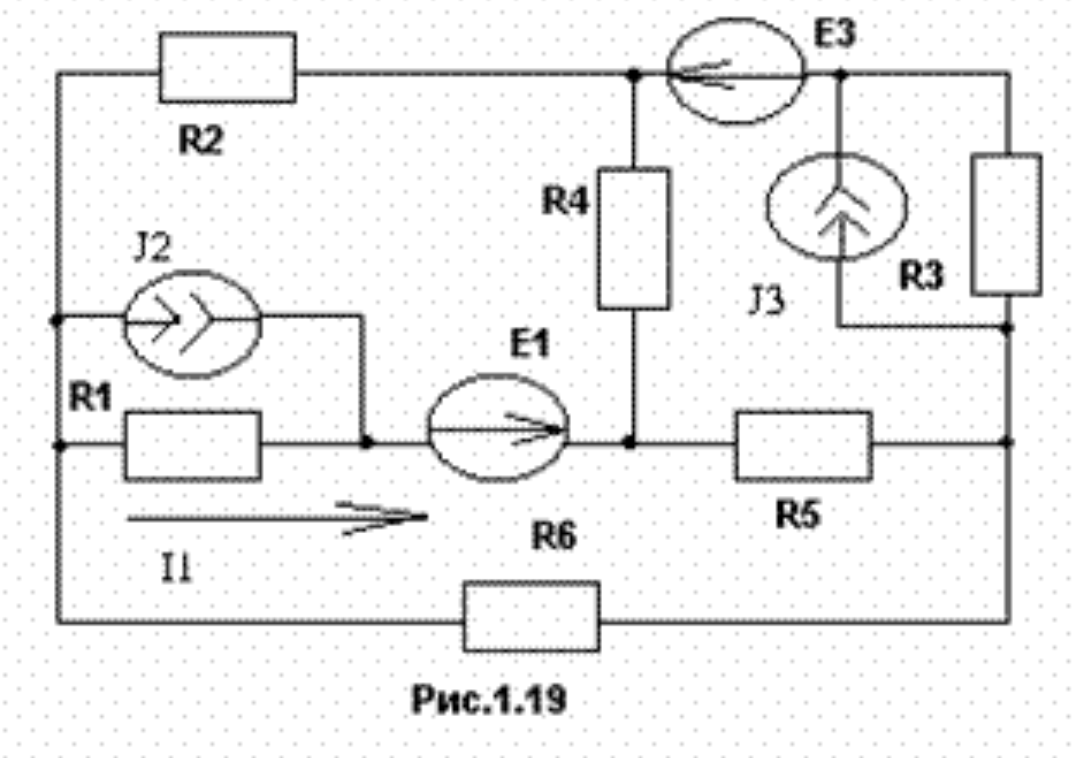
Рисунок 1. Исходная схема

Для упрощения выполнения задания преобразуем источник тока в источник ЭДС, для этого воспользуемся формулой:



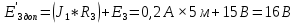
Так как в исходных данных J₂ и J₃ отсутствуют, то мы в условиях упрощения можем исключить данные элементы их схемы (рисунок 2)



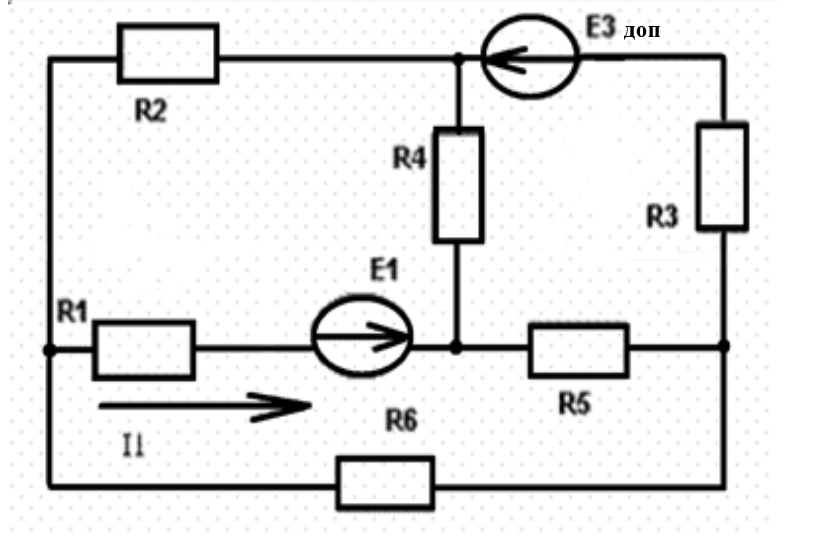
Рисунок 2. Преобразованный источник ЭДС E’₃

Произвольно расставляем направления токов в ветвях. За направление обхода контура возьмем ход по часовой стрелке (рисунок 3).

---

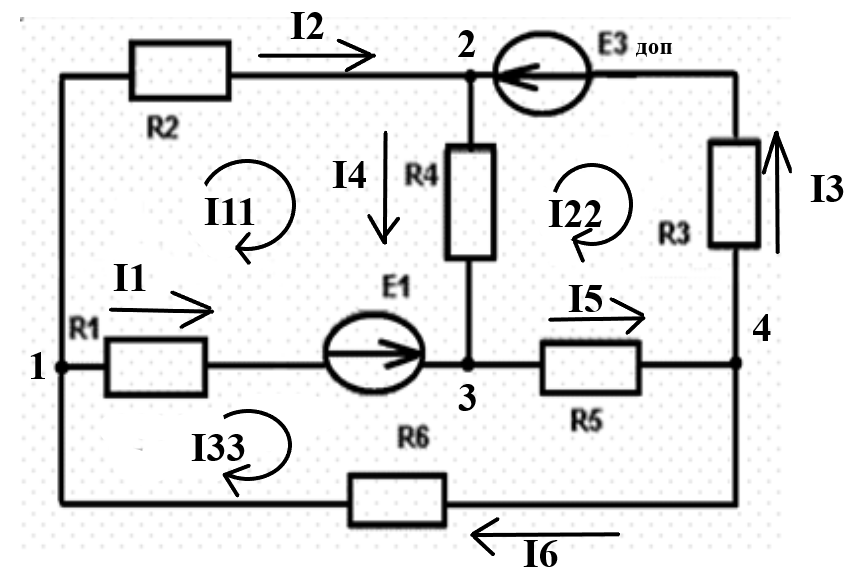
Рисунок 3. Расставленные направления токов и обходы контуров
На основании законов Кирхгофа составляем систему уравнений для расчета токов во всех ветвях схемы.
По первому закону Кирхгофа:


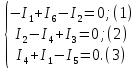
По второму закону Кирхгофу:


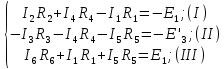
Задание 2. Определить токи во всех ветвях схемы методом контурных токов.

Составляем систему уравнений по методу контурных токов:


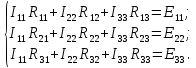
Где 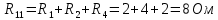. (R₁₁ - сумма сопротивлений в первом контуре);

;

;

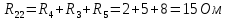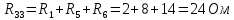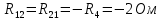(R₁₂ - сопротивление между первым и вторым контурами);

;

;

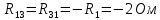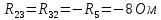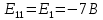(E₁₁ - сумма ЭДС в первом контуре);

;

.
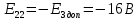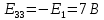Подставляем значения сопротивлений и ЭДС и получаем систему уравнений (взаимные сопротивления возьмем со знаком «-»):


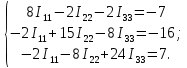
Решим систему уравнений методом Крамера. Определители:

;

;

;


;
;
.
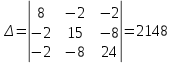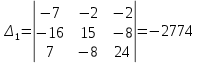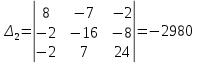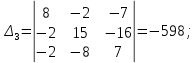
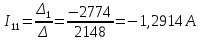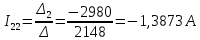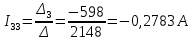Зная контурные токи, найдем токи в ветвях:

---

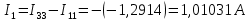
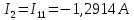
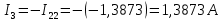
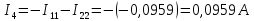
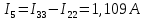
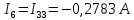
Метод контурных токов проверяется по второму закону Кирхгофа:


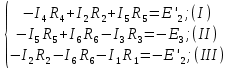
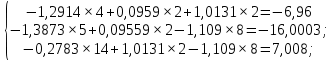
Задание 3. Определить токи во всех ветвях схемы методом узловых потенциалов.

Для расчёта цепи методом узловых потенциалов заземляем четвертый узел (рисунок 4).



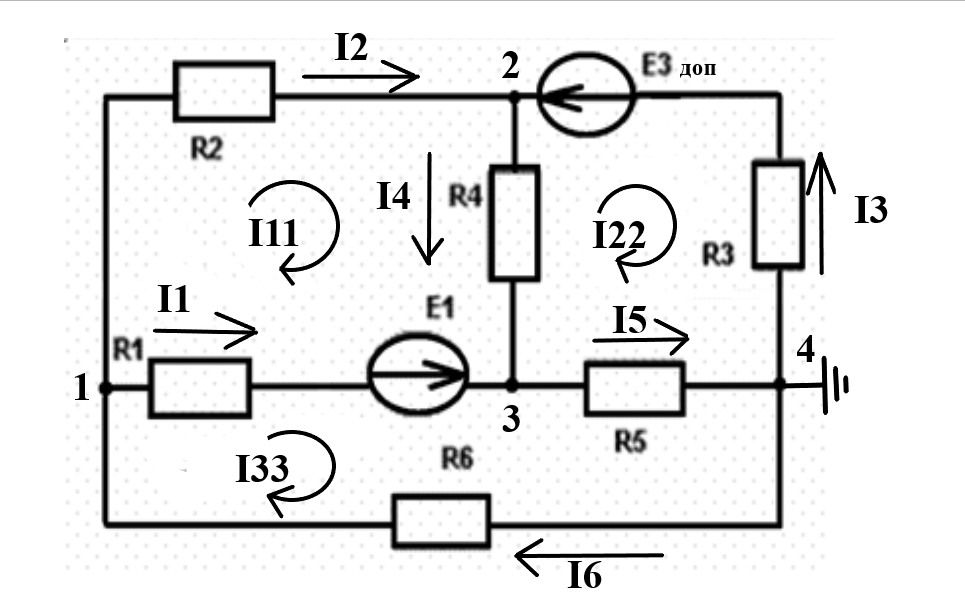
Рисунок 4. Схема с заземлённым 4-ым узлом
Составляем систему уравнений по методу узловых потенциалов:


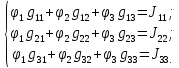
Где 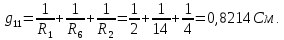(g₁₁ - сумма проводимостей ветвей, присоединенных к узлу 1);

;

;

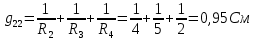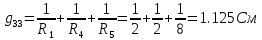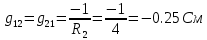. (проводимость между первым и вторым узлами);

;

;

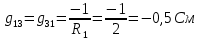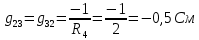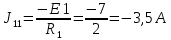. (J₁₁ – расчётный ток, определяемый как алгебраическая сумма произведений ЭДС источника на проводимость соответствующей ветви, которая присоединена к первому узлу);

;



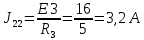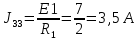
Подставляем значения проводимостей и расчётных токов и получаем систему уравнений:


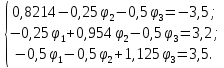
Решаем систему уравнений методом Крамера. Определители:

;
;
;

---

;
;
.
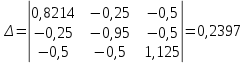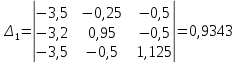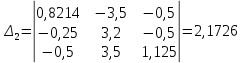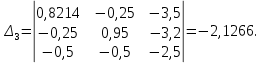
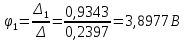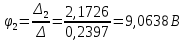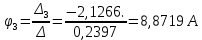Зная узловые потенциалы, найдем токи в ветвях:

;

;

;

;

;

.
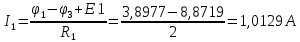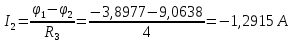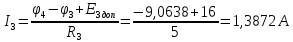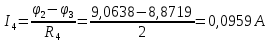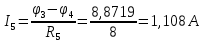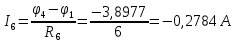Проверка метода узловых потенциалов проверяется по первому закону Кирхгофа:



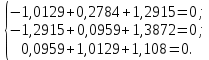
Задание 4. Результаты расчёта токов, проведенного двумя методами, свести в таблицу и сравнить между собой.
Таблица 2. Сравнение результатов расчёта токов, проведенного двумя методами

	I1, А	I2, А	I3, А	I4, А	I5, А	I6, А
Метод контурных токов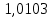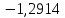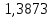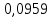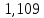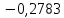
Метод узловых потенциалов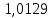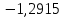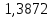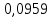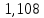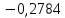

---

Задание 5. Для схемы с источником тока составить баланс мощностей, вычислив суммарную мощность источников и суммарную мощность нагрузок.

Для нахождения баланса мощностей воспользуемся следующей формулой:



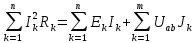
Поскольку в нашей схеме отсутствуют источники тока, то формула приобретёт вид:








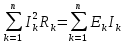
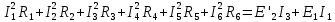
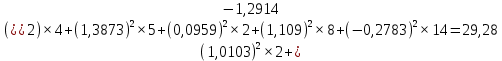
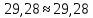
Задание 6. Определить ток I₁ в заданной схеме методом эквивалентного генератора.

Для расчёта цепи методом эквивалентного генератора вынесем из схемы ветвь с током I₁ (рисунок 5).



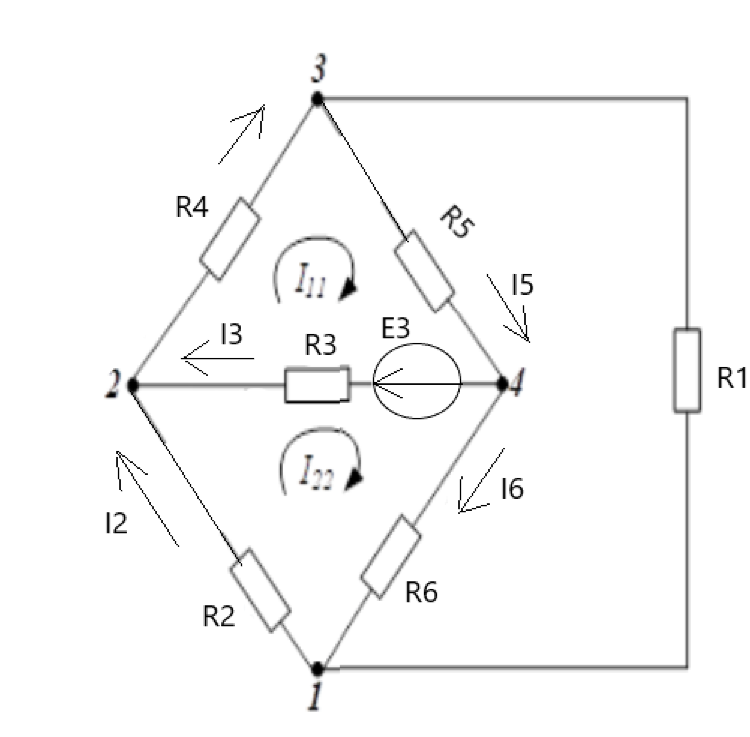
Рисунок 5. Преобразованная схема
Для нахождения токов I₂ и I₆ составляем уравнения для метода контурных токов:

→
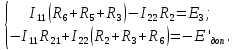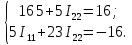
Решаем систему методом Крамера. Определители:

;

;

.
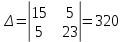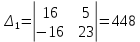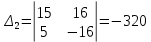Зная контурные токи, определяем токи I₃ и I₆:

;

;
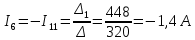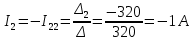Определяем напряжение холостого хода между узлами 1 и 3:

U_13хх=I₂R₂+I₄R₄= 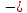1*2+1,4*4= 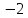+5,6=3,6В.

Далее рассчитываем входное сопротивление цепи (сопротивления первого контура преобразовываем в звезду – рисунок 6):


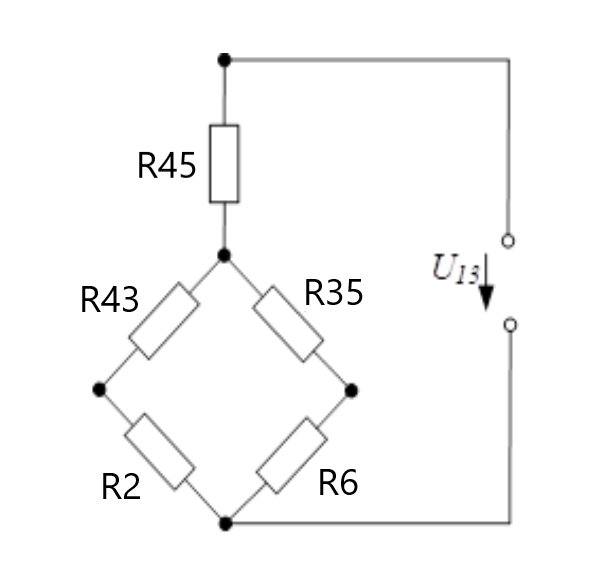
Рисунок 6 - Треугольник, преобразованный в звезду

---

Смотрите также файлы

• Профессиональный стандарт педагога как инструмент повышения качества образования.docx

• Таырып Геоэкономиканы зерттеу пні мен зектілігі. Шаруашылыты йымдастыруды ауматы факторлары. Дниежзі елдеріні экономикалы даму крсеткіштері азастан Республикасы экономикалы дамуындаы масатты крсеткіштер мен индикаторлар. Оу масаты.docx

• Все цепи питания.docx

• Решение задач по предмету История государства и права зарубежных стран.docx

• 1. Правовой статус предпринимателя Предприниматель.docx