ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.03.2024
Просмотров: 14
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ
КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра «Теория электрических цепей»
Лабораторная работа №33
Исследование активных интегрирующих и дифференцирующих цепей
по дисциплине
«Теоретические основы электротехники»
Выполнил:
Студент гр. БИН2106 Погодин Д.С.
Проверил:
Микиртичан А. Г.
Москва
2022
Цель работы:
С помощью машинного эксперимента получить форму напряжения на выходе активных интегрирующих и дифференцирующих цепей при различных формах напряжения на входе. Сравнить полученные характеристики с помощью программы Micro-Cap, с аналогичными характеристиками, полученными расчетным путем.
Предварительный расчет:
Нарисовать кривые напряжения на входе и выходе интегрирующей цепи, показанной на рис. 1, если входное напряжение имеет синусоидальную форму, прямоугольную и треугольную форму соответственно. Принять K1=10.
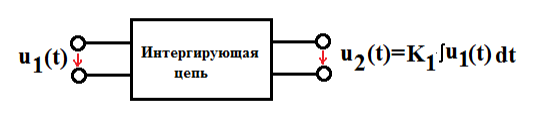
Рис. 1
Рассчитать комплексную передаточную функцию H для активной цепи (рис. 2). Нарисовать кривые напряжения на входе и выходе активной интегрирующей цепи, показанной на рис. 2, если входное напряжение имеет синусоидальную форму, С=244 нФ, R=2440 Ом. 94
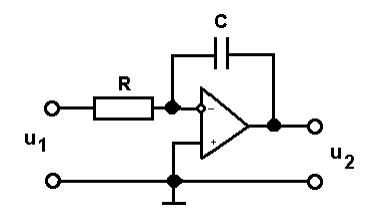
Рис. 2
Нарисовать кривые напряжения на входе и выходе дифференцирующей цепи, показанной на рис. 3, если входное напряжение имеет синусоидальную форму, прямоугольную и треугольную форму соответственно. Принять K2=6.

Рис. 3
Рассчитать комплексную передаточную функцию H для активной цепи (рис. 4). Нарисовать кривые напряжения на входе и выходе дифференцирующей цепи, показанной на рис. 4, если входное напряжение имеет синусоидальную форму, С=244 нФ, R=2440 Ом.
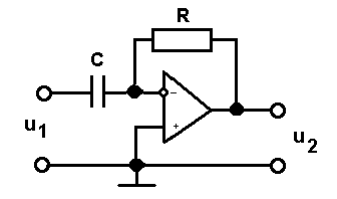
Рис. 4
Порядок выполнения работы:
Входное напряжение
Для всех схем принять
( ) sin(2 ), 1 u t U ft
m - синусоидальное входное напряжение
где Um=1 В – амплитуда входного напряжения;
f=2 кГц – частота входного напряжения;
t[0; 1] мс – время.
u1(t) - прямоугольное входное напряжение (рис. 31)
VZERO=–1 – минимальное значение, В;
VONE=1 – максимальное значение, В;
Р1=0 – начало переднего фронта, с;
Р2=0 –начало плоской вершины импульса, с;
Р3=0.25e-3 – конец плоской вершины импульса, с;
Р4=0.25e-3 – момент достижения уровня VZERO, с;
P5=0.5e-3 – период следования импульсов, с.
u1(t) - треугольное входное напряжение (рис. 35);
VZERO=-1, VONE=1, P1=0, P2=0.25e-3, P3=0.25e-3, P4=0.5e-3, P5=0.5e-3.
Для интегрирующей цепи
где
u2(t) – выходное напряжение;
K1 – коэффициент пропорциональности.
Для активной интегрирующей цепи
Для дифференцирующей цепи
где
u2(t) – выходное напряжение;
K2 – коэффициент пропорциональности.
Для активной дифференцирующей цепи
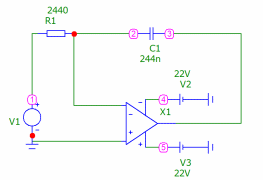
Рис. 5 – цепь 1 (схема с источником синусоидального напряжения резистором и конденсатором)
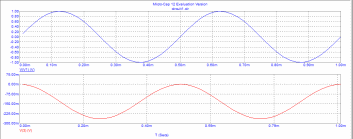
Рис.6 - зависимости напряжений на входе u1(t)=V(V1) и выходе u2(t)=V(3) интегрирующей цепи от времени t
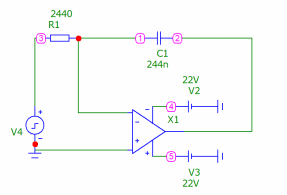
Рис.7 – цепь 2(схема с импульсным источником резистором и конденсатором)
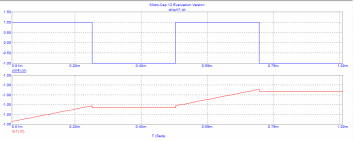
Рис. 8 - зависимости напряжений на входе u1(t)=V(V4) и выходе u2(t)=V(1) интегрирующей цепи от времени t при воздействии прямоугольными импульсами.
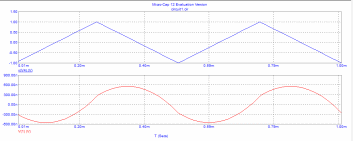
Рис. 9 - зависимости напряжения на выходе операционного усилителя и импульсного источника
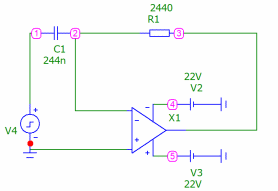
Рис. 10 - дифференцирующую цепь (рис. 4) с входным импульсным
источником
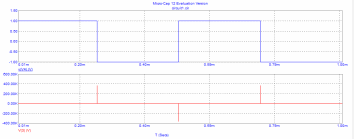
Рис. 11 - зависимости напряжений на входе u1(t)=V(V4) и выходе u2(t)=V(3)
дифференцирующей цепи от времени t.
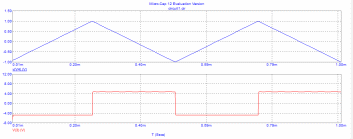
Рис. 14 - зависимости напряжений на входе u1(t)=V(V4) и выходе u2(t)=V(3) дифференцирующей цепи от времени t.
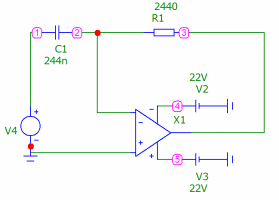
Рис. 12 - дифференцирующую цепь (рис. 4) с входным синусоидальным
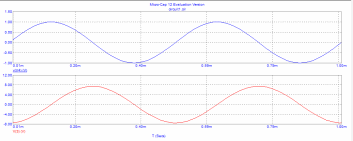
Рис. 13 - зависимости напряжений на входе u1(t)=V(V1) и выходе u2(t)=V(2)
дифференцирующей цепи от времени t.
Ответы на вопросы
1) Какие цепи являются интегрирующими? Приведите пример.
Интегрирующие цепи – такие цепи, у которых выходное напряжение пропорционально интегралу входного напряжения.
Пример:
Нелинейный интегратор.
Фильтр нижних частот.
Линии задержки сигналов.
2) Какие цепи являются дифференцирующими? Приведите пример.
Дифференцирующие цепи – такие цепи, у которых выходной сигнал прямо пропорционален производной входного сигнала.
Пример:
Фильтр верхних частот.
3) В каких случаях применяются интегрирующие цепи?
Интегрирующие цепи применяют для выполнения операций интегрирования в аналоговых вычислительных устройствах.
4) В каких случаях применяются дифференцирующие цепи?
Дифференцирующие цепи применяют тогда, когда требуется преобразовать входное напряжение в сигнал, изменяющийся по закону производной входного напряжения.
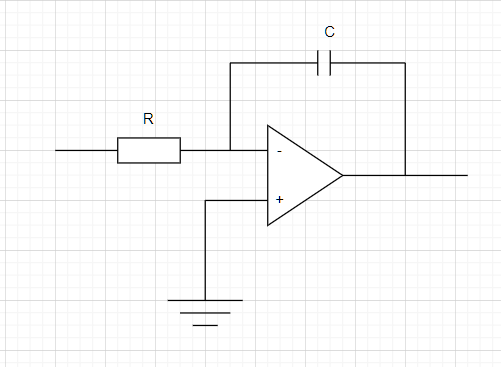
5) Нарисуйте схему интегратора на ОУ и выведите его передаточную функцию Н?
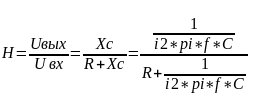
6) Нарисуйте схему дифференциатора на ОУ и выведите его передаточную функцию Н?
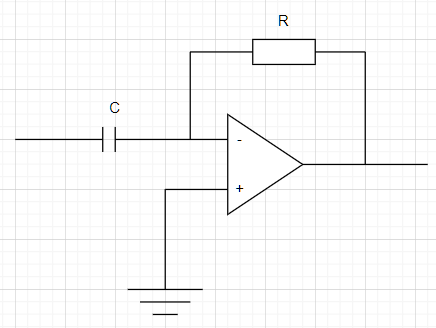
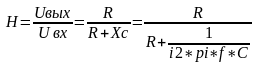
+
