Файл: Лабораторная работа Сравнительная эффективность метода ДормандаПринса в классическом и параллельном вариантах реализации.docx

Титульный лист

Оглавление

Лабораторная работа №

«Сравнительная эффективность метода Дорманда-Принса в классическом и параллельном вариантах реализации»

Цель работы

взять из методички

Задание на лабораторную работу

взять из методички

Ход выполнения

В числовом анализе метод Дорманда – Принса (RKDP) или метод DOPRI , является явным методом решения обыкновенных дифференциальных уравнений, разработанный Дормандом и Принсем в 1980 году. Метод является членом семейства решателей ODE Рунге – Кутта. В частности, он использует шесть оценок функций для вычисления решений четвертого и пятого порядков. Тогда разность между этими решениями принимается за ошибку решения (четвертого порядка). Эта оценка ошибки очень удобна для алгоритмов интеграции с адаптивным размером шага. Другие аналогичные методы интеграции: Фельберг (RKF) и Кэш – Карп (RKCK).

Метод Дорманда – Принса состоит из семи этапов, но он использует только шесть вычислений функций на шаг, поскольку он имеет свойство FSAL (первый такой же, как последний): последний этап оценивается в той же точке, что и первый этап. следующего шага. Дорманд и Принс выбрали коэффициенты своего метода, чтобы минимизировать ошибку решения пятого порядка. В этом основное отличие от метода Фельберга, который был построен таким образом, что решение четвертого порядка имеет небольшую ошибку. По этой причине метод Дорманда – Принса более подходит, когда для продолжения интеграции используется решение более высокого порядка, практика, известная как локальная экстраполяция.

Метод Дорманда-Принса в настоящее время является методом по умолчанию в решателе ode45 для MATLAB и GNU Octave и является выбором по умолчанию для решателя проводника модели Simulink . Это опция в библиотеке интеграции ODE от Scipy. Также доступны реализации для языков программирования Fortran, Java и C ++ .

Коэффициенты, используемые в методе Дорманда-Принса, представлены в таблице:



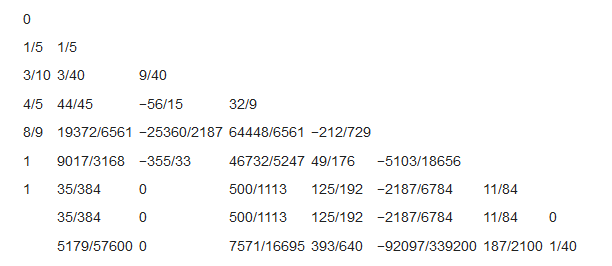
Первая строка коэффициентов b дает решение пятого порядка точности, а вторая строка дает альтернативное решение, которое при вычитании из первого решения дает оценку ошибки.

---

Одноэтапный расчет в методе Дорманда-Принса выполняется следующим образом:



Тогда значение следующего шага yk+1 вычисляется как



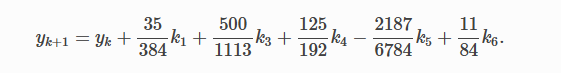
Это вычисление методом Рунге-Кутты четвертого порядка. Мы должны знать, что мы не используем k2, хотя оно используется для вычисления k3 и так далее.

Далее мы вычислим значение следующего шага zk+1 методом Рунге-Кутты порядка 5 как



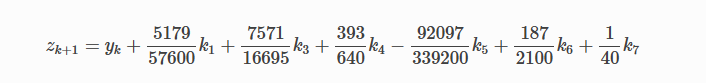
Рассчитываем разницу двух следующих значений |zk+1−yk+1|.



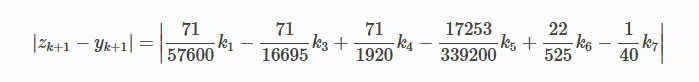
Это считается ошибкой в yk+1. Мы вычисляем оптимальный интервал времени hopt как,



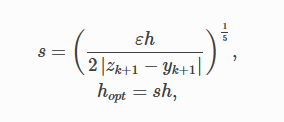
где h в правой части - старый интервал времени. В практическом программировании этот новый hopt будет использоваться на следующем этапе расчета, хотя автор считает, что его также следует использовать в текущих расчетах, когда он очень мал, например, наполовину или меньше.

Параллельное программирование применяется тогда, когда для последовательной программы требуется уменьшить время ее выполнения, или когда последовательна программа, в виду большого объема данных, перестает помещаться в память одного компьютера. Направление развития в области высокопроизводительных вычислений как раз направлено на решение этих двух задач: создание мощных вычислительных комплексов с большим объемом оперативной памяти с одной стороны и разработка соответствующего ПО с другой.

По сути весь вопрос заключается в минимизации соотношения цена/производительность. Ведь всегда можно построить (собрать) вычислительную систему, которая будет эффективно решать поставленную задачу, но адекватна ли будет при этом цена такого решения. Можно выделить два направления развития компьютерной техники: векторные машины (Cray) и кластеры (обычные компьютеры, стандартное ПО).

В массе своей все вычислительные комплексы и компьютеры делятся на три группы:

• 
  Системы с распределенной памятью. Каждый процессор имеет свою память и не может напрямую доступаться к памяти другого процессора. Разрабатывая программы подобные системы, программист в явном виде должен задать всю систему коммуникаци (Передача сообщений – Message Passing). Библиотеки: MPI, PVM, Shmem (Cray only).
  
• 
  Системы с общей (разделяемой) памятью. Процессор может напрямую обращаться в память другого процессора. Процессоры могут сидеть на одной шине (SMP). Разделяемая память может быть физически распределенной, но тогда стоимость доступа к удаленной памяти может быть очень высока и это должен учитывать разработчик ПП. Подходы к разработке ПО: Threads, директивы компилятора (OpenMP), механизм передачи
  сообщения.
  
• 
  Комбинированные системы. В кластерах могут объединяться компьютеры различной конфигурации.
  

---

Для реализации параллельного выполнения программы в рамках текущей лабораторной работы была выбрана библиотека OpenMP.

OpenMP – механизм написания параллельных программ для систем с общей памятью. Состоит из набора директив компилятора и библиотечных функций.
Позволяет достаточно легко создавать многопоточные приложения на С/С++, Fortran. Поддерживается производителями аппаратуры (Intel, HP, SGI, Sun, IBM), разработчиками компиляторов (Intel, Microsoft, KAI, PGI, PSR, APR, Absoft).

Стандарт Open MP был основан на языке Fortran в 1997 г., но позднее в 1998 г. включил в себя и языки C/C++. На данный момент уже доступна версия 5.2. Разработкой OpenMP занимается ARB (Architecture Review Board). ARB - это некоммерческая организация, в ёё состав входят крупнейшие разработчики SMP-архитектур и ПО.

Программа, созданная с применением технологии OpenMP, состоит из последовательных (однопоточных) и параллельных (многопоточных) участков. В OpenMP используется модель распараллеливания «Ветвление - Слияние». Вначале иметься только единственный поток его называют начальным потоком или ещё основной нитью (Master thread, здесь threard это легковесные процессы). Как только поток встречает параллельную конструкцию в коде программы, он создает группу потоков и становится главным потоком. В созданной группе все потоки, включая главный, выполняют код программы. После выполнения параллельной конструкции в коде, работу продолжает только главный поток.



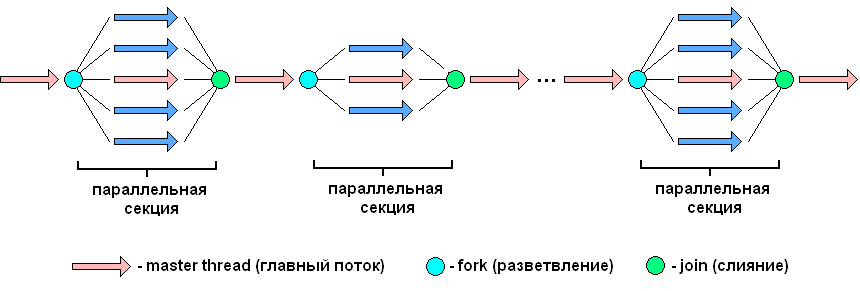
Число потоков выполняющие параллельную часть можно контролировать по разному, можно использовать OMP_NUM_THREADS или вызвать процедуру omp_set_num_threads().

Память в OpenMP разделяется на: локальную и общую память. Локальная память доступна только для одной нити, а общая, для нескольких.

Основные возможности и положительные качества технологии распараллеливания OpenMP:

1. 
   В OpenMP дается возможность реализовать максимально эффективно многопроцессорные вычислительные системы с общей памятью, позволяя использовать общие данные для параллельно выполняемых потоков, без каких либо затруднений для межпроцессорных передач данных.
   
2. 
   В OpenMP дается возможность инкрементной (поэтапной) разработки параллельных программ. Это значит, что на ранних этапах разработки мы уже можем получить параллельную программу, достигается это благодаря директивам OpenMP, они могут добавляться в последовательную программу поэтапно.
   
3. 
   В OpenMP снижена вероятность возникновения проблем при переносе параллельных программ между разными компьютерами. Программа, написанная на языке C или Fortran с использованием технологии OpenMP, будет выполняться для разных вычислительных систем с общей памятью.
   
4. 
   В OpenMP простой набор директив для изучения. И разработка сравнительно простых параллельных программ не требует больших усилий, иногда достаточно добавить пару директив в последовательную программу. Но не стоит забывать, что при разработке сложных программ требуется соответствующие знания.
   

---

Кратко рассмотрим структуру OpenMP. В составе OpenMP можно выделить:

· Директивы

· Функции

· Переменные окружения

Директивы.

В общем виде формат директив можно представить в виде:
#pragma omp <Имя директивы> [<параметр>[[,] <параметр>]…]
Где #pragma omp <Имя директивы> это фиксированная часть, а параметром может быть хоть сколько угодно.

Основные директивы:

· parallel – используется для выделения параллельной области

· for – используется для автоматического распараллеливания циклов

Приведем общий вид для этих двух директив:

#pragma omp parallel[<параметр>[[,] <параметр>]…]

<код программы>

#pragma omp for[<параметр>[[,] <параметр>]…]

<Цикл for>

Основные функции:

· omp_get_num_threads() – узнать, сколько потоков в текущей параллельной области

· omp_get_thread_num() – узнать номер текущей нити (все нити нумеруются с 0).

· Функции управления свойствами параллельных областей:

(1) omp_set_nested(true|false),

(2)omp_set_dynamic(true|false)

Переменные окружения:

· OMP_DYNAMIC – значение говорит о том, разрешено ли программе менять количество процессов динамически.

· OMP_NUM_THREADS – количество процессов в параллельной области по умолчанию, и пр.

Для использования OpenMP нужно скомпилировать программу компилятором, поддерживающим OpenMP. В данной лабораторной работе использовался компилятор C++ от компании Microsoft, входящий в состав среды разработки Visual Studio 2019.

Компилятор интерпретирует директивы OpenMP и создаёт параллельный код. При использовании компиляторов, не поддерживающих OpenMP, директивы OpenMP игнорируются без дополнительных сообщений. Компилятор с поддержкой OpenMP определяет макрос_OPENMP, который может использоваться для условной компиляции отдельных блоков, характерных для параллельной версии программы. Этот макрос определён в формате yyyymm, где yyyy и mm – цифры года и месяца, когда был принят поддерживаемый стандарт OpenMP.



Результат выполнения программы представлен на рисунке:



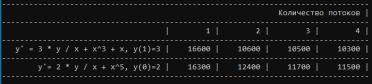
Выполнение программы производилось на количестве ядер от 1 до 4. Время выполнения указано в наносекундах.



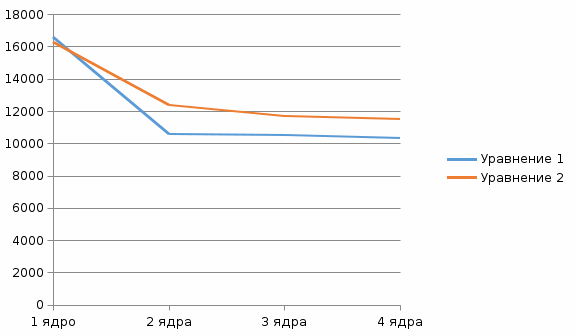
График зависимости времени выполнения от количества используемых процессорных ядер

---

Листинг программы

#include

#include

#include

#include

#include

#include
bool dorpi(double (*f)(double, double), double* y, double x, double h, double xmax) {
int attempts = 12;

double tolerance = 1.e-5;

double eps = 1.e-9;

double min_scale_factor = 0.125;

double max_scale_factor = 4.0;
double h_next, scale, err, yy, temp_y[2], k1, k2, k3, k4, k5, k6, k7, h5;

const double r_45 = 1.0 / 45.0,

r_8_9 = 8.0 / 9.0,

r_6561 = 1.0 / 6561.0,

r_167904 = 1.0 / 167904.0,

r_142464 = 1.0 / 142464.0,

r_21369600 = 1.0 / 21369600.0;
int i, last_interval = 0;
if (xmax < x || h <= 0.0) return false;
h_next = h;

y[1] = y[0];

if (xmax == x) return true;
h = std::min(h, xmax - x);
tolerance /= (xmax - x);
temp_y[0] = y[0];
#pragma omp parallel

while (x < xmax) {

scale = 1.0;

for (i = 0; i < attempts; i++) {

// Runge-Kutta Method //

h5 = 0.2 * h;

k1 = (*f)(x, *temp_y);

k2 = (*f)(x + h5, *temp_y + h5 * k1);

k3 = (*f)(x + 0.3 * h, *temp_y + h * (0.075 * k1 + 0.225 * k2));

k4 = (*f)(x + 0.8 * h, *temp_y + r_45 * h * (44.0 * k1 - 168.0 * k2 + 160.0 * k3));

k5 = (*f)(x + r_8_9 * h, *temp_y + r_6561 * h * (19372.0 * k1 - 76080.0 * k2 + 64448.0 * k3 - 1908.0 * k4));

k6 = (*f)(x + h, *temp_y + r_167904 * h * (477901.0 * k1 - 1806240.0 * k2 + 1495424.0 * k3 + 46746.0 * k4 - 45927.0 * k5));

k7 = (*f)(x + h, *temp_y + r_142464 * h * (12985.0 * k1 + 64000.0 * k3 + 92750.0 * k4 - 45927.0 * k5 + 18656.0 * k6));

*(temp_y + 1) = *temp_y + r_21369600 * h * (1921409.0 * k1 + 9690880.0 * k3 + 13122270.0 * k4 - 5802111.0 * k5 + 1902912.0 * k6 + 534240.0 * k7);

err = fabs(r_21369600 * (26341.0 * k1 - 90880.0 * k3 + 790230.0 * k4 - 1086939.0 * k5 + 895488.0 * k6 - 534240.0 * k7));
if (err < eps) { scale = max_scale_factor; break; }

yy = (fabs(temp_y[0]) < eps) ? tolerance : fabs(temp_y[0]);

scale = 0.8 * sqrt(sqrt(tolerance * yy / err));

scale = std::min(std::max(scale, min_scale_factor), max_scale_factor);

if (err < (tolerance * yy)) break;

h *= scale;

if (x + h > xmax) h = xmax - x;

else if (x + h + 0.5 * h > xmax) h = 0.5 * h;

}

if (i >= attempts) { h_next = h * scale; return -1; };

temp_y[0] = temp_y[1];

x += h;

h *= scale;

h_next = h;

if (last_interval) break;

if (x + h > xmax) { last_interval = 1; h = xmax - x; }

else if (x + h + 0.5 * h > xmax) h = 0.5 * h;

}

y[1] = temp_y[1];

return true;

}
double equation1(double x, double y) {

return 3.0 * y / x + pow(x, 3) + x;

}
double equation2(double x, double y) {

return 2.0 * y / x + pow(x, 5);

}
int main() {

const char delimiter[] = "---------------------------------------------------------------------------------";
setlocale(LC_ALL, "");
std::cout << delimiter << std::endl;

std::cout << std::setw(79) << "Количество потоков" << std::setw(2) << '|' << std::endl;

std::cout << delimiter << std::endl;
for (int i = 0; i < 5; i++) {

if (i > 0)

std::cout << std::setw(9) << i << std::setw(2) << '|';

else

std::cout << std::setw(37) << '|';

}

std::cout << std::endl;
std::cout << delimiter << std::endl;
int threads_count = 1;
std::cout << std::setw(35) << "y' = 3 * y / x + x^3 + x, y(1)=3" << std::setw(2) << '|';
while (threads_count < 5) {

omp_set_num_threads(threads_count);
auto begin = std::chrono::steady_clock::now();
double* y = new double[2];

double x0, x, h;

bool is_solved;
x0 = 1; y[0] = 3;
x = 2.0;
h = 0.01;
is_solved = dorpi(equation1, y, x0, h, x);
delete[] y;
auto end = std::chrono::steady_clock::now();
auto elapsed_ns = end - begin;
if (is_solved)

std::cout << std::setw(9) << elapsed_ns.count() << std::setw(2) << '|';

else

std::cout << std::setw(9) << "Not solved" << std::setw(2) << '|';
threads_count++;

}
std::cout << std::endl << delimiter << std::endl;
threads_count = 1;
std::cout << std::setw(35) << "y'= 2 * y / x + x^5, y(0)=2" << std::setw(2) << '|';
while (threads_count < 5) {

omp_set_num_threads(threads_count);
auto begin = std::chrono::steady_clock::now();
double* y = new double[2];

double x0, x, h;

bool is_solved;
x0 = 0; y[0] = 2;
x = 2.0;
h = 0.01;
is_solved = dorpi(equation2, y, x0, h, x);

delete[] y;
auto end = std::chrono::steady_clock::now();
auto elapsed_ns = end - begin;
if (is_solved)

std::cout << std::setw(9) << elapsed_ns.count() << std::setw(2) << '|';

else

std::cout << std::setw(9) << "Not solved" << std::setw(2) << '|';
threads_count++;

}
std::cout << std::endl << delimiter << std::endl;

return 0;

}

Вывод

В ходе выполнения лабораторной работы был изучен метод Дорманда-Принса для решения обыкновенных дифференциальных уравнений. Также была изучена библиотека параллельных вычислений OpenMP. В результате выполнения лабораторной работы была реализована программа на языке программирования С++ с использованием библиотеки OpenMP, реализующая метод Дорманда-Принса. Было произведено сравнение времени выполнения алгоритма при работе от 1 до 4 параллельных потоков.

Список литературы

1. 
   Антонов А.С. Параллельное программирование с использованием технологии OpenMp. – М.: Изд-во МГУ, 2009. – 77 с
   
2. 
   Малышкин В.Э. Параллельное программирование мультикомпьютеров, Новосибирск, 2006. – 452 с
   
3. 
   Бахтин А.В. Технология параллельного программирования OpenMP, Москва, 2012. – 125 с
   
4. 
   Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. – СПб.:
   
5. 
   БХВ-Петербург, 2002.
   
6. 
   Chandra, R., Dagum, L., Kohr, D., Maydan, D., McDonald, J., and Melon, R.(2000). Parallell Programming in OpenMP. San-Francisco, CA: Morgan Kaufmann Publishers.
   
7. 
   Quinn, M. J. (2004). Parallel Programming in C with MPI and OpenMP. – New York, NY: McGraw-Hill.
   
8. 
   Гергель В.П. Параллельное программирование с использованием
   
9. 
   OpenMP, Новосибирск, 2007. – 33с
   
10. 
    Параллельные заметки. URL: http://habrahabr.ru/company/intel/blog/82486
    
11. 
    Лабораторная работа. Компиляция и запуск программ. URL:http://gigabaza.ru/doc/106635.html
    
12. 
    OpenMP Compilers. – URL: http://openmp.org/wp/openmp-compilers/
    
13. 
    Analyzing the Effect of Different Programming Models Upon Performance and Memory Usage on Cray XT5 Platforms
    URL: https://www.nersc.gov/assets/NERSC-Staff-Publications/2010/Cug2010Shan.pdf
    

---