Файл: Задача Найти матрицу, обратную матрице . Решение. Найдем определитель матрицы., значит, существует.doc
Добавлен: 19.03.2024
Просмотров: 9
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА
Задача 1. Найти матрицу, обратную матрице
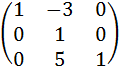.Решение.
Найдем определитель матрицы.
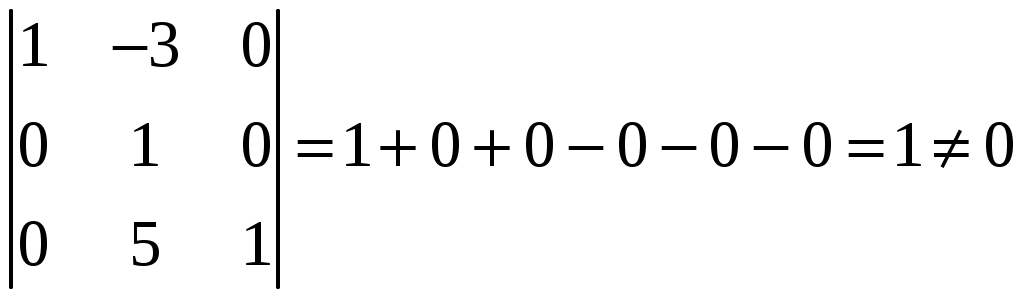, значит, 
существует.
. Составим 
.
; 
; 
; 
; 
; 
; 
; 
; 
. 
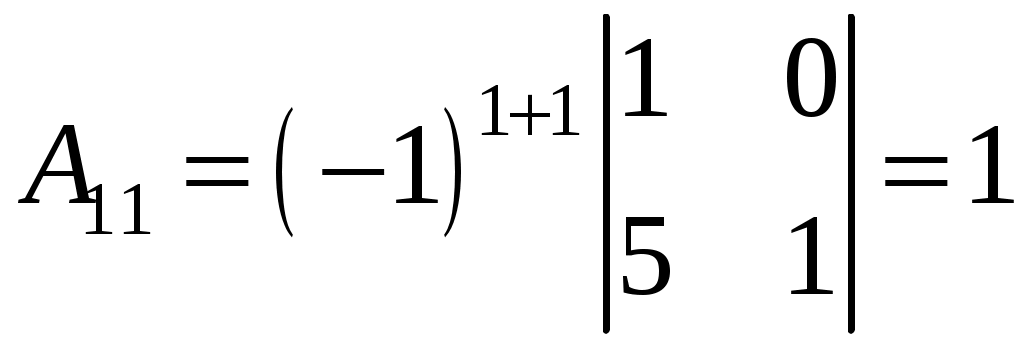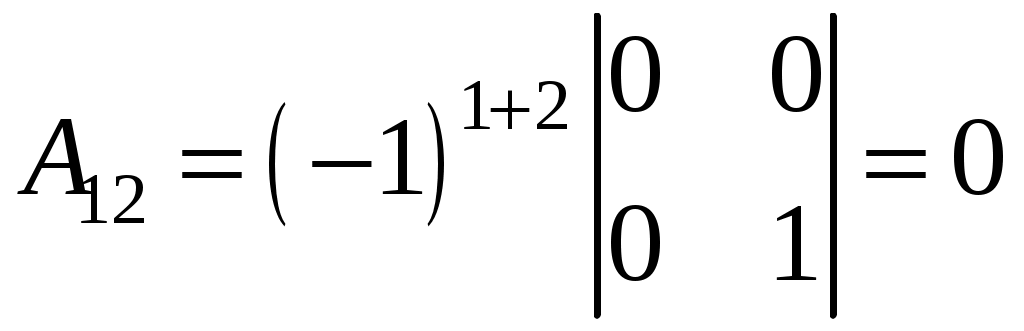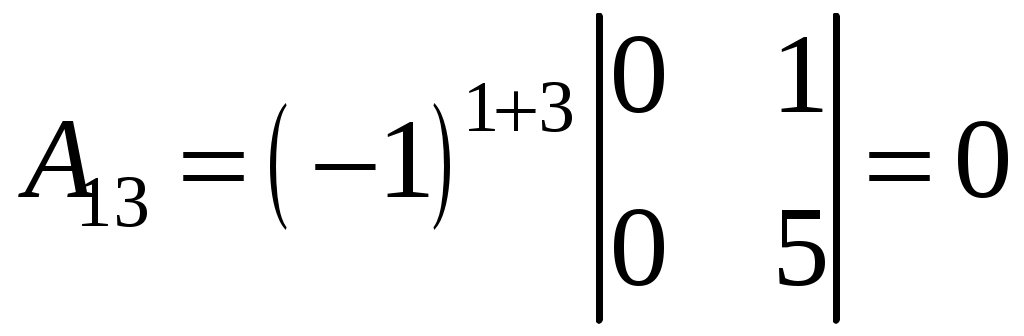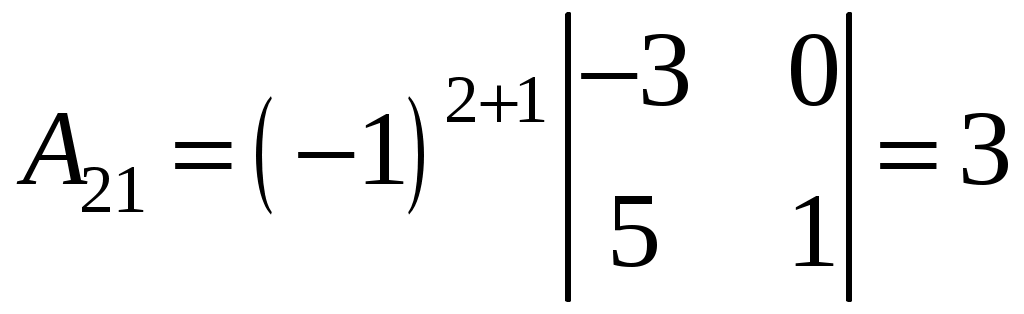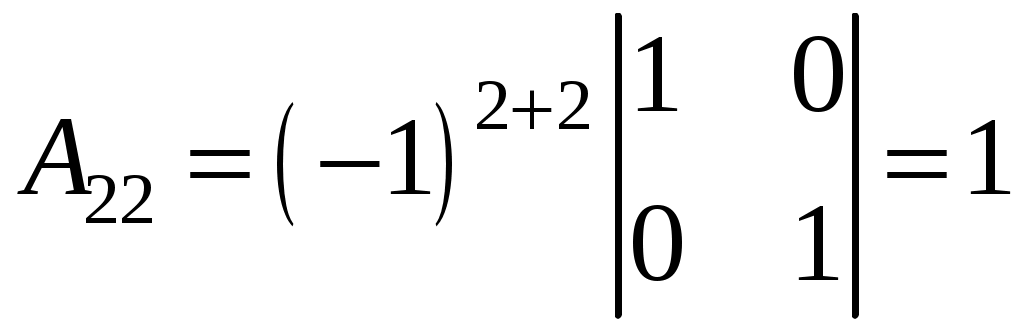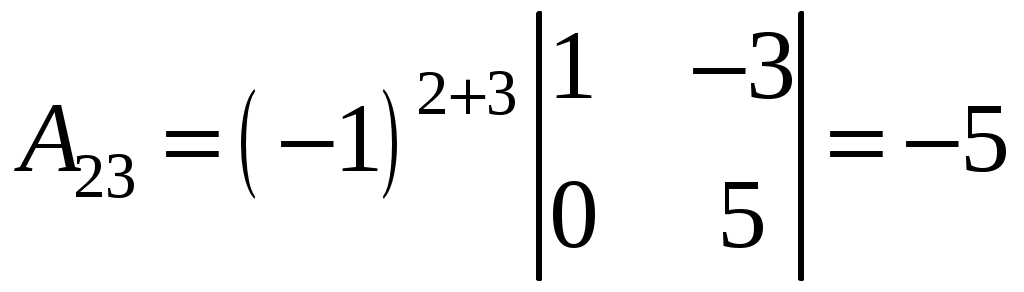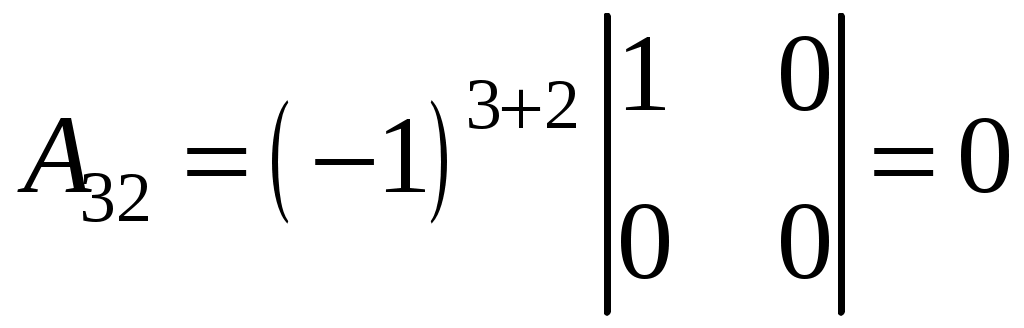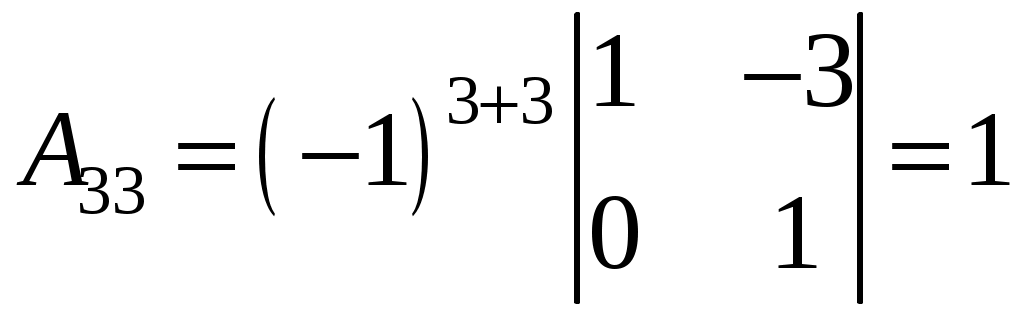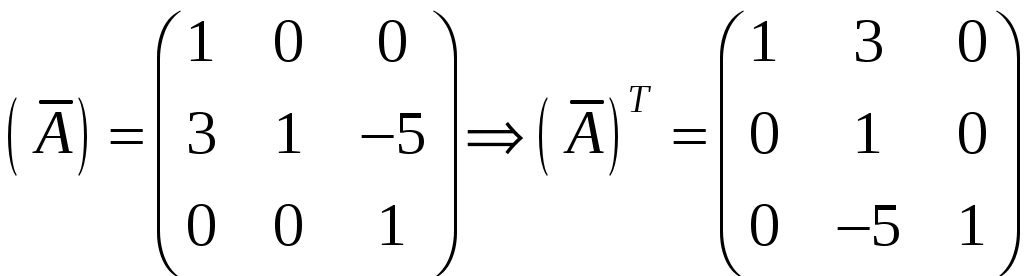, значит,
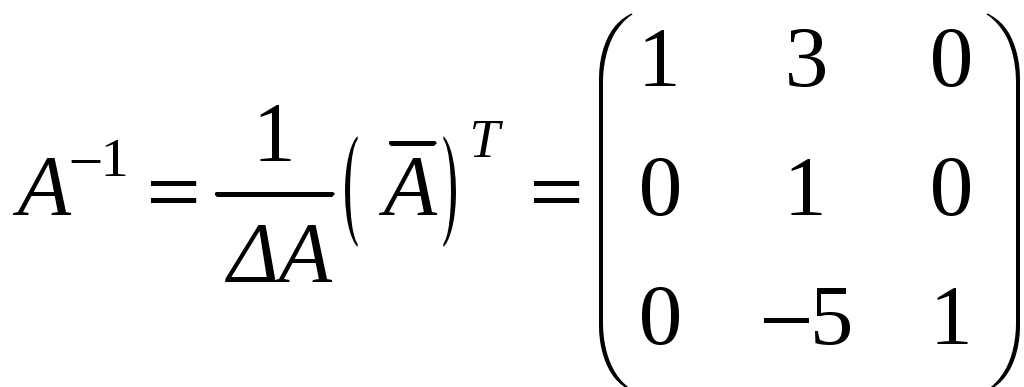. Задача 2.Решить СЛАУ
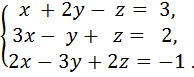
Решение.
Решим систему методом Гаусса.
Умножим первое уравнение системы на -3 и прибавим ко второму, а затем умножим первое уравнение на -2 и прибавим к третьему, получим:
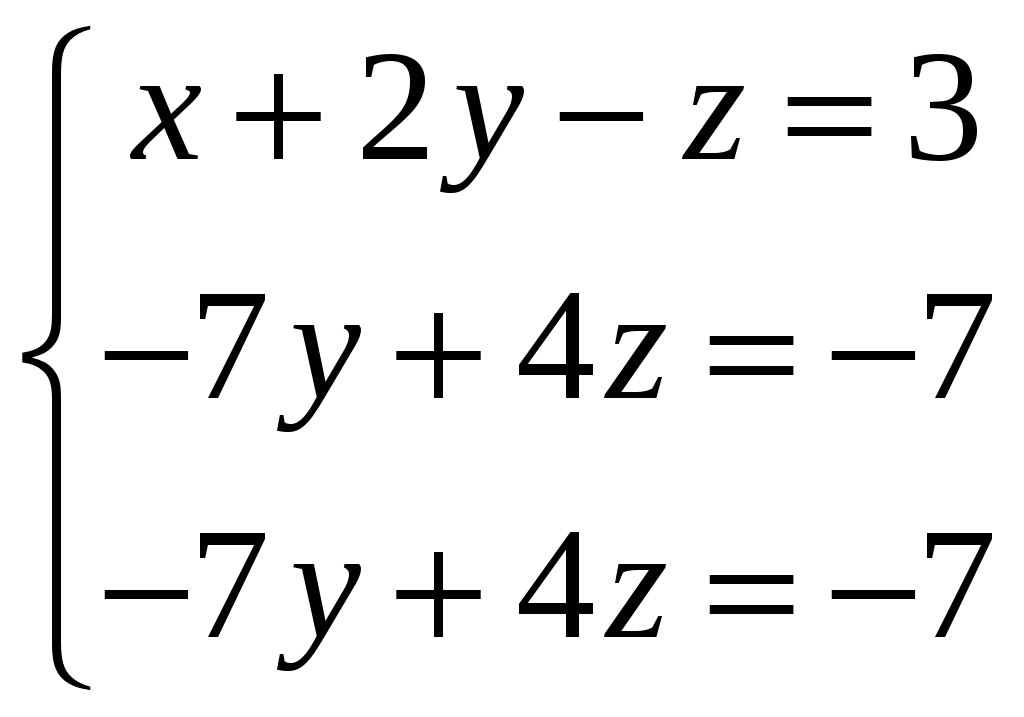.Второе уравнение системы вычтем из третьего, получим:
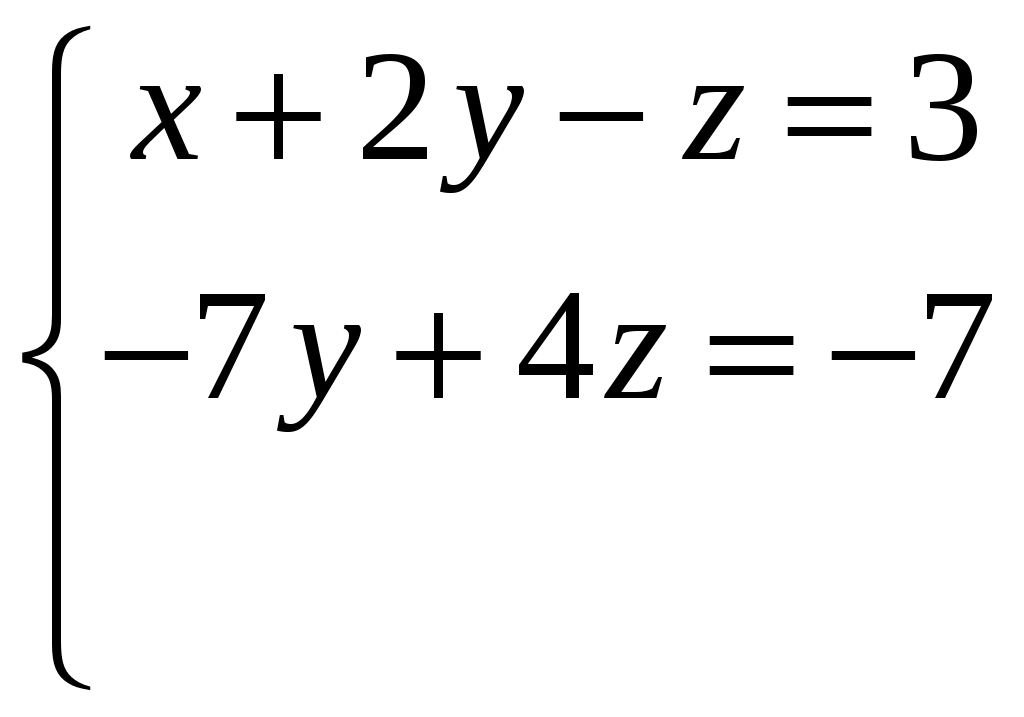
Выбирая в качестве свободной переменной z, выразим из первого и второго уравнения переменные х и у, получим общее решение системы
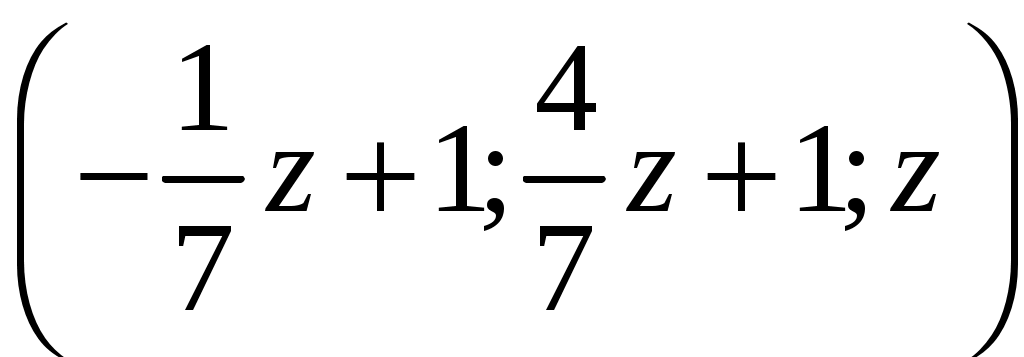
Задача 3.Вероятность того, что в результате проверки изделию будет присвоен «Знак высшего качества», равна 0,2. На контроль поступило 9 изделий. Какова вероятность того, что знак высшего качества будет присвоен:
а) ровно 6-ти изделиям;
б) более чем 7-ми изделиям;
в) хотя бы одному изделию;
г) указать наивероятнейшее число изделий, получивших знак высшего качества, и найти соответствующую ему вероятность.
Решение.
а) Имеем n=9, k=6 p=0,2, применим формулу Бернулли, получим:
,б) Имеем n=9, k>7 p=0,2, применим формулу Бернулли, получим:
в) Имеем n=9, k≥ p=0,2, применим формулу Бернулли, получим
г) Наивероятнейшее число найдем из неравенства:
, получим: 
.
