ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.03.2024
Просмотров: 27
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ
КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра «Теории Электрических Цепей»
Лабораторная работа №14
на тему
«Исследование КИХ-фильтров»
по дисциплине
«Основы компьютерного анализа электрических цепей»
Выполнил: студент гр. БИН2105 Астахов Андрей.
Проверил: Елисеев С. Н.
Москва, 2022
Цель работы: С помощью программы Micro-Cap получить основные временные и частотные характеристики фильтров с конечной импульсной характеристикой(КИХ-фильтров).
Предварительный рассчёт
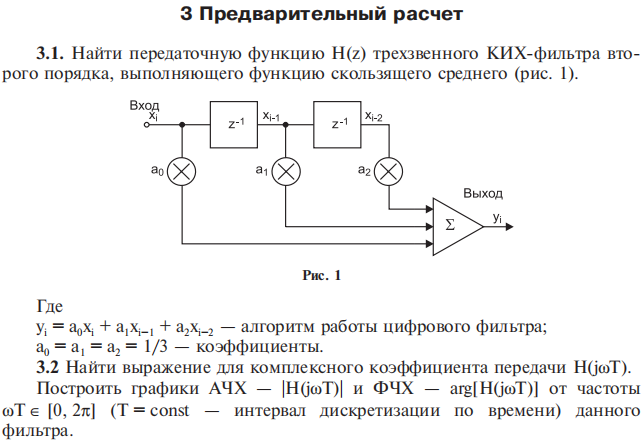
Порядок выполнения работы
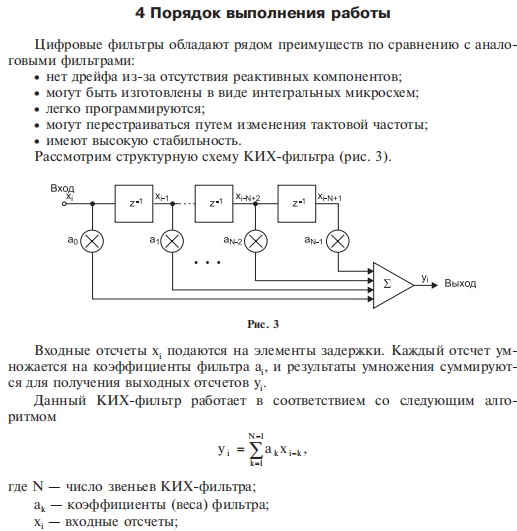
Передаточная функция КИХ-фильтра H(z):
H(z) = a0 + a1z-1 + a2z-2 + … + aN-1z-(N-1) =
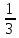(1 + z-1 + z-2)Частотный коэффициент передачи H(jωT) = a0 + a1e-jωT + a2e-2jωT + … + aN-1e-j(N-1)ωT
H(jωT) =
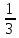(1 + e-jωT + e-2jωT)АЧХ и ФЧХ КИХ-фильтра
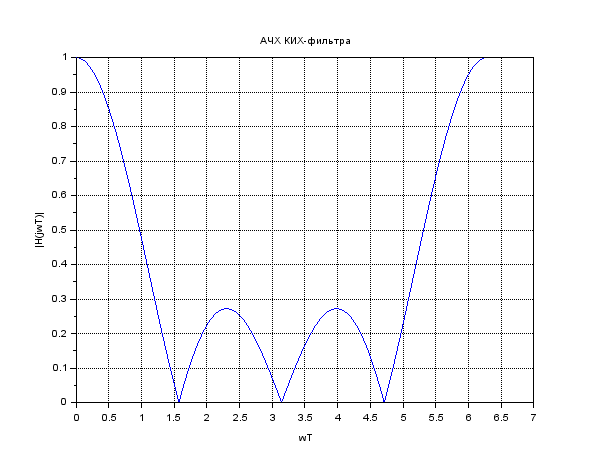
Рисунок 4. АЧХ КИХ-фильтра
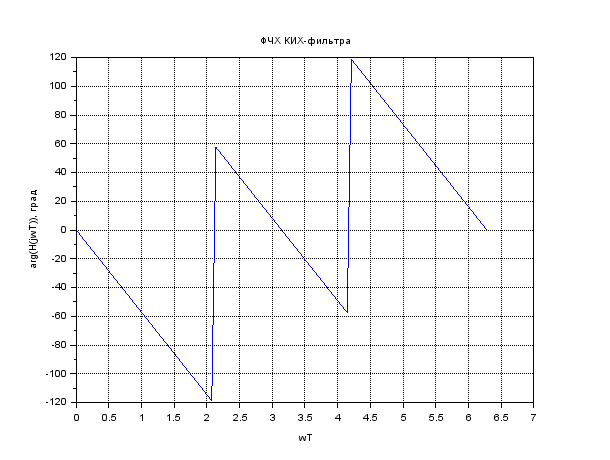
Рисунок 5. ФЧХ КИХ-фильтра
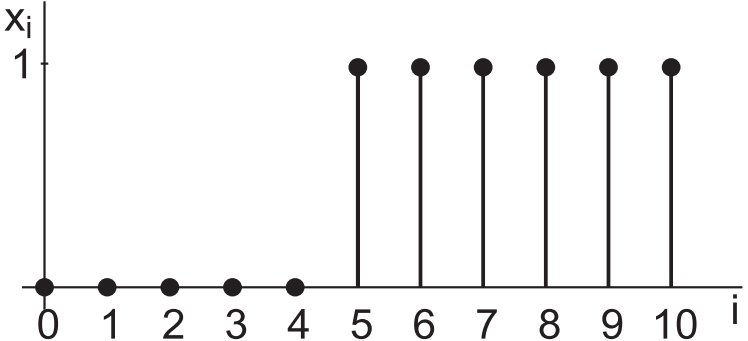
СтРисунок 6.Ступенчатое воздействие
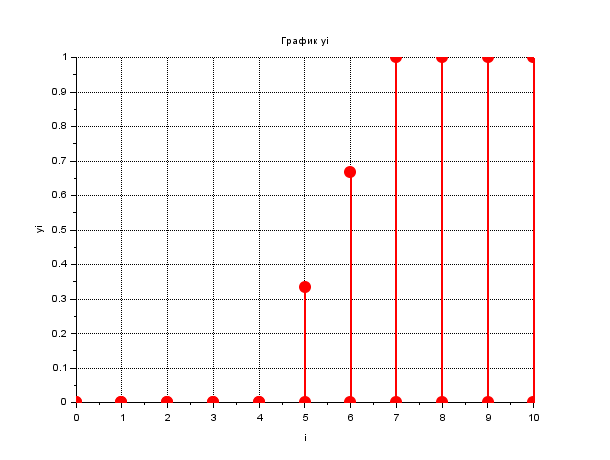
Рисунок 7.График yi.
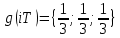
График импульсной характеристики g(iT)
Рисунок 8.
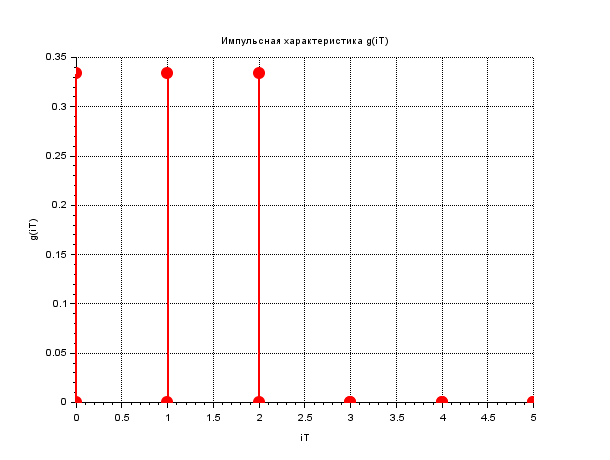— Импульсная характеристика g(iT)Трёхзвенный КИХ-фильтр
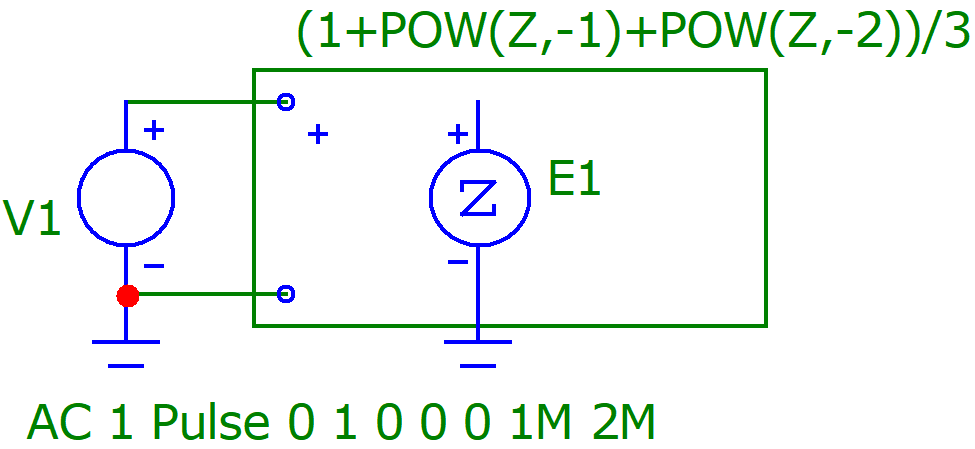
Рисунок 9.Схема Трёхзвенного КИХ-фильтра
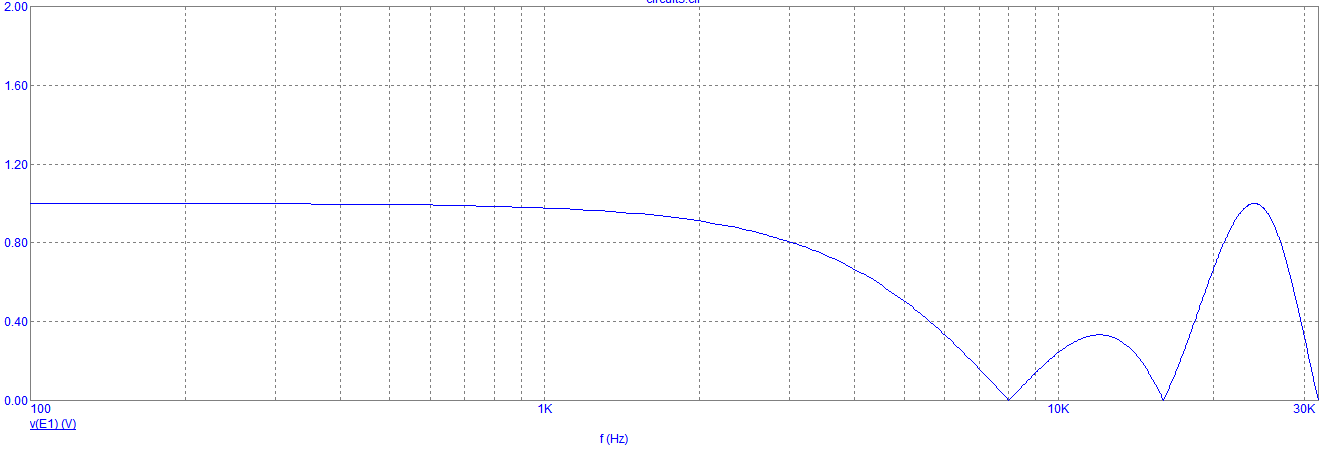
Рисунок 10.АЧХ трехзвенного КИХ-фильтра
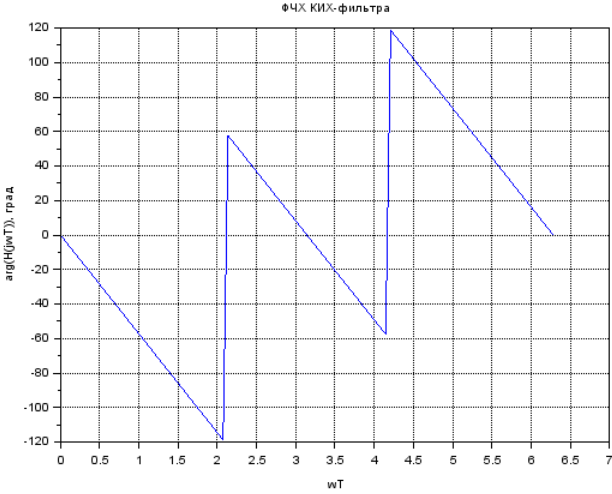
Рисунок 11.ФЧХ трехзвенного КИХ-фильтра
Четырёхзвенный КИХ-фильтр
Передаточная функция H(z):
H(z) = a0 + a1z-1 + a2z-2 + … + aN-1z-(N-1) =
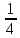(1 + z-1 + z-2 + z-3)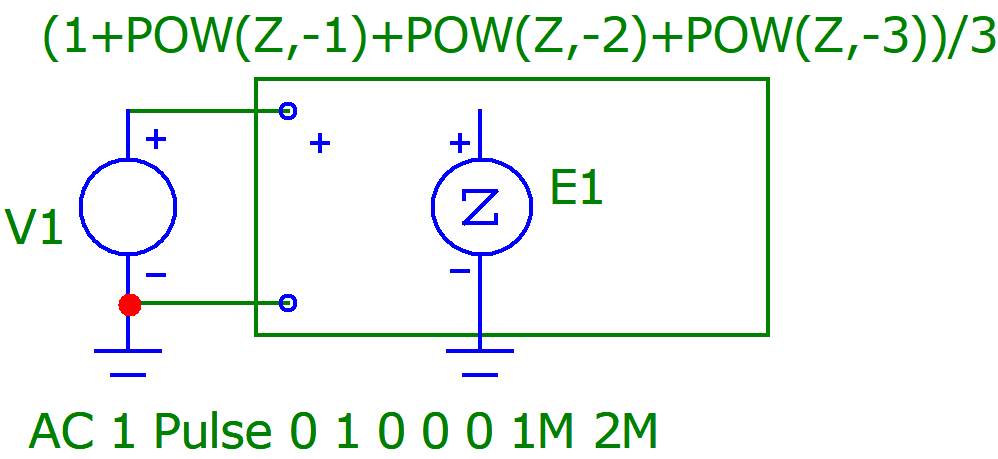
Рисунок 12.Схема Четырёхзвенного КИХ-фильтра
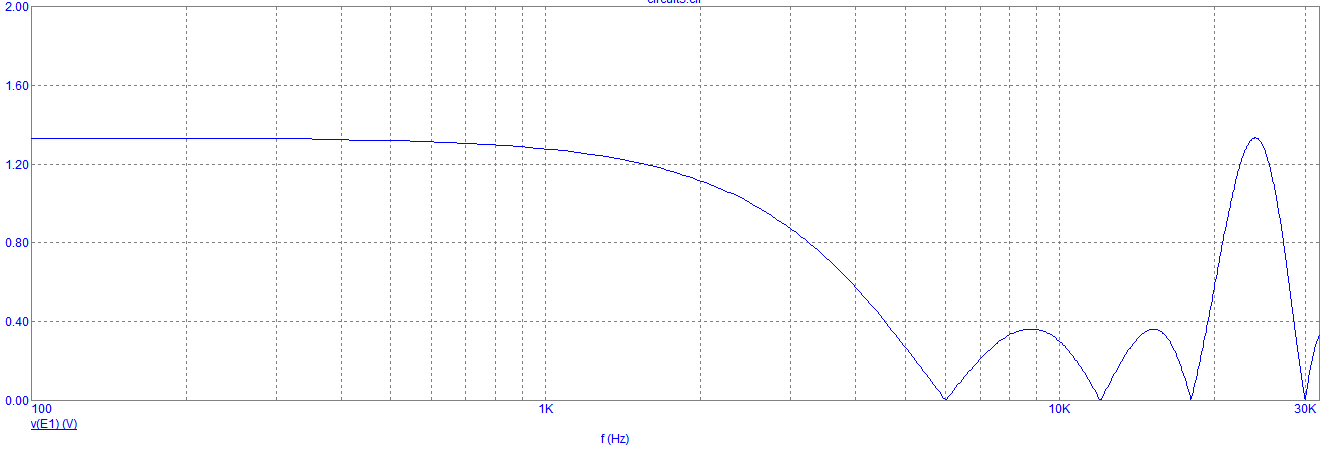
Рисунок 13.АЧХ Четырёхзвенного КИХ-фильтра
Рисунок 14.ФЧХ Четырёхзвенного КИХ-фильтра
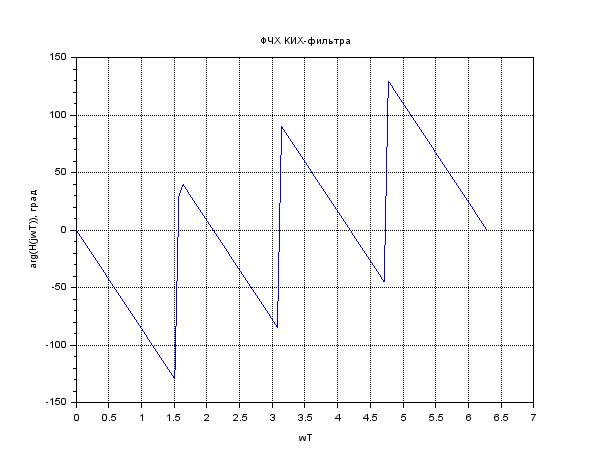
Пятизвенный КИХ-фильтр
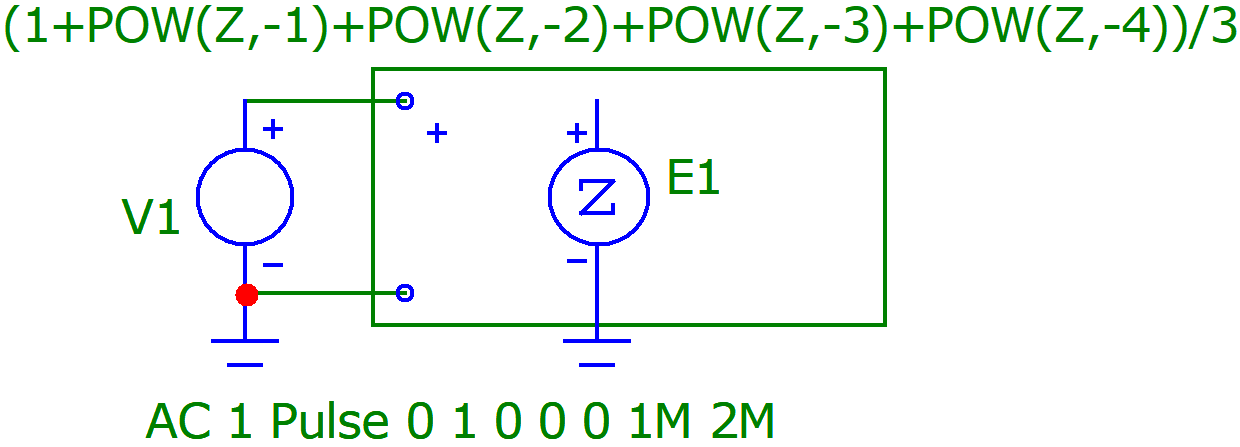
Рисунок 15.Схема Пятизвенного КИХ-фильтра
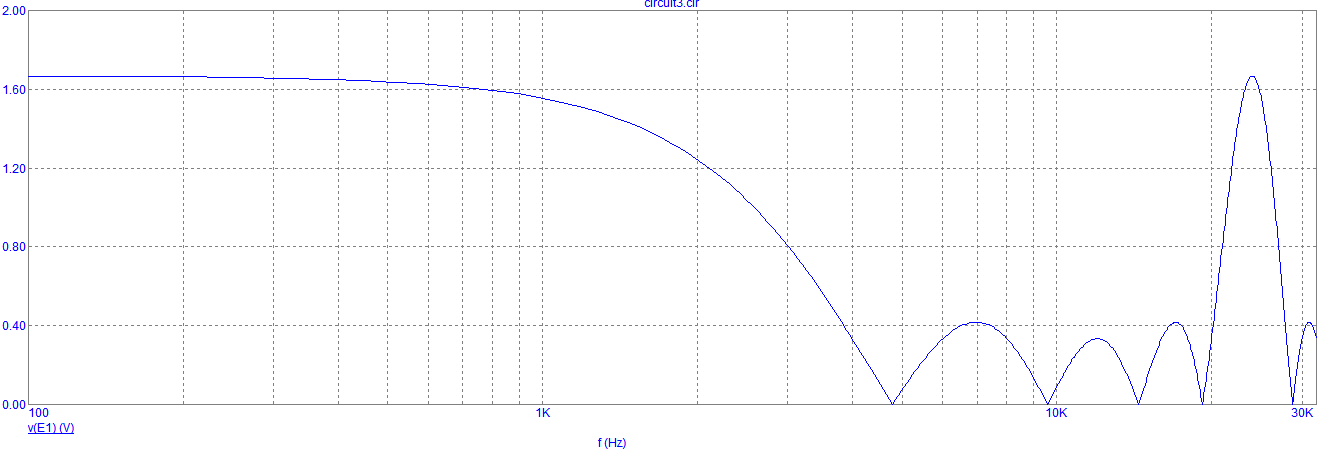
Рисунок 16.АЧХ Пятизвенного КИХ-фильтра
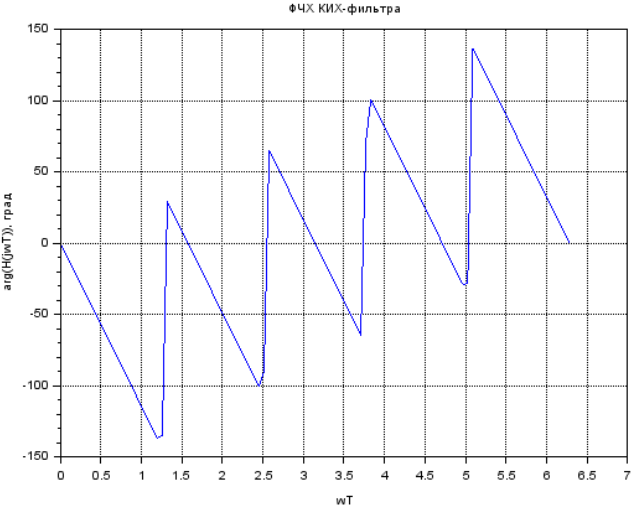
Рисунок 17.ФЧХ Пятизвенного КИХ-фильтра
Вывод:
В данной лабораторной работе с помощью программы Micro-Cap были получены основные временные и частотные характеристики фильтров с конечной импульсной характеристикой (КИХ-фильтров). Были получены АЧХ фильтра, с разным количеством звеньев. (Из графиков видно, что, чем больше мы используем отсчётов нашего фильтра (а количество отсчётов – это порядок цифрового фильтра), тем более его характеристика становится похожа на идеальную.)Из графиков видно что чем большее количестов звеньев мы используем тем лучше “сглаживается” сигнал
Вопросы:
-
Что называется z-преобразованием?
Z-преобразованиемназывают свёртывание исходного сигнала, заданного последовательностью вещественных чисел во временно́й области, в аналитическую функцию комплексной частоты. Если сигнал представляет импульсную характеристику линейной системы, то коэффициенты Z-преобразования показывают отклик системы на комплексные экспоненты.
2)Какими свойствами обладает z-преобразование?
Важнейшим свойством z-преобразования является свойство его единственности. Любая последовательность s(k) однозначно определяется z-изображением в области его сходимости, и наоборот, однозначно восстанавливается по z-изображению.
Без углубления в теорию, можно констатировать, что все свойства ДПФ действительны и для z-преобразования. Отметим некоторые из них.
Линейность: Если s(k) = a·x(k)+b·y(k), то S(z) = aX(z)+bY(z). Соответственно, z-преобразование допустимо только для анализа линейных систем и сигналов, удовлетворяющих принципу суперпозиции.
Задержка на n тактов: y(k) = x(k-n).
Y(z) =
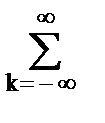y(k) zk = 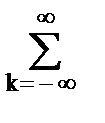x(k-n) zk =zn 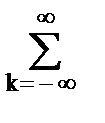x(k-n) zk-n = zn 
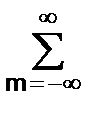x(m) zm = zn X(z).Соответственно, умножение z-образа сигнала на множитель zn вызывает сдвиг сигнала на n тактов дискретизации.
Преобразование свертки. При выполнении нерекурсивной цифровой фильтрации односторонними операторами фильтров:
s(k) =
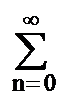h(n) y(k-n), k = 0, 1, 2, …Z-преобразование уравнения свертки:
S(z) =
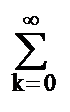
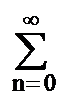h(n) y(k-n) zk =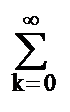
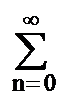
h(n) zn y(k-n) zk-n =
=
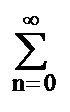h(n) zn 
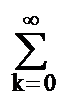y(k-n) zk-n = H(z) Y(z).Таким образом, свертка дискретных функций отображается произведением z-образов этих функций. Аналогично, для z-преобразования могут быть доказаны все известные теоремы о свойствах z-образов, что вполне естественно, т.к. при z=exp(-jw) эти свойства полностью эквивалентны свойствам спектров функций.
Разложение сигналов на блоки последовательной свертки. Z-преобразование позволяет производить разложение сигналов и функций, например передаточных функций фильтров, на короткие составляющие операции свертки, для чего достаточно приравнять z-полином к нулю, найти его корни ai, и переписать полином в виде произведения двучленов:
S(z) = a0(z-a1)(z-a2)...,
где а0- последний отсчет сигнала (коэффициент при старшей степени z).
Но произведению в z-области соответствует свертка в координатной области, и при обратном преобразовании двучлены (z-ai) превращаются в двухточечные диполи {-ai,1}, а сигнал длиной N представляется сверткой (N-1) диполей:
sk= a0{-a1,1}*{-a2,1}*{-a3,1}* ...
Пример. sk = {1.4464, -2.32, 3.37, -3, 1}. S(z) = z4-3z3+3.37z2-2.32z+1.4464. a0 = 1.
Корни полинома S(z): a1 = 0.8+0.8j, a2 = 0.8-0.8j, a3 = 0.7+0.8j, a4 = 0.7-0.8j,
S(z) = (z-0.8-0.8j)(z-0.8+0.8j)(z-0.7-0.8j)(z-0.7+0.8j).
Корни полинома представлены на z-плоскости на рис. 8.1.1. Корни полинома комплексные и четыре двучлена в координатной области также будут комплексными. Но они являются сопряженными, и для получения вещественных функций следует перемножить сопряженные двучлены и получить биквадратные блоки:
S(z) = (z2-1.4z+1.13)(z2-1.6z+1.28).
При переходе в координатную область: sk = {1.13, -1.4, 1} * {1.28, -1.6, 1}.
Таким образом, исходный сигнал разложен на свертку двух трехчленных сигналов (функций).
Дифференцирование. Если имеем s(k) « S(z), то z-образ функции s'(k) можно найти, продифференцировав S(z), что бывает полезно для вычисления обратного z-преобразования функций S(z) с полюсами высокого порядка:
s'(k) « z dS(z)/dz.
3)Какие фильтры называеются цифровыми?
Цифровой фильтр — в электронике любой фильтр, обрабатывающий цифровой сигнал с целью выделения и/или подавления определённых частот этого сигнала.
Классификация фильтров осуществляется по полосе пропускания (ФНЧ, ФВЧ, ПФ, РФ) и по типу фильтра (Баттерворта и Чебышева).
По полосе пропускания:
ФНЧ – аналоговый или электрический фильтр, эффективно пропускающий частотный спектр сигнала ниже частоты среза и уменьшающий частоту спектра сигнала выше этой частоты. Степень подавления зависит от фильтра.
ФВЧ – электрический или другой фильтр, пропускающий высокие частоты спектра входного сигнала, при этом подавляя частоты спектра сигнала меньше, чем частота среза.
Полосовой фильтр – представлен в виде последовательности, состоящей из ФНЧ иФВЧ. ПФ: а) нижняя частота среза; б) верхняя частота среза.
Режекторный фильтр – фильтр, не пропускающий колебания определенной полосы частот.
По типу фильтра:
Фильтр Чебышева – один из типов линейных аналоговых или цифровых фильтров, отличительной особенностью которых является более крутой спад АЧХ и существенная пульсация АЧХ в полосе пропускания.
Фильтр Баттерворта – один из типов электрических фильтров. Фильтры этого класса отличаются от других фильтров методом проектирования. Фильтр Баттерворта проектируется так, чтобы его АЧХ была максимально гладкой на частотах полосы пропускания.
4)Дайте определение передаточной функции цифрового фильтра?
5)Какие фильтры называются КИХ-фильтрами?
КИХ фильтр — это линейный цифровой фильтр, основной особенностью которого является ограниченность во времени его импульсной характеристики, то есть с определенного момента времени она становится равной нулю. Как правило, большинство КИХ фильтров выполнено без обратной связи, поэтому практически все КИХ фильтры — нерекурсивные
Все КИХ-фильтры описываются следующими уравнениями:
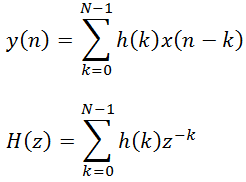
где y(n) — выходной сигнал (функция текущего и прошедших значений на входе), x(n) — входное воздействие, h(k) — коэффициенты импульсной характеристики, N — длина фильтра (количество коэффициентов фильтра), H(z) — передаточная характеристика фильтра.