ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»

Кафедра автоматизации технологических процессов и производств

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №6

По дисциплине: насосно-компрессорное оборудование

Тема работы: экспериментальное изучение уравнения Бернулли

Выполнил: студент гр. АПН-20 /Прохватилов А.Д./

^{(подпись)}

Дата: 25.12.2022
Проверил:

Руководитель работы: ассистент /Лебедик Е.А./

^{(подпись)}
Санкт-Петербург

2022

Цель работы: повышение уровня знаний о «Законе Бернулли» и движении жидкости в трубопроводе.
Теоретические сведения

Основным уравнением гидродинамики является уравнение Бернулли, устанавливающие связь между давлением р, Па жидкости и скоростью её движения w, м/с. Уравнение Бернулли, записанное для двух произвольно взятых сечений элементарной струйки (скорости в различных точках сечение элементарный струйки одинаковы, а сама струйка с течением времени не изменяет своей формы) идеальной несжимаемой жидкости имеет вид:

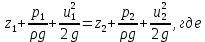
z – геометрический напор, м;

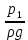– пьезометрический напор, м;

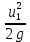– скоростной напор, м;

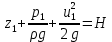называется полным напором, под которым понимают удельную энергию жидкости, отнесенную к единице силы тяжести. Первые два члена представмют собой удельную потенциальную энергию жидкости, а третий член кинетическую энергию. Энергетический смысл уравнения Бернулли заключается в том, что для элементарной струйки идеальной жидкости полный напор, то

---

есть сумма геометрического, пьезометрического и скоростного напоров, есть величина постоянная во всех её сечениях.

Таким образом, уравнение Бернулли выражает закон сохранения механической энергии движущейся жидкости, которая может иметь три формы: энергия положения, энергия давления, кинетическая энергия. С геометрической точки зрения уравнение Бернулли может быть сформулировано так: для элементарной струйки идеальной жидкости сумма трёх высот — геометрической, пьезометрической, скоростной — есть величина постоянная вдоль струйки. При этом члены уравнения Бернулли имеют следующий физический смысл:

z, м - расстояние от произвольной выбранной горизонтальной плоскости сравнения до центра тяжести рассматриваемого сечения;

, м - пьезометрическая высота такого столба жидкости, который у своего основания создает давление р, Па, равное давлению в рассматриваемом сечении элементарной струи;

- высота, с которой должно упасть в пустоте тело, чтобы приобрести скорость u м/с, на рисунке 1.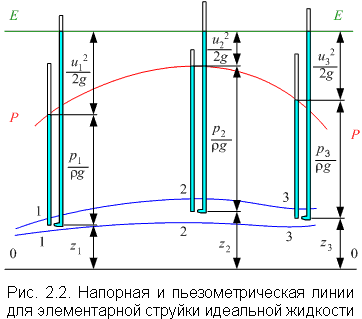


Рисунок 1 – Напорная и пьезометрическая линии для элементарной струйки идеальной жидкости

При геометрической интерпретации уравнения Бернулли вводится понятие пьезометрической и напорной линии. Линия, соединяющие сумму отрезков ( 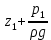) называется пьезометрической линией. Линия, соединяющая сумму отрезков ( 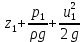) называется напорной линией (для идеальной жидкости это горизонтальная линия Е-Е).

С энергетической точки зрения уравнение Бернулли выражает закон сохранения энергии. Полный напор Н— это полная удельная механическая энермя жидкости в рассматриваемом сечении. Сумма трех членов есть сумма трех удельных энергий: удельной потенциальной энергии давления , удельной потенциальной энергии положения z, удельной кинетической энергии и

---

. Для идеальной жидкости сумма трех удельных энергий (полный напор) по длине струйки есть величина постоянная.

Если вместо идеальной жидкости рассматривать жидкость реальную (в отличие от идеальной, обладает вязкостью), рисунок 2, в которой при движении происходят потери на сопротивление, то уравнения Бернулли для двух сечений элементарной струйки реальной жидкости примет вид:

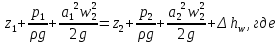
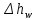– потеря напора между рассматриваемыми сечениями струйки 1 и 2 (линия Е-Е), включающая потери на трение 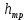, и потери на местных сопротивлениях ;

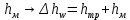a – коэффициент Кориолиса;

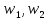– средние значения скорости потока, м/с.

Коэффициент Кориолиса представляет собой отношение действительной кинетической энергии потока в данном сечении к величине кинетической энергии, вычисленной по средней скорости, и зависит от степени неравномерности распределения скоростей в поперечном сечении потока. Для ламинарного режима а=2, а для турбулентного режима a 1,1.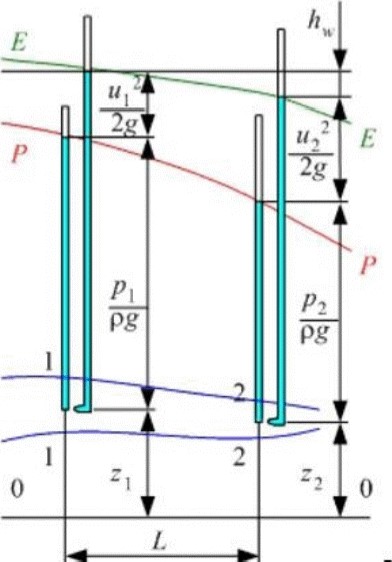


Рисунок 2 – Напорная и пьезометрическая линии для элементарной струи реальной жидкости
Уравнение Бернулли может быть изображено графически. Для этого по оси абсцисс откладывают расстояния между сечениями трубопровода, а по оси ординат- значения составляющих напора для этих же сечений. Обычно, чтобы иметь полную характеристику трубопровода, строят пьезометрическую и напорную линии.

Схема лабораторного стенда приведена на рисунке 3.



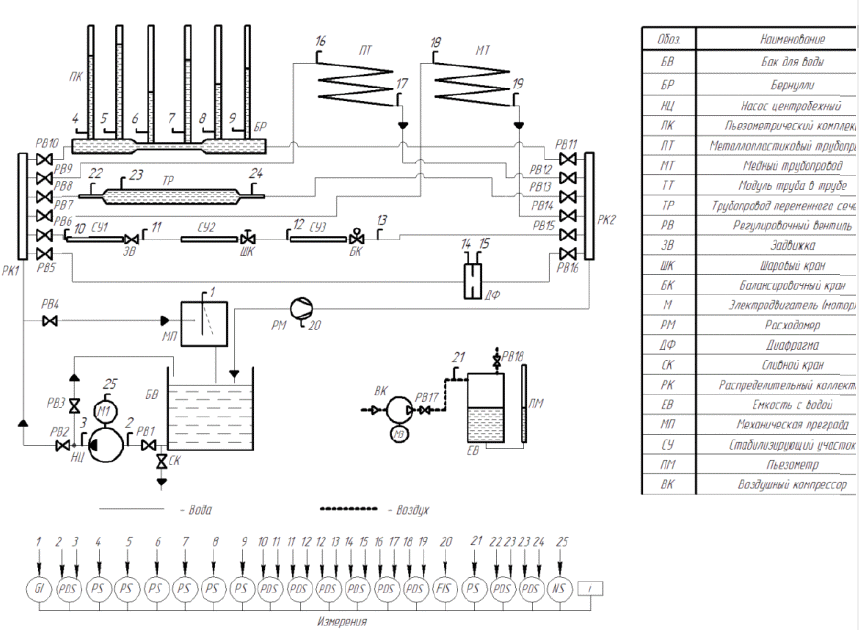
Рисунок 3 – Схема лабораторного стенда
Ход работы

1. 
   Сняты уровня воды в пьезометрических трубках (в основном выше середины)
   
2. 
   Выполнены необходимые расчеты для построения диаграммы уравнения Бернулли в таблице 1.
   

№ сечения	d, мм	f,	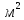V,	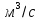w, м/с	, м	, м	H, м	????h, м
1-1	30	0,0007	0,00009	0,129	0,3	0,007	0,307	–
2-2	10	0,00008	0,00009	1,125	0,218	0,057	0,275	0,084
3-3	30	0,0007	0,00009	0,129	0,25	0,007	0,257	0,018

---

Для сечения 1-1:

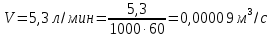
Рассчитана средняя скорость движения жидкости в трубе:




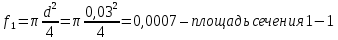
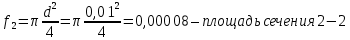
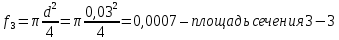
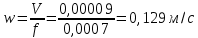
Скоростной напор:

Полная удельная энергия в сечении с показания пьезометров:

Показания пьезометров приведены на рисунке 4





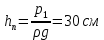
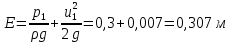
Рисунок 4 – Показания пьезометров


=0,218

=0

=0,007

=0,057

=0,007


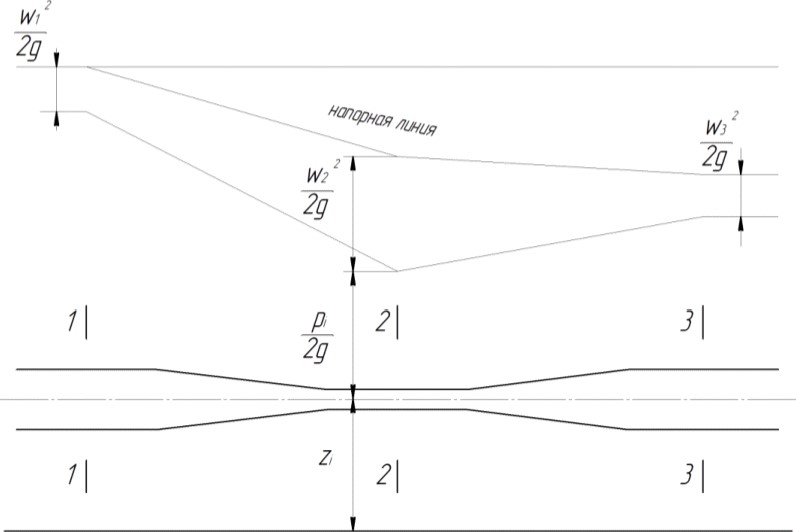
Рисунок 5 – Иллюстрация уравнения Бернулли
Вывод: после выполнения данной лабораторной работы были получены умения по нахождению уравнения Бернулли.

По результатам расчетов видно, что на сечении 2-2 наибольшая величина потери напора из-за наименьшей площади сечения трубопровода.

---

Смотрите также файлы

• "Менеджмент качества производства".pptx

• "Менеджмент качества производства".ppt

• Этап урока Метод и приемы Хронометраж.doc

• азіргі заманы дниежзіні геосаяси кеістігі.pptx

• Практическая работа 1 2 Тестирование программ методами белого ящика Цель работы.docx