Добавлен: 19.03.2024
Просмотров: 9
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вариант 16
Задача 1
Ф
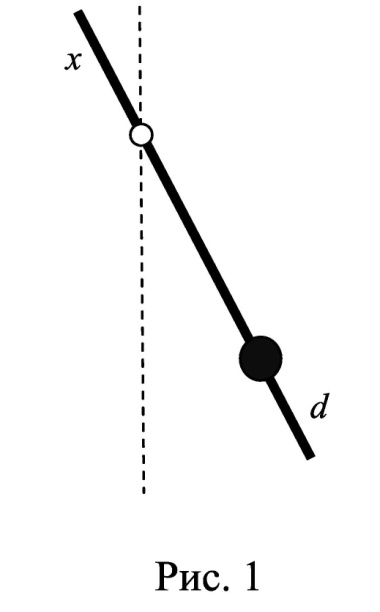 изический маятник представляет собой тонкий однородный стержень длиной
изический маятник представляет собой тонкий однородный стержень длиной 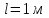 и массой m, на котором жестко закреплена материальная точка массой Mна расстоянии d
и массой m, на котором жестко закреплена материальная точка массой Mна расстоянии d 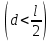 от нижнего конца стержня. Точка подвеса маятника находится на расстоянии x
от нижнего конца стержня. Точка подвеса маятника находится на расстоянии x 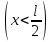 от верхнего конца стержня (рис. 1). Найти зависимость периода малых колебаний T маятника от расстояния xи построить график этой зависимости T(x) в интервале изменения xот 0 до l/2. Определить по графику минимальное значение периода T колебаний маятника. Ускорение свободного падения
от верхнего конца стержня (рис. 1). Найти зависимость периода малых колебаний T маятника от расстояния xи построить график этой зависимости T(x) в интервале изменения xот 0 до l/2. Определить по графику минимальное значение периода T колебаний маятника. Ускорение свободного падения 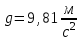 .
.| Дано: 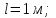 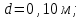 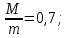 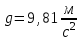 . . | Решение: Рассмотрим рисунок 2. Зададим систему отсчёта. За начало отсчёта принимаем верхний конец стержня, ось x направляем вертикально вниз. Координата центра масс физического маятника вычисляется по формуле: 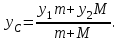 (1) (1)Г 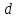 де де 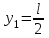 - координата центра стержня, - координата центра стержня,  - координата материальной точки массой М, - координата материальной точки массой М, 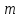 - масса стержня. - масса стержня.После подстановки соответственных выражений в формулу (1), получаем: 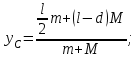 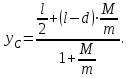 (2) (2)Тогда расстояние от центра масс к оси вращения маятника будет: 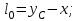 | ||||||||||||||
| Найти: 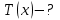 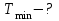 | |||||||||||||||
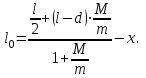 (3) (3)Подставим известные значения физических величин в расчётную формулу (3) и произведём вычисления: 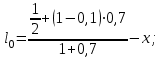 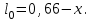 (4) (4)Период колебаний физического маятника вычисляется по формуле: 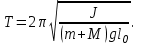 (5) (5)Где 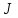 - момент инерции физического маятника относительно заданной оси вращения. - момент инерции физического маятника относительно заданной оси вращения.Момент инерции физического маятника вычисляется по формуле: 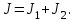 (6) (6)Где 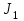 - момент инерции стержня относительно заданной оси вращения, - момент инерции стержня относительно заданной оси вращения, 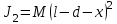 - момент инерции материальной точки относительно оси вращения. - момент инерции материальной точки относительно оси вращения.Момент инерции стержня относительно оси которая проходит через верхний конец стержня перпендикулярно ему вычисляется по формуле: 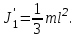 (7) (7)По теореме Штейнера найдём момент инерции стержня относительно заданной оси вращения: 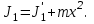 (8) (8)Подставляя (7) в формулу (8), имеем: 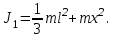 (9) (9)После подстановки в формулу (6) соответственных выражений, получаем: 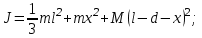 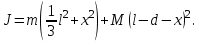 (10) (10)Подставляя (4) и (10) в формулу (5), имеем: 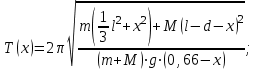 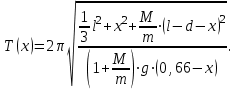 (11) (11)Подставим известные значения физических величин в расчётную формулу (11) и произведём вычисления: 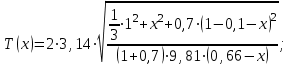 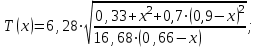 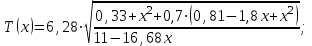 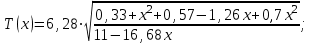 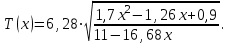 (12) (12)Для построения графика зависимости 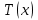 составим таблицу используя программу Еxcel: составим таблицу используя программу Еxcel:
Строим график зависимости 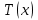 : : По графику зависимости 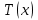 находим минимальное значение периода колебаний физического маятника. находим минимальное значение периода колебаний физического маятника.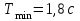 . .Ответ: 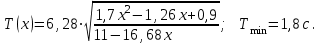 | |||||||||||||||
Задача 2
Материальная точка совершает одновременно гармонические колебания в двух взаимно перпендикулярных направлениях: вдоль оси x - по закону
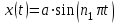 , вдоль оси y - по закону
, вдоль оси y - по закону 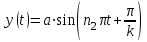 ,
, 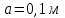 Построить траекторию движения материальной точки.
Построить траекторию движения материальной точки.| Дано: 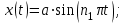 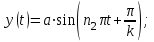 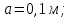 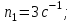 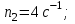 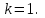 | Решение: Подставим численные значения физических величин в заданные законы колебаний материальной точки: 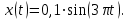 (1) (1)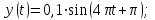 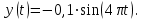 (3) (3)С формулы (1) выражаем время: 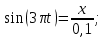 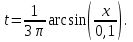 (4) (4)После подстановки (4) в формулу (3), получаем: 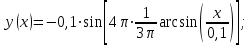 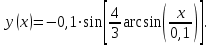 (5) (5)Для построения графика зависимости 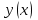 составим таблицу используя программу Еxcel: составим таблицу используя программу Еxcel:
Строим график зависимости 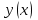 : : | ||||||||||||||||||||||||||
| Найти: 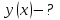 | |||||||||||||||||||||||||||
 Ответ: 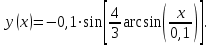 | |||||||||||||||||||||||||||
З
 адача 3
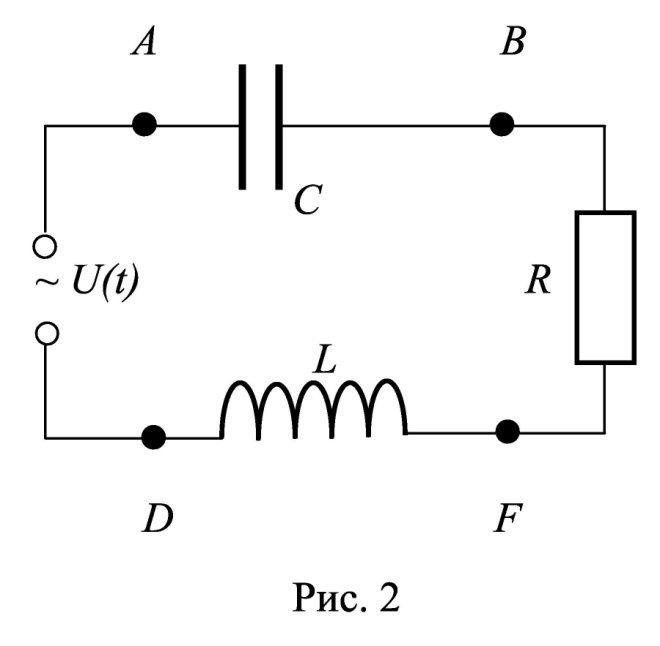
адача 3 Сила тока в электрическом контуре (рис. 2) меняется со временем по закону:
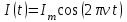 ,
, 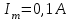 ,
, 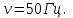 Найти амплитуду напряжения и сдвиг фаз между током и напряжением на заданном участке цепи BD.
Найти амплитуду напряжения и сдвиг фаз между током и напряжением на заданном участке цепи BD.Построить график зависимости напряжения U(t) на этом участке от времени t в интервале изменения tот 0 до 40мс.
| Дано: 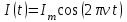 ; ;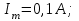 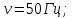 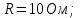 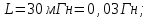 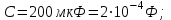 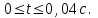 | Решение: Найдём общее сопротивление заданного участка цепиBD по формуле: 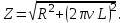 (1) (1)Подставим численные значения физических величин в формулу (1) и произведём вычисления: 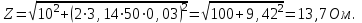 Сдвиг фаз между током и напряжением на заданном участке цепи BD, вычисляется по формуле: 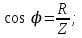 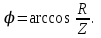 (2) (2)Подставим численные значения физических величин в формулу (2) и произведём вычисления: 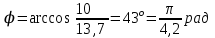 . .По закону Ома для участка цепи, получаем: 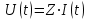 . (3) . (3)Учитывая условие задачи, имеем 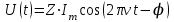 . (4) . (4)Подставим известные значения физических величин в формулу (2) и произведём вычисления: | ||||||||||||||||||||
| Найти: 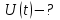 | |||||||||||||||||||||
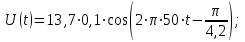 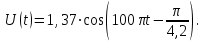 (5) (5)Для построения графика зависимости  составим таблицу используя программу Еxcel: составим таблицу используя программу Еxcel:
 Строим график зависимости 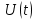 : :Ответ: 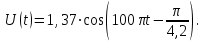 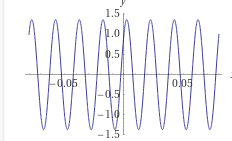 | |||||||||||||||||||||
