Московский авиационный институт
(национальный исследовательский университет)

Кафедра 906.

КУРСОВАЯ РАБОТА
по курсу:
«Теория надёжности машин и
конструкций»

Вариант №12

Студент группы 9О-406Б

Ширяев А.С.

Преподаватель

Сидоренко А.С.

Москва. 2017

Прочность конструкции характеризуется одним прочностным случайным параметром R, а нагрузка – одним случайным параметром S.

ν= <R>/<S>.- условный коэффициент запаса прочности ν как отношение математических ожиданий параметров прочности и нагрузки

σ_R, σ_S – средние квадратические отклонения (СКО) величин R и S.

<R>_i = <S> ν_i , где <R>_i <S> математические ожидания

<Ψ> = <R> - <S> - случайная величина

γ= (ν-1)/(ν² w_R² + w_S²)^0,5 мера надёжности, где

w_R = σ_R /<R>, w_S = σ_S /<S> ‑ коэффициенты вариации прочности и нагрузки соответственно.
γ – квантиль нормального распределения является величиной, обратной коэффициенту вариации w_Ψ параметра Ψ, и называется гауссовой мерой надежности.


Тогда для значений <S> = 52 Мпа, σ_R = 5 Мпа, σ_S = 1.1 Мпа

i	1	2	3	4	5	6	7	8	9	10
νi	1,1	1,2	1,3	1,4	1,5	1,6	1,7	1,8	1,9	2,0
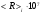	5.72	6.24	6.76	7.28	7.8	8.32	8.84	9.36	9.88	10.4
<Ψ>i	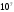0.52	1.04	1.56	2.08	2.6	3.12	3.64	4.16	4.68	5.2
γi	1.02	2.03	3.05	4.06	5.08	6.09	7.11	8.13	9.14	10.16
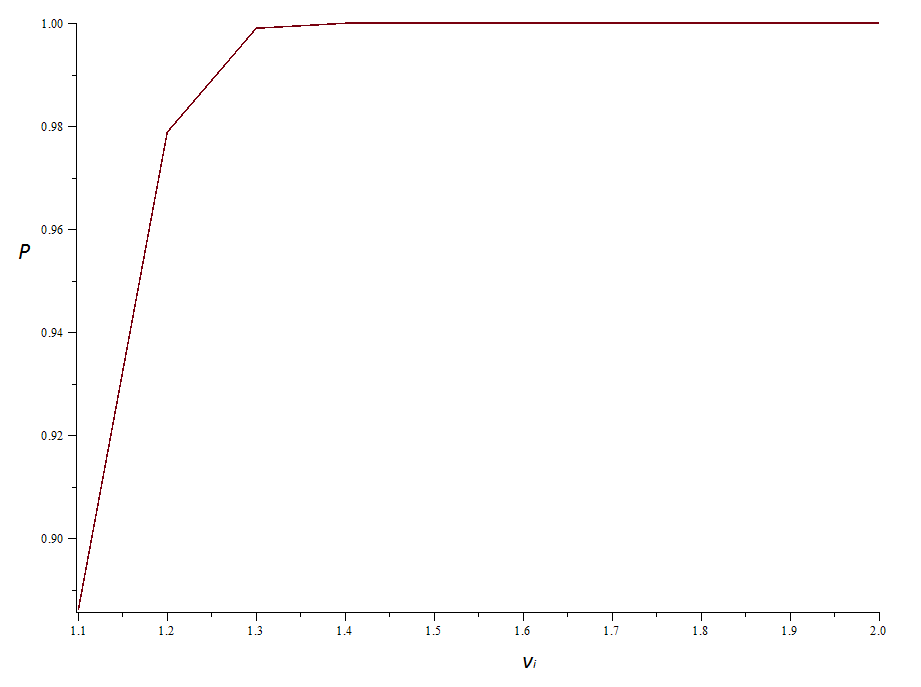
Pi	0.8861	0.9788	0.9989	1	1	1	1	1	1	1

---

---

Смотрите также файлы

• Был трудный бой. Всё нынче, как спросонку, и только не могу себе простить.docx

• Екатерина Первая Императрица России.pptx

• Что такое cmmi Capability Maturity Model Integration (cmmi) Комплексная модель производительности и зрелости набор моделей (методологий) совершенствования процессов в организациях разных размеров и видов деятельности..docx

• Конспект Под реализацией понимается передача товаров с переходом права собственности, хозяйственного ведения, оперативного управления передача результатов выполненных работ оказание услуг другому лицу.doc

• Древнерусское государство (Киевская Русь) Древнерусское государство.docx