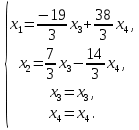ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.03.2024
Просмотров: 11
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования
«Тольяттинский государственный университет»
| (наименование института полностью) |
| |
| (Наименование учебного структурного подразделения) |
| 13.03.02 Электроэнергетика и электротехника |
| (код и наименование направления подготовки / специальности) |
| Электроснабжения |
| (направленность (профиль) / специализация) |
Практическое задание №_1__
по учебному курсу Высшая математика.Элементы высшей алгебры и геометрии »
(наименование учебного курса)
Вариант 13,6,3 (при наличии)
| Обучающегося | Е.В.Ямилев | |
| | (И.О. Фамилия) | |
| Группа | ЭЭТбп-2201а | |
| | | |
| Преподаватель | С.А.Крылова | |
| | (И.О. Фамилия) | |
Тольятти 2022_
РАЗДЕЛ № 1. ЛИНЕЙНАЯ АЛГЕБРА
Задача 1. Определить собственные значения и собственные векторы матрицы третьего порядка.
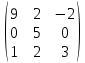
Решение.
1) Найдем собственные числа из характеристического уравнения:
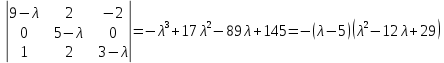
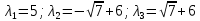
2) Для каждого
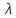найдем его собственные вектора: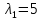
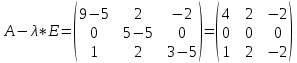
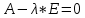
Тогда имеем однородную систему линейных уравнений, решим ее методом Гаусса:
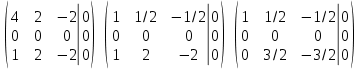
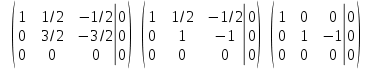
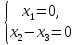
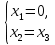
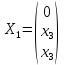
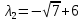
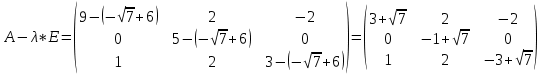
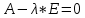
Тогда имеем однородную систему линейных уравнений, решим ее методом Гаусса:
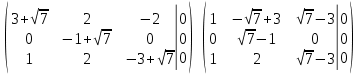
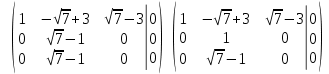
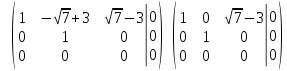
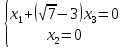
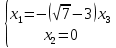
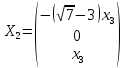
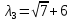
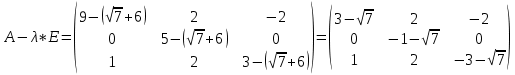
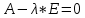
Тогда имеем однородную систему линейных уравнений, решим ее методом Гаусса:
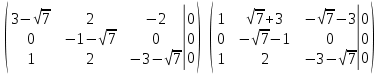
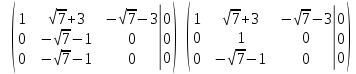
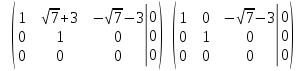
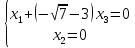
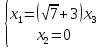
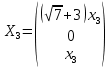
Задача 2. Доказать совместность системы и решить её тремя способами: по формулам Крамера, методом Гаусса и средствами матричного исчисления.
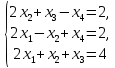
Решение.
Исследуем систему на совместность. Воспользуемся теоремой Кронекера-Капелли, для этого найдем ранг расширенной матрицы системы и ранг матрицы системы. Найдем ранг матрицы методом элементарных преобразований. Ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы.
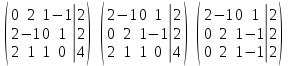
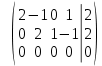
Ранг расширенной матрицы равен рангу матрицы системы, но меньше числа неизвестных. Система совместна и имеет бесконечно много решений.
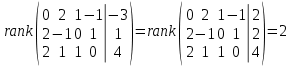
Данную систему можно решить только методом Гаусса:
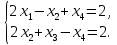
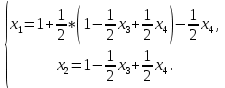
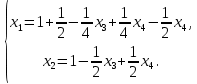
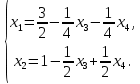
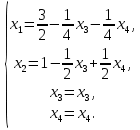
Задача 3. Исследовать и найти общее решение системы линейных однородных уравнений.
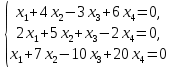
Решение.
Приведем расширенную матрицу системы к ступенчатому виду:
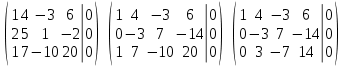
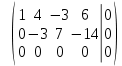
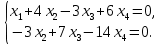
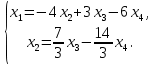
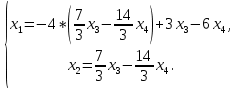
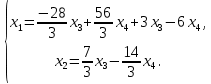
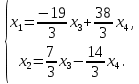
Общее решение имеет вид:
