ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.03.2024
Просмотров: 12
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вывод. В рассматриваемой совокупности половина значение признак не менее 127,5 единиц, а другая половина – не более 127,5 единиц.
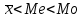 , следовательно, асимметрия левосторонняя. В совокупности преобладают единицы с более высокими значениями признака, чем среднее значение.
, следовательно, асимметрия левосторонняя. В совокупности преобладают единицы с более высокими значениями признака, чем среднее значение.Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине Q1; 25% будут заключены между Q1и Q2; 25% - между Q2и Q3; остальные 25% превосходят Q3.
0-й квартиль – минимальное значение признака;
2-й квартиль – медиана;
1-й и 3-й квартиль рассчитываются аналогично медиане.
Значение Q1 будет там находиться в интервале 700-100, т.к. именно в этом интервале накопленная частота 16 впервые превышает четверть суммы частот
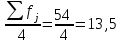 .
.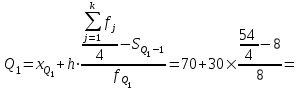 120,63
120,63Значение Q3 будет там находиться в интервале 130-160, т.к. именно в этом интервале накопленная частота 42 впервые превышает три четверти суммы частот
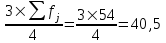 .
.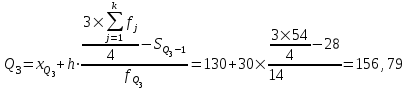
Децили делят совокупность на 10 равных частей. Рассчитываются аналогично медиане и квартилям.
Интервалом 1-го дециля d1 будет является интервал 40-70 (до 70), т.к. именно в этом интервале накопленная частота 8 впервые превышает 1/10 суммы частот
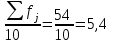 .
.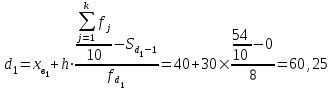
Интервалом 9-го дециля d9 будет интервал 190-220 т.к. в этом интервале накопленная частота 52 впервые превышает 9/10 суммы частот
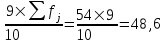 .
.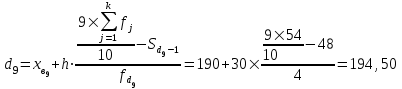
10. Вычислим показатели вариации
Размах вариации характеризует амплитуду колебаний значений признака, рассчитывается как разность максимального и минимального значения признака. По исходным данным (таблица 1) размах вариации:
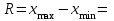 241 – 47 = 194
241 – 47 = 194Среднее линейное отклонение:
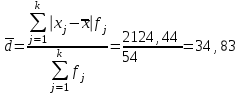
Дисперсия:
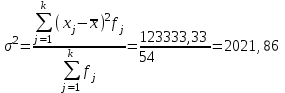
Среднее квадратическое отклонение:
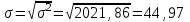
Вывод. Отклонение от среднего значения признака в ту или иную сторону составляет 44,97 единиц.
Коэффициент вариации является мерой относительной колеблемости признака около средней и характеризует степень однородности признака в изучаемой совокупности:
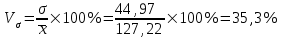
Вывод. Значение коэффициента вариации не превышает 40%, следовательно, вариация признака в исследуемой совокупности единиц незначительная. Однако значение коэффициента вариации больше 33,3%. это говорит о том, что совокупность не однородна. Найденное среднее значение не является типичной и надежной характеристикой среднего.
Относительное линейное отклонение
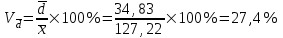
Коэффициент осцилляции:
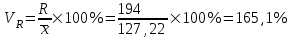
Вывод. Доля среднего линейного отклонения в среднем значении признака составляет 27,4%. Доля размаха вариации в среднем значении – 165,1%.
11. Рассчитаем показатели асимметрии и эксцесса
Установлена следующая оценочная шкала асимметричности для коэффициента асимметрии Пирсона:
|As|
 0,25 - асимметрия незначительная;
0,25 - асимметрия незначительная;0,25<|As|
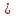 0,5 - асимметрия заметная (умеренная);
0,5 - асимметрия заметная (умеренная);|As|>0,5 - асимметрия существенная.
Расчет коэффициента асимметрии Пирсона:
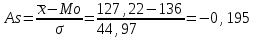
Вывод. Значения коэффициента асимметрии Пирсона отрицательное, что означает незначительную левостороннюю асимметрию распределения. Это означает, что в совокупности преобладают значения признака, более чем среднее.
Расчет коэффициента асимметрии:
Расчет коэффициента эксцесса:
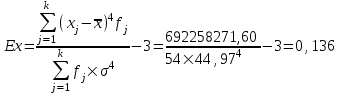
Вывод. Показатель эксцесса положительный, т.е. вершина кривой распределения лежит выше вершины кривой нормального закона распределения, а форма кривой более островершинная по сравнению с кривой нормального закона. Это означает, что значения признака концентрируются в центральной части ряда, а не рассеяны по всему диапазону.
Список использованных источников
-
Гусаров В.М. «Статистика». Учебное пособие для вызов. – М.: ЮНИ-ТИ-ДАНА, 2008, 463 с. -
Денисенко Р.М., Метелёв И.С. Статистика предприятия торговли: Учебное пособие. – Омск: Издатель Васильев В.В., 2007. - 108 с. -
Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник. – М.: ИНФРА – М, 2009. – 416 с. -
Рудакова Р.П., Букин Л.Л., Гаврилов В.И. Статистика. 2-е изд. – сПб.: Питер, 2007. – 288 с.: ил. -
Статистика: Учебное пособие / И.Е. Теслюк В.А. Тарловская, И.Н. Терлиженко и др., 2-е изд. – Мн: Ураджай, 2007 – 360 с., ил. -
Теория статистики: Учебник / Под ред. проф. Г.Л. Громыко. – 2-е изд., перераб. и доп. – М.: ИНФРА-М, 2006 – 476 с. -
Теория статистики: Учебник / Р.А.Шамойлова, В.Г.Минашкин, Н.А.Садовникова, Е.Б.Шувалова; Под ред. Р.А.Шамойловой. – 4-е изд., перераб. и доп. – М.: Финансы и статистика, 2006. – 656.

