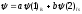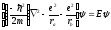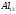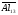ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.03.2024
Просмотров: 44
Скачиваний: 0
где
r — расстояние между электроном и ядром,
а р — радиус первой боровской орбиты.
Эта функция находится решением уравнения
Шредингера для случая электростатического
потенциала взаимодействия с ядром,
заданным как е/r. Уравнение для атома
водорода — одна из немногих точно
решаемых задач в физике, а сам он — одна
из наиболее глубоко понятых систем во
Вселенной. В случае молекулы, например,
иона теория молекулярных орбиталей
предполагает, что волновая функция
системы может быть описана как линейная
комбинация волновых функций
изолированных атомов. Таким образом,
волновая функция основного состояния
электрона в ионе
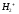 будет записана в виде
будет записана в виде
|
|
(2) |
Уравнение Шредингера для молекулярного иона имеет вид
|
|
(3) |
Символ
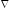 2
обозначает операцию двукратного
дифференцирования по координатам.
Два последних члена в квадратных скобках
описывают электростатическое притяжение
электрона к двум положительно заряженным
ядрам, находящимся на расстоянии ra
и rb
от электрона. Для молекулы водорода, в
которой присутствуют два электрона,
надо добавить член, ответственный за
электростатическое отталкивание между
ними. Уравнение Шредингера решено для
такой линейной комбинации волновых
функций (формула 2). Когда молекула
состоит из многих атомов и содержит
много электронов, задача становится
весьма сложной, и для ее решения применяют
множество приближенных методов. Теория
функционалов плотности является
одним из таких подходов. Увеличение
вычислительных мощностей компьютеров
и разработка новых теоретических
подходов сделали возможным определение
геометрической и электронной структуры
больших молекул методами теории
молекулярных орбиталей с высокой
точностью. Структуру с наименьшей
энергией можно найти вычислительными
методами, что и определяет равновесную
геометрию молекулы. Такие методы
молекулярных орбиталей с некоторыми
изменениями применимы и к металлическим
наночастицам.
2
обозначает операцию двукратного
дифференцирования по координатам.
Два последних члена в квадратных скобках
описывают электростатическое притяжение
электрона к двум положительно заряженным
ядрам, находящимся на расстоянии ra
и rb
от электрона. Для молекулы водорода, в
которой присутствуют два электрона,
надо добавить член, ответственный за
электростатическое отталкивание между
ними. Уравнение Шредингера решено для
такой линейной комбинации волновых
функций (формула 2). Когда молекула
состоит из многих атомов и содержит
много электронов, задача становится
весьма сложной, и для ее решения применяют
множество приближенных методов. Теория
функционалов плотности является
одним из таких подходов. Увеличение
вычислительных мощностей компьютеров
и разработка новых теоретических
подходов сделали возможным определение
геометрической и электронной структуры
больших молекул методами теории
молекулярных орбиталей с высокой
точностью. Структуру с наименьшей
энергией можно найти вычислительными
методами, что и определяет равновесную
геометрию молекулы. Такие методы
молекулярных орбиталей с некоторыми
изменениями применимы и к металлическим
наночастицам.
2.3 Геометрическая структура
Обычно кристаллическая структура наночастицы такая же, как и у объемного материала, но с несколько отличающимся параметром решетки. Рентгеновская дифракция для частицы алюминия размером 80 нм показывает элементарную ячейку
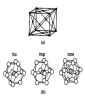
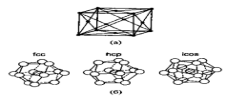
Рисунок 6 – (а) — Элементарная ячейка объемного алюминия, (б) — Три возможных структуры кластера А113: ГЦК, ГПУ и икосаэдрическая.
ГЦК-решетка, изображенную на рис. 6(а), такую же, как и у объемного алюминия. Однако в некоторых случаях малые частицы с размерами < 5 нм могут иметь другую структуру. Например, показано, что частицы золота размерами 3-5 нм имеют икосаэдрическую структуру, хотя в объеме золото кристаллизуется в ГЦК-решетку. Интересно рассмотреть алюминиевый кластер из 13 атомов, так как это - магическое число.
На рис. 6(б) показаны три возможных расположения атомов в кластере. На основе критерия максимизации количества связей при минимизации объема, а также того факта, что в объеме структурой алюминия является ГЦК, можно ожидать, что структура такой наночастицы также будет ГЦК. Однако вычисления молекулярных орбиталей по методу функционалов плотности предсказывают, что наименьшую энергию имеет икосаэдрическая форма, то есть вероятно изменение структуры. Пока не существует экспериментальных данных о структуре Аl13 частицы, подтверждающих такое предположение. Экспериментальное определение структуры малых металлических наночастиц весьма сложно, так что количество таких данных невелико. В конце 70-х и начале 80-х годов Г.Д. Штейн смог определить структуры наночастиц BiN, PbN, InN и AgN. Частицы создавались путем испарения металла в печи, а в результате последующего выноса частиц потоком инертного газа и его сверхзвукового расширения инициировалось образование кластеров. Для кластеров менее 8 нм в диаметре наблюдались отклонения от ГЦК-структуры. Индиевые кластеры претерпевают структурные изменения при уменьшении размеров ниже 5,5 нм. Выше 6,5 нм, что соответствует примерно 6000 атомов, кластер имеет тетрагональную ГЦК-структуру с отношением с/а, равным 1,075. В тетрагональной элементарной ячейке все ребра перпендикулярны друг другу, длинная ось обозначается как с, две коротких как а. Ниже 6,5 нм отношение с/а уменьшается и при 5 нм достигает единицы, то есть структура становится кубической.
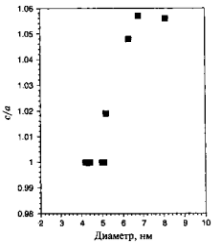
Рисунок 7 – Отношение длин осей с/а в тетрагональной элементарной ячейке наночастицы иридия в зависимости от диаметра наночастицы.
На рис. 7 показана зависимость с/а от диаметра частицы индия. Следует отметить, что структура изолированной наночастицы может отличаться от лиганд-стабилизированной структуры. Лиганд-стабилизацией называется присоединение неметаллических ионных групп к металлическим атомам или ионам. Изменение структуры может отразиться на многих свойствах, в частности — на электронной структуре.
Таблица 1 – Вычисление энергии святи на один атом и межатомные расстояния для некоторых наночастиц алюминия в среднем со значениями для объемного образца.
|
Кластер |
Энергии связи (эВ) |
Расстояние (А) |
|
|
2,77 |
2,814 |
|
|
3,10 |
2,75 |
|
Объемный |
3,39 |
2,86 |
В Таблице 1 приведены результаты вычислений по методу функционалов плотности некоторых электронных свойств частицы Аl13. Заметим, что энергия связи, приходящаяся на один атом в Аl13, меньше, чем в объемном кристалле. У кластера Аl13 один электрон на внешней оболочке не спарен. Добавление электрона заполняет оболочку. Что приводит к заметному увеличению энергии связи в ионе Аl13(-). Метод молекулярных орбиталей способен также объяснить зависимость энергии связи и ионизационного потенциала от количества атомов в кластере. На рис. 8 показаны некоторые примеры структур наночастиц бора разных размеров, вычисленные таким способом.
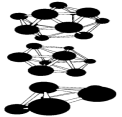
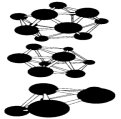
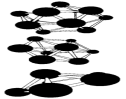
Рисунок 8 – Пример некоторых рассчитанных структур малых наночастиц бора.
Рис. 6 и 8 иллюстрируют и другое важное свойство наночастиц: для мелких кластеров все атомы, составляющие частицу, находятся на ее поверхности, что оказывает сильное влияние на многие их свойства: колебательные уровни, стабильность, реакционную способность.
Хотя металлические наночастицы рассматриваются как изолированные объекты, это не всегда имеет место в действительности. Некоторые наночастицы, такие как алюминий, имеют высокую реакционную способность. Если бы можно было поместить в воздухе изолированную наночастицу алюминия, она немедленно окислилась бы кислородом воздуха и покрылась слоем оксида Аl2O3. Рентгеновская фотоэлектронная спектроскопия 80-нанометровых частиц алюминия, пассивированных кислородом, показывает, что слой Аl2O3 на их поверхности составляет 3-5 нм. Наночастицы могут быть получены также и в жидких средах, что исключает контакт с воздухом. Например, наночастицы алюминия можно получить разложением гидрида алюминия в некоторых нагретых растворах. В таком случае с поверхностью наночастицы могут связываться молекулы растворителя, или может быть добавлено поверхностно активное вещество (ПАВ), такое как олеиновая кислота. ПАВ покрывает наночастицы и препятствует их агрегированию. Такие металлические частицы называют пассивированными, поскольку они покрыты слоем некоторого другого вещества. Химическая природа этого слоя оказывает существенное влияние на свойства наночастицы. Самособирающиеся монослои тоже могут быть использованы для покрытия наночастиц. Наночастицы золота можно пассивировать самособранным слоем, используя октадецилтиол (С18Н37S - Au). Здесь длинная углеводородная цепочка привязывается за один конец тиоловой группой БН к наночастице золота с образованием сильной связи S - Аu. Притяжение между молекулами приводит к их симметрично упорядоченному расположению вокруг частицы. Такое симметричное расположение молекул вокруг частицы характерно для самосборных монослоев.
2.4 Электронная структура
Когда
атомы формируют решетку, их дискретные
энергетические уровни расщепляются в
энергетические зоны. Термин плотность
состояний означает количество
энергетических уровней в заданном
интервале энергий. В металле верхняя
энергетическая зона заполнена не до
конца. В случае полупроводника верхняя
занятая зона, называемая валентной,
заполнена до конца и отделяется от
следующей, пустой зоны небольшим
промежутком, называемым щелью. Когда
частица металла уменьшается в размерах
до нескольких сотен атомов, плотность
состояний в зоне проводимости — верхней
зоне, содержащей электроны — радикально
меняется. Непрерывная плотность состояний
в зоне заменяется набором дискретных
уровней, интервалы между которыми могут
оказаться больше, чем тепловая энергия
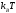 ,
что приводит к образованию щели. Изменения
электронной структуры при переходе от
объемного кристалла к большому кластеру,
а затем - к маленькому кластеру с размерами
меньше 15 атомов, показаны на рис. 9.
,
что приводит к образованию щели. Изменения
электронной структуры при переходе от
объемного кристалла к большому кластеру,
а затем - к маленькому кластеру с размерами
меньше 15 атомов, показаны на рис. 9.
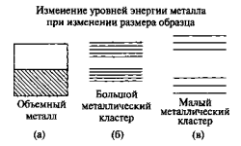
Рисунок 9 – Пример изменения уровней энергии металла при уменьшении количества атомов: (а) - валентная зона объемного металла; (б) — в большом кластере из 100 атомов возникает запрещенная зона; (в) — маленький кластер, состоящий из трех атомов.
Маленький кластер аналогичен молекуле с ее дискретным набором энергетических уровней, связывающими и антисвязывающими орбиталями. В конце концов, можно уменьшить кластер до размеров, при которых расстояние между противоположными гранями приблизится к длине волны электрона. В таком случае энергетические уровни могут быть получены путем рассмотрения квантовой задачи о частице в потенциальном ящике. Это называется квантовым размерным эффектом. Появление новых электронных свойств можно понять в терминах принципа неопределенности Гейзенберга, утверждающего, что чем лучше электрон локализован в пространстве, тем шире будет диапазон его импульса. Средняя энергия будет определяться не столько химической природой атомов, сколько размером частицы. Интересно отметить, что квантовый размерный эффект появляется в полупроводниках при больших размерах, чем в металлах, из-за большей длины волны электронов и дырок в полупроводниках. В полупроводниках длина волны может достигать микрона, в то время как в металлах она составляет порядка 0.5 нм.