Файл: Международный консорциум Электронный университет Московский государственный университет экономики, статистики и информатики.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.03.2024
Просмотров: 313
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
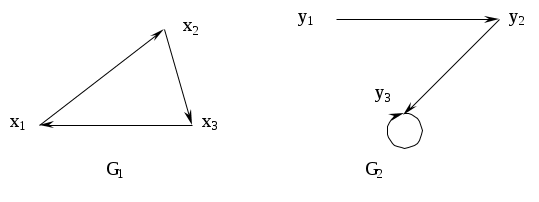
-
Найти декартово произведение графов, заданных с помощью матриц смежности
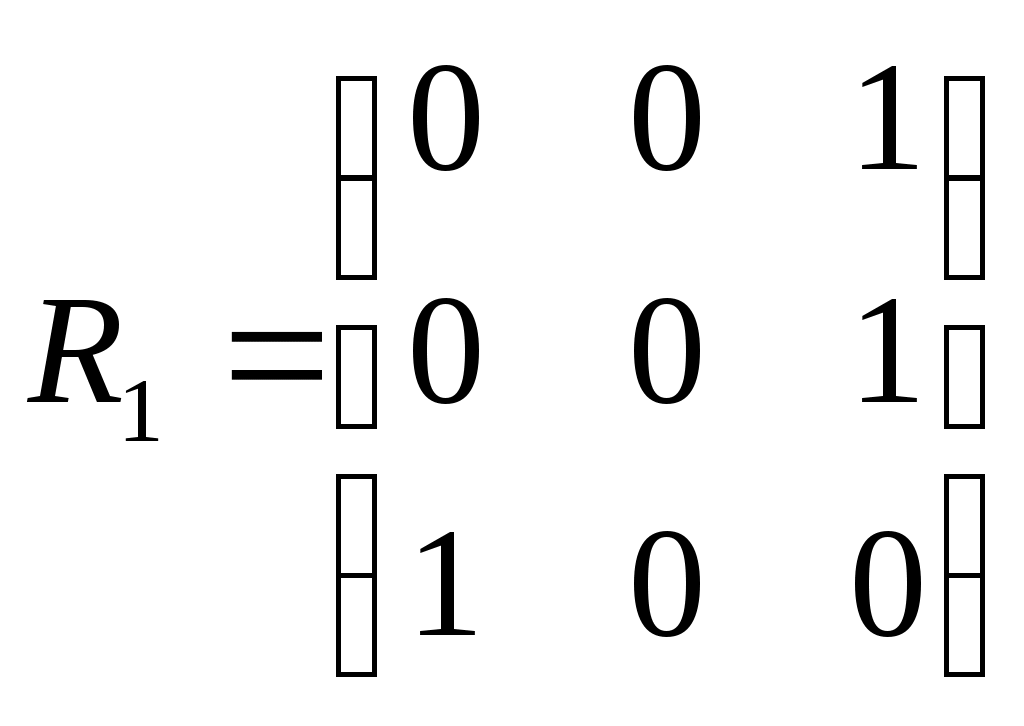 | 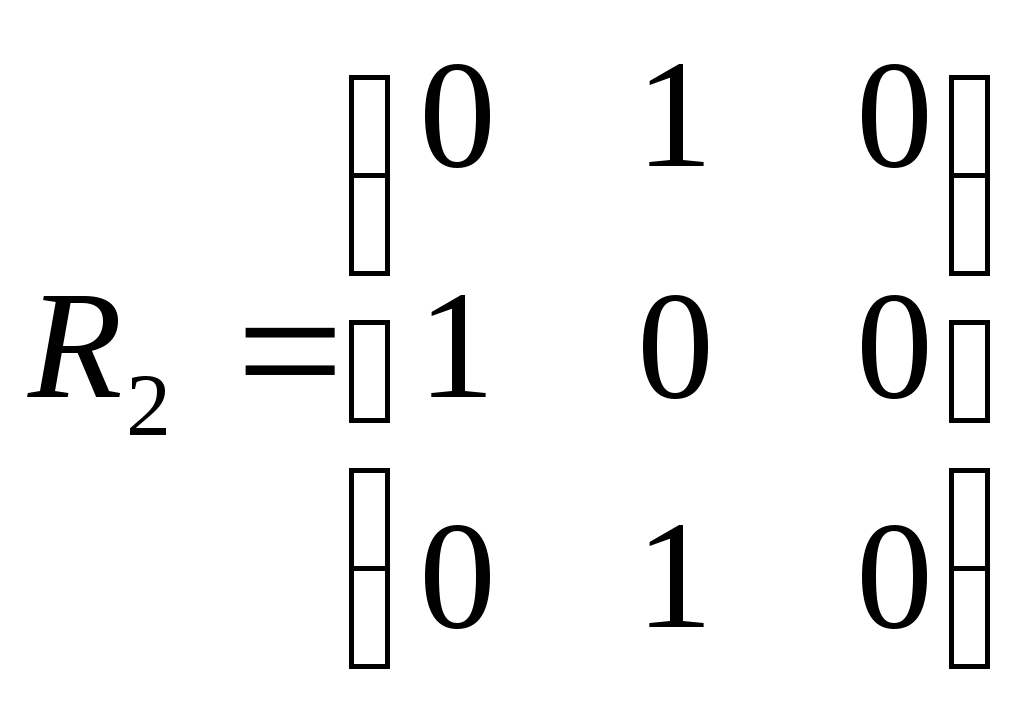 |
-
Даны матрицы инциденций двух графов. Найти их декартово произведение
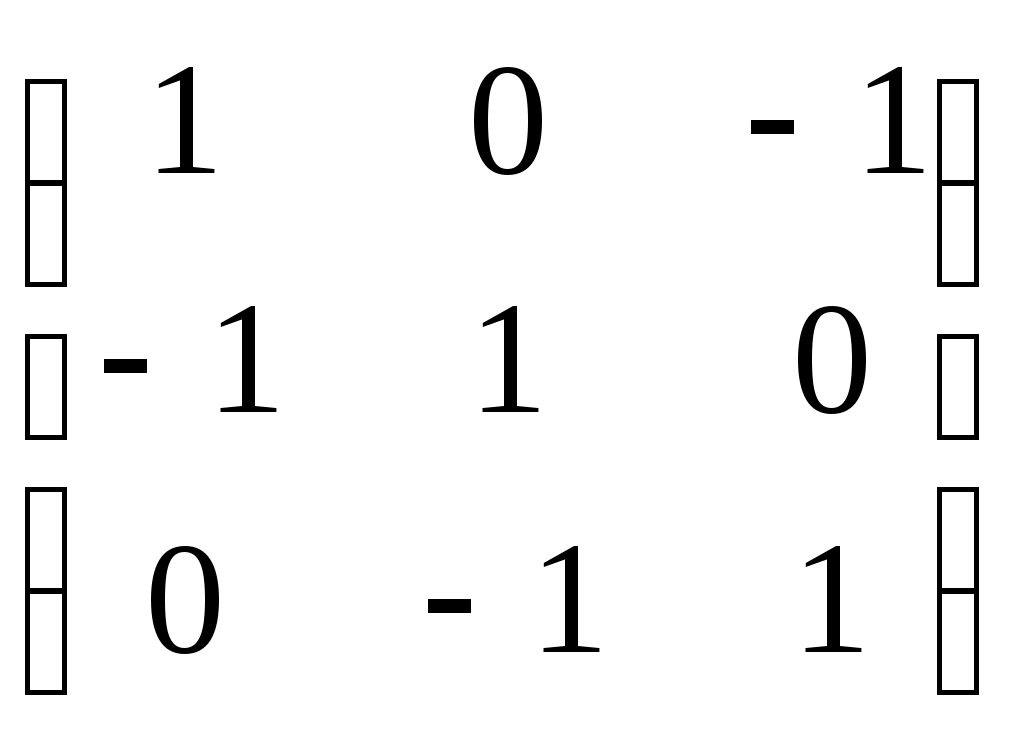 | 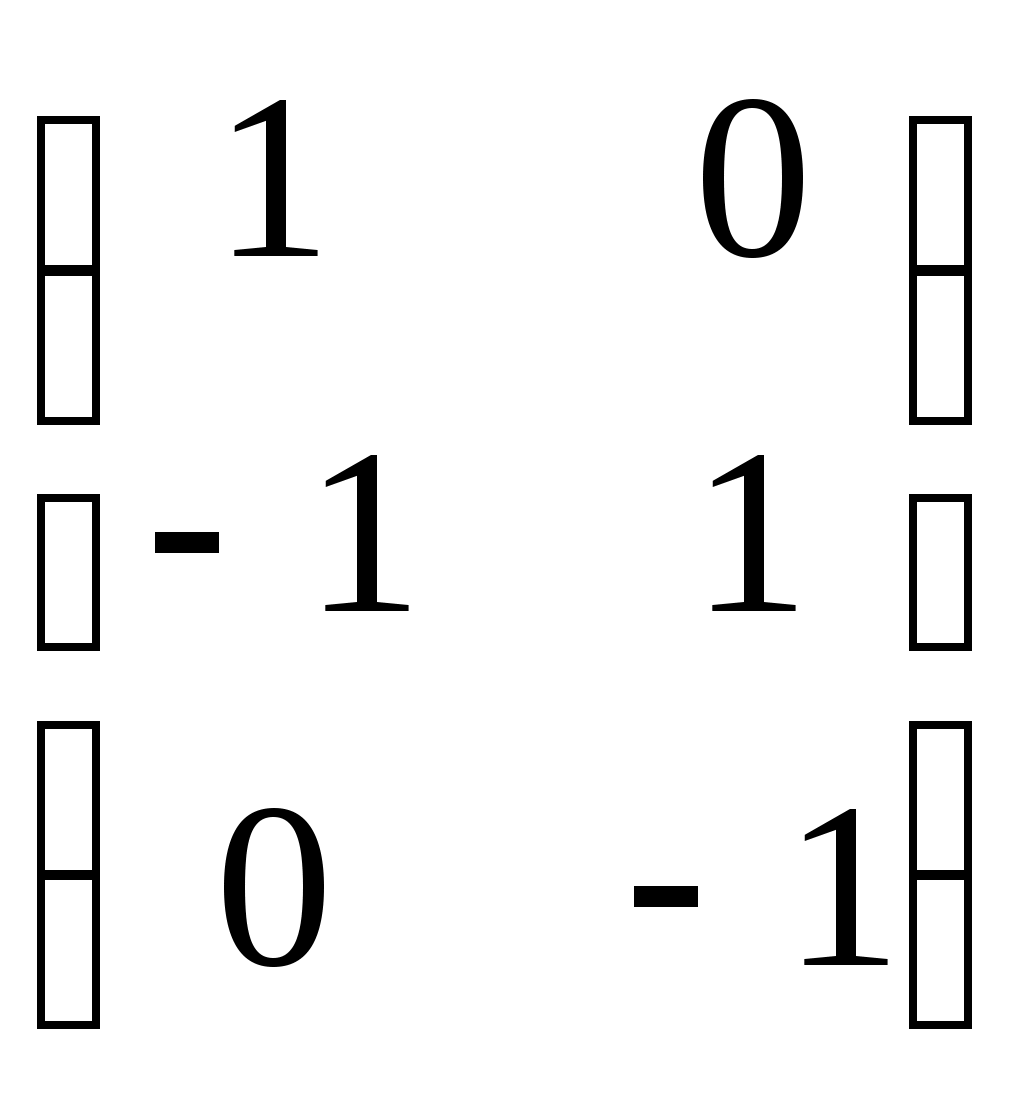 |
-
Найти декартово произведение двух графов.
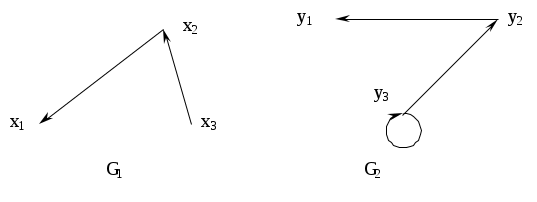
-
Найти декартово произведение двух графов.
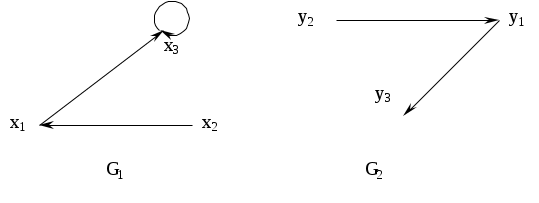
Контрольное задание №15
-
Строится нефтепровод, соединяющий города х1……x11. Стоимость возможных участков строительства задана таблицей.
| | х1 | х2 | х3 | х4 | х5 | х6 | х7 | х8 | х9 | х10 | х11 |
| х1 | 0 | 6 | | 10 | | | | | | | |
| х2 | | 0 | 6 | | 8 | 6 | | | | | |
| х3 | | | 0 | | | | 11 | | | | |
| х4 | | | | 0 | 3 | | | | | 5 | |
| х5 | | | | | 0 | 9 | | 4 | | | |
| х6 | | | | | | 0 | | | | | |
| х7 | | | | | | | 0 | | 12 | | |
| х8 | | | | | | | | 0 | | 7 | |
| х9 | | | | | | | | | 0 | 11 | 10 |
| х10 | | | | | | | | | | 0 | 9 |
| х11 | | | | | | | | | | | 0 |
Изобразить схему нефтепровода, стоимость строительства которого минимальна, и подсчитать минимальные затраты.
-
Каждый из шести городов может быть соединен с другим участком газопровода, стоимость строительства которого указана в таблице.
| | х1 | х2 | х3 | х4 | х5 | х6 |
| х1 | 0 | 2 | 4 | 9 | 6 | 10 |
| х2 | | 0 | 3 | 3 | 9 | 7 |
| х3 | | | 0 | 5 | 8 | 8 |
| х4 | | | | 0 | 7 | 10 |
| х5 | | | | | 0 | 11 |
| х6 | | | | | | 0 |
Как построить самый дешевый нефтепровод, какова стоимость его строительства?
-
10 городов, обозначенных на графе вершинами х1…x10, необходимо соединить электролинией. Возможные соединения обозначены ребрами. Стоимость строительства на участке (хi,xj) обозначена соответствующим числом.
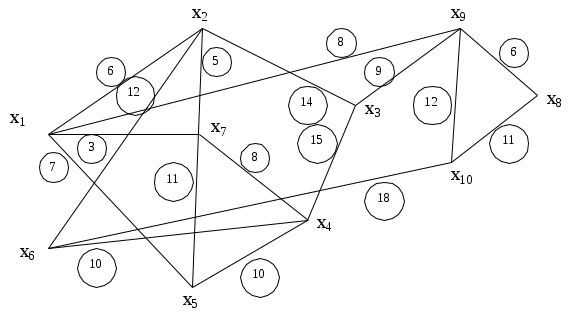
Определить стоимость строительства самой дешевой электролинии. Как она должна проходить?
-
На строительство электролинии между городами х1…..х7 отпущено 250 тысяч рублей. Стоимость строительства на возможных участках между городами хi,хj l(хi хj) в тыс. руб. задана следующим образом:
| l(x1,x2)=40 l(x1,x3)=50 l(x1,x6)=60 l(x1,x7)=50 l(x2,x3)=30 | l(x2,x6)=20 l(x2,x7)=30 l(x2,x4)=90 l(x3,x4)=60 l(x3,x7)=60 | l(x4,x5)=90 l(x4,x7)=70 l(x5,x6)=80 l(x5,x7)=100 l(x6,x7)=10 |
Как построить электролинию, чтобы уложиться в эту смету?
-
Определить наименьшие затраты при перевозке груза из пункта х0 в пункт х6 через перевалочные пункты х1,х2,х3,х4,х5. Стоимость перевозки груза из пункта хi в хj указана на графе. Определить путь, соответствующий минимальной стоимости.
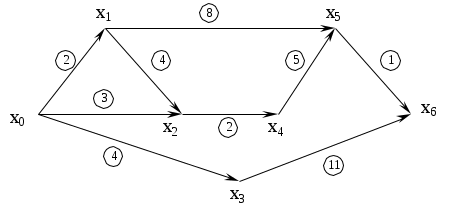
-
Из пункта А в пункт N перевозят однородный груз, используя перевалочные пункты В, С, D, Е, F, G. Расстояние между пунктами, соединенными дорогами, указаны на графе.
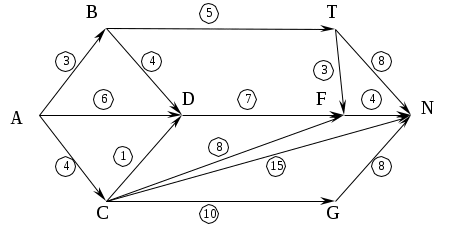
Определить кратчайший путь и его длину, предварительно пронумеровав вершины графа.
-
Пункты А и В связаны сетью дорог, проходящих через пункты С, D, Е, М, N. Стоимость проезда из пункта xi в xj указана на графе. Какова минимальная стоимость проезда из А и В?. Как проходит путь, соответствующий минимальным затратам?
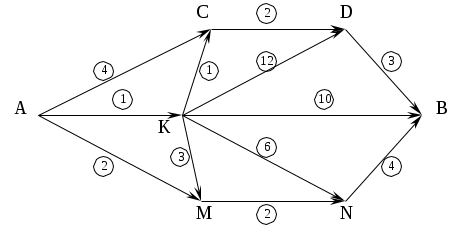
-
Для графов задач 6, 7 определить критический путь и критическое время.
-
Основу строительства объекта составляют 14 операций, последовательность выполнения которых задана графом. Продолжительность каждой из них указана на графе.
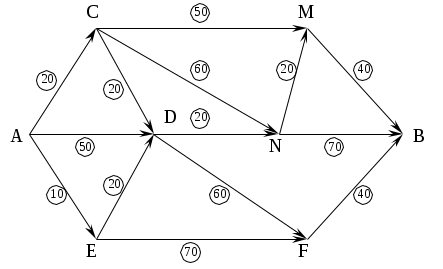
Определить скорейшее время завершения всего проекта. Какие операции не допускают запаздывания по времени?
-
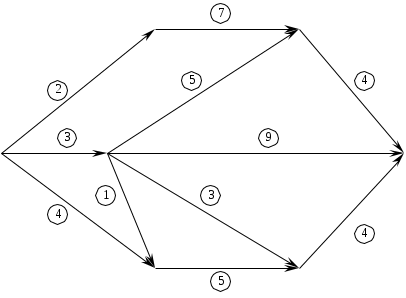
Найти кратчайший и длиннейший пути, соединяющие вход и выход графа, предварительно правильно пронумеровав вершины.
С писок рекомендуемой литературы
писок рекомендуемой литературы
-
Александров, П.С. Введение в теорию множеств и теорию функций. – М. : Наука, 1977 -
Балюкевич, Э.Л., Ковалева Л.Ф. Математическая логика и теория алгоритмов : учебное пособие. – М. : МГУЭСИ, 2007. -
Гаврилов, Г.П., Сапоженко, А.А. Задачи и упражнения по курсу «Дискретная математика». – М. : Наука, 1992 -
Грей, П. Логика, алгебра и базы данных. – М. : Машиностроение, 1989 -
Гиндикин, С.Г. Алгебра логики в задачах. – М. : Наука, 1972. -
Ерусалимский, Я.М. Дискретная математика. – М. : Вузовская книга, 2000. -
Колмогоров, А.Н., Фомин, С.В. Элементы теории функций и функционального анализа. – М. : Наука, 1989 -
Клини С. Математическая логика. – М. : Мир, 1973. -
Ковалева, Л.Ф., Данков, О.Ю., Горбовцов Г.Я., Мокеева И.К. Дискретная математика. – М. : МЭСИ, 1988. -
Нефедов, В.Н., Осипова В.А. Курс дискретной математики. – М. : МАИ, 1992. -
Новиков, Н. С. Элементы математической логики. – М. : Наука, 1973. -
Под редакцией Скорнякова Л.А. Общая алгебра. II. – М. : Наука, 1990г. -
Эдельман, С.Л. Математическая логика. – М. : Высшая школа, 1975. -
Яблонский, С.В. Введение в дискретную математику. – М. : Наука, 1979.
Интернет-ресурсы
-
www.osp.mesi.ru (сайт учебного процесса МЭСИ). Балюкевич Э.Л., Ковалева Л.Ф., Романников А.Н. Дискретная математика. -
www.booka.ru/booka_topic_6114?id=97427 Дискретная математика. Курс лекций.
Р
 уководство по изучению дисциплины
уководство по изучению дисциплиныСодержание основных тем.
-
Множества
1.1. Операции над множествами. Мощность множеств. Отображение множеств.
1.2. Отношения на множествах.
-
Математическая логика.
2.1. Алгебра высказываний.
2.2. Проблема разрешимости. Нормальные формы.
2.3. Исчисление высказываний.
2.4. Логика предикатов.
-
Теория графов.
3.1. Графы.
3.2. Деревья.
3.3. Экстремальные задачи на графах.
Тема 1. Множества
При изучении данной темы следует обратить внимание на то, что понятие «множество» является одним из основных во всех математических дисциплинах. Это можно проиллюстрировать большим количеством примеров как из школьной так и из вузовской – высшей математики.
