«Ғ.ДӘУКЕЕВ АТЫНДАҒЫ АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС УНИВЕРСИТЕТІ»

коммерциялық емес акционерлік қоғамы
«Автоматтандыру және басқару» кафедрасы

№1 Зертханалық жұмыс


Пәні: «Сызықты автоматты реттеу жүйелері»

Тақырыбы:«Басқару жүйелерінің математикалық сипаттамаларының формалары»

Мамандығы: Автоматтандыру және басқару

Орындаған: Амантай Гауһар

Тобы: АУТк-20-11 Нұсқа: 1

Қабылдаған: аға оқытушы Жүнайт А.

_____________ __________ «______» __________2022ж.

(бағасы) (қолы)

Алматы, 2022

Зертханалық жұмыс № 1 . Басқару жүйелерінің математикалық сипаттамаларының формалары.

Зертханалық жұмыс мақсаты: автоматты басқару жүйелерінің математикалық өрнектелуімен танысу.


1.1 Негізгі теориялық мағлұматтар
Басқару жүйесінің математикалық модельдерін көрсетудегі келесі формалары/6/:

1. 
   n–ші ретті дифференциалды теңдеу
   

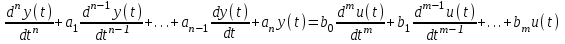, (1.1)

мұндағы t – үздіксіз уақыт;

t₀ – бастапқы уақыт;

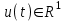–басқарылатын әсер;

y(t) – шығыс сигнал;

– үзбенің (жүйенің) физикалық параметрлерімен анықталатын тұрақты коэффициенттер;

n – , жүйенің дифференциалды теңдеу реті.

2. 
   Беріліс функциясы – Лаплас түрленуі бойынша шығыс шамасының Лаплас түрленуі бойынша кіріс шамасына қатысты нөлдік бастапқы шарттар кезінде
   

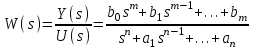, (1.2)

мұндағыs – Лаплас операторы;

y(s) и u(s) – сәйкесінше y(t) жәнеu(t) кескіні.

(2.2) теңдеуінің қорытындысы сипаттамалық полиномды анықтайды

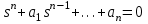, (1.3)

оның шешімінің түбірі болады

. (1.4)

(3.4) түбірлері беріліс функцияның полюстері деп аталады. Беріліс функция алымының түбірі беріліс функцияның

---

нөлдері деп аталады.

Жүйелерді беріліс функция түріне келтіру негізінен техникалық көпшілікке ие болады: зерттеуші соңғы нәтижесінде,тек физикалық айнымалылармен ғана емес, аралық этаптарда да жұмыс істейді, және жиі сынақты теориялық зерттеумен де алып жүру

мүмкіндігі бар. Бірақ осындай көрсетілімде әртүрлі жүйелер мен блоктардың

математикалық сипаттамалары сызықты жағдайда болса да, алымдар ретінен де және олардың беріліс функцияларының қорытындыларынан да тәуелділігі әртүрлі типті болып шығады.

3) Күй кеңістігіндегі дифференциалды теңдеу

Ол үшін 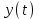шығыс айнымалылардың орнына 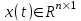күйлер айнымалыларын енгізеді. Бұл айнымалылардағы жүйе сипаттамасы бірінші реттік дифференциалды теңдеу жүйесімен беріледі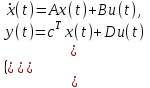
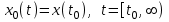, (1.5)

мұндағы 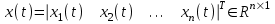– басқару объекті күйінің айнымалылар векторы;

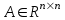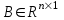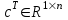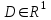, , , – күйлердің, басқарудың, бақылаудың (күйлер бойынша шығыс матрицасы), сәйкесінше басқару бойынша шығыс матрицалары болып табылады.

Егер (2.1) m=0 болса, онда n–ші ретті (3.1) теңдеуін жүйеге, n бірінші реттік дифференциалды теңдеулерден келтіруге болады

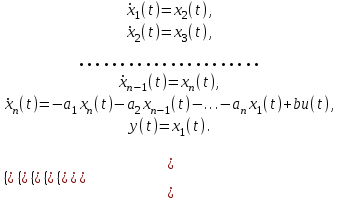(1.6)

(2.6) жүйенің матрицалық формасын, 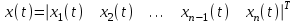векторын және төмендегі матрицаны енгізе алуға болады

.

(2.1) – да mnболса, онда дұрыс форма келесі түрге ие болады


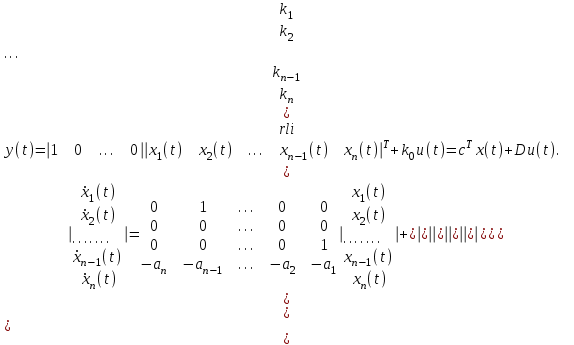(2.7)

_Мұнда

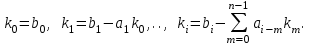
1.2 Нұсқа бойынша тапсырма

Дифференциалды теңдеу берілсін

---

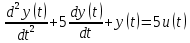
бастапқы шарттар кезінде (б.ш.)

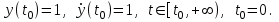
Тапсырма:

1. 
   MATLAB Simulink моделдеу ортасында (1.1) теңдеуінің құрылымдық сұлбасын 1-суретте келтірілгендей тұрғызу керек.
   

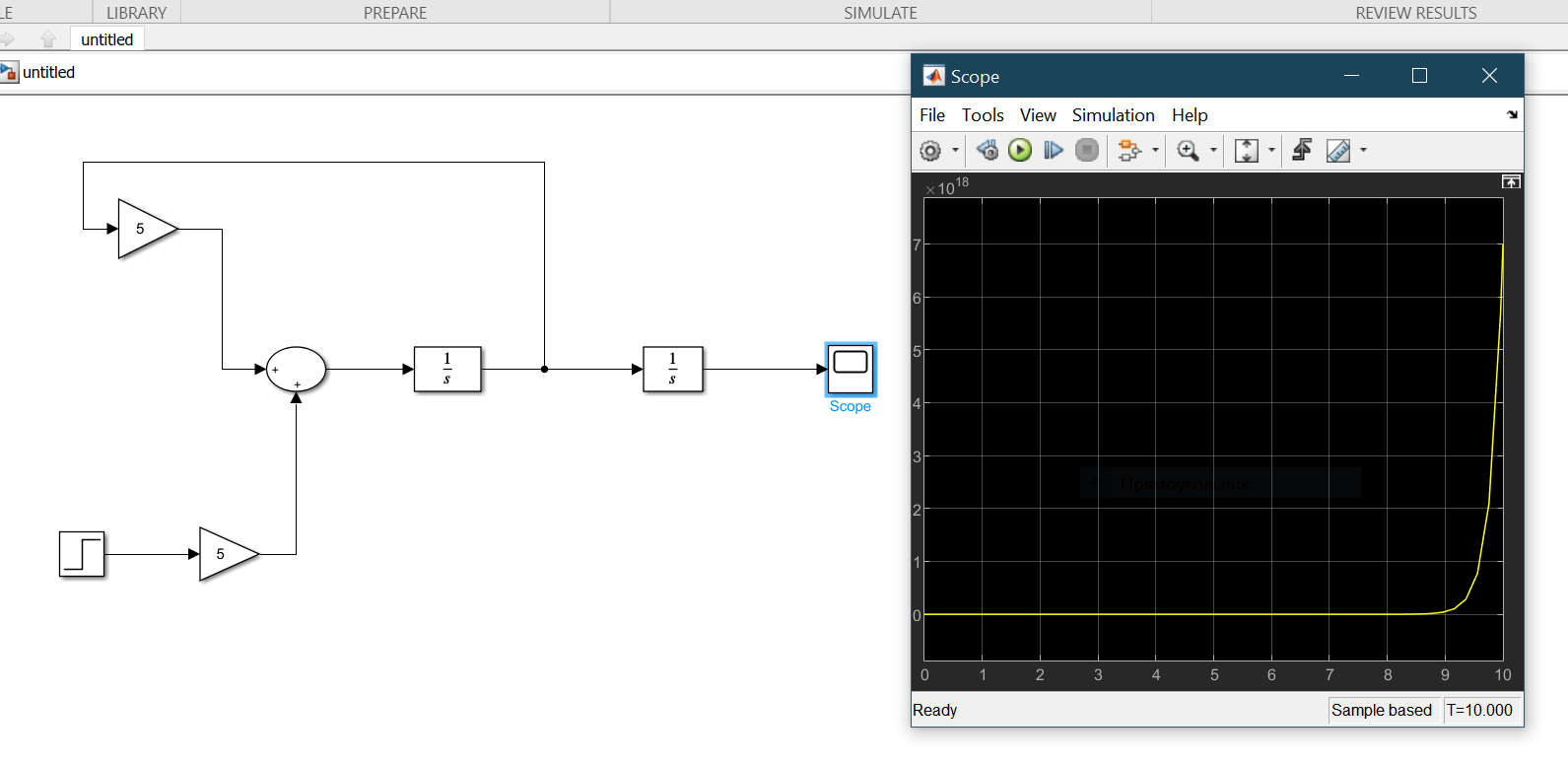
Cурет 1 – MATLAB Simulink –те (1.2) теңдеуін модельдеу сұлбасы

2. 
   (1.1) теңдеуді беріліс функциясы түрінде бейнелейік: Ол үшін келеcі жүйеге өтпелі үрдіс алайық, оның күйлер кеңістігі мен өтпелі функциясы келесідей түрде болады
   

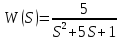
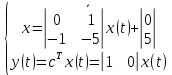
(1.3)
_{1Әдіс (MATLAB Simulink). Transfer Function (беріліс функциясы) және State Space (күйлер кеңістігі) блоктарын қолдану.}



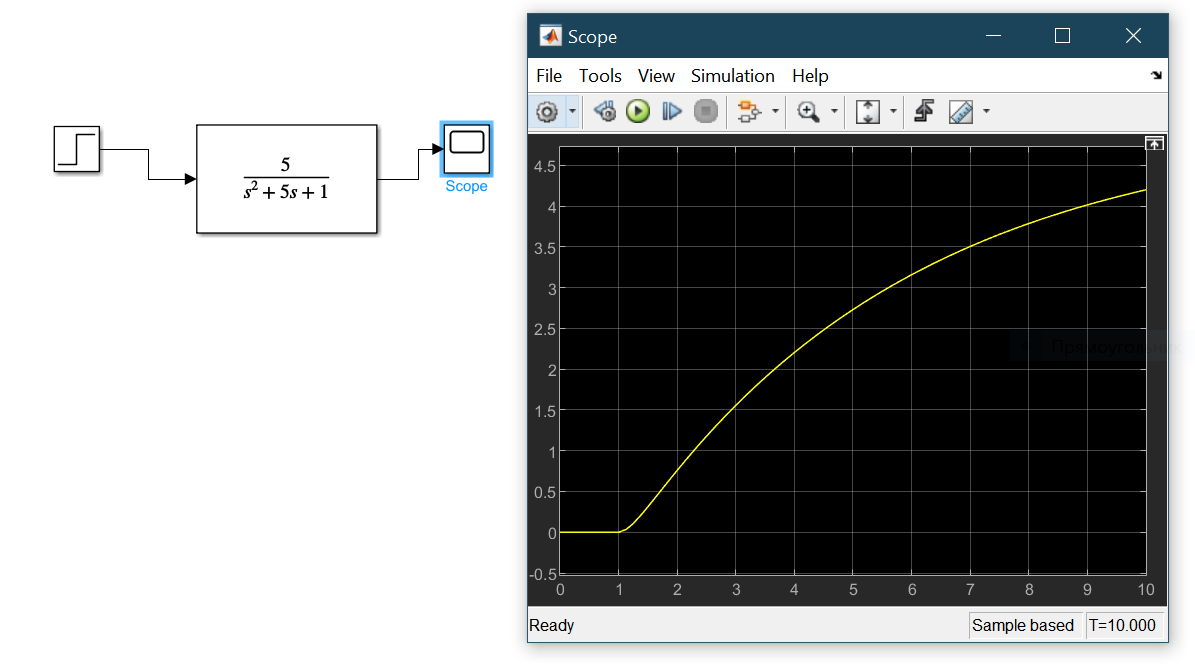
Сурет 2 – Transfer Function блогын қолдану




Сурет 3 – State Space блогын MATLAB-та қолдану

3. 
   2 Әдіс (MATLAB ортасында командалық режимде CST командасын қолдану). CST командасы жүйені LTI-модель беріліс функциясы немесе күйлер кеңістігінде анықтай алады, сонымен қатар сипаттама тұрғызуға арналған команда жиынтығы бар.
   

MATLAB командалық терезесінде w аттыLTI–объектті құрып (1.3) өтпелі сипаттама аламыз(сурет 4)

>> w=tf([5],[1 5 1])

w =
5

-------------

s^2 + 5 s + 1
Continuous-time transfer function.
>>step(w)

\


Сурет 4 – CST қолдану арқылы алынған өтпелі үрдіс
MATLAB командалық режимінде s атты LTI–объектті құрып (1.3) өтпелі сипаттама аламыз(сурет 5)

>> A=[0 1;-1 -5];

>> B=[0;5];

>> c=[1 0];

>> s=ss(A,B,c,0)

>>step(w)

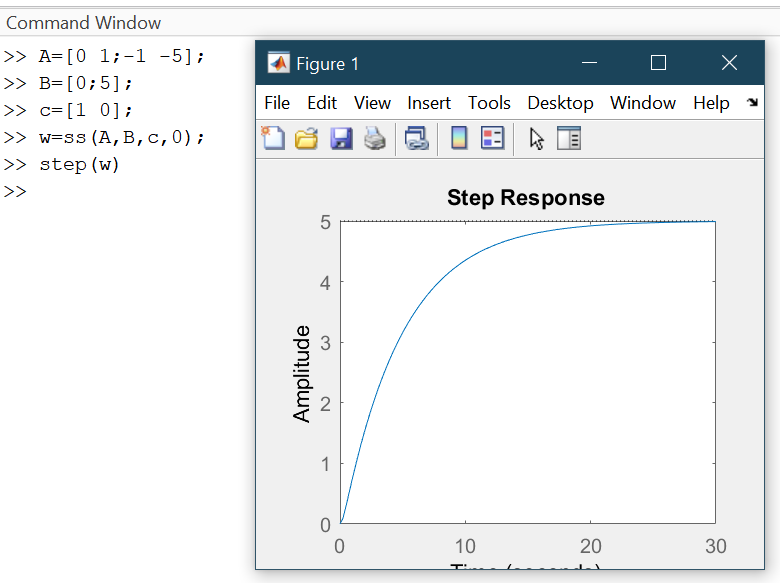
Сурет 5 – CST қолдану арқылы алынған өтпелі үрдіс
Қорытынды

Мен зертханалық жұмыста Автоматты басқару жүйелерінің математикалық өрнектелуімен таныстым. Бұл зертханалық жұмыста дифференциалды теңдеуді беріліс функциясына түрлендіріп үйрендім. Матлабтағы Simulink ортасында жұмыс жасадым. CST командаларымен жұмыс жасап үйрендім. Беріліс функциясының полюстерін және нолдерін анықтап үйрендім.

---

Бақылау сұрақтары

1. Автоматты басқару жүйелерінің математикалық модельдер көрінісі.

2. Беріліс функциясы.

3. Сипатталатын теңдеу.

4. Беріліс функциясының полюстері.

5. Автоматты басқару жүйесінің күйлер кеңістігіндегі математикалық моделі. Күйлер кеңістігіндегі қалыпты жағдайы.

6. Басқару жүйелерінің математикалық сипатталуының әр формасының артықшылығы.

1. 
   Автоматты басқару жүйелерінің математикалық модельдер көрінісі
   

Оларға жатады: n–ші ретті дифференциалды теңдеу, Беріліс функциясы, Күй кеңістігіндегі дифференциалды теңдеу

2. Беріліс функциясы.

Қоздыру операторының меншікті операторға қатынасы беріліс функциясы немесе операторлық формадағы беріліс функциясы деп аталады.Беріліс функциясы немесе Лаплас кескін формасындағы беріліс функциясы деп бастапқы нолдік шарттар кезінде шығыс шаманың кіріс шамаға қатынасын айтамыз.

3. Сипатталатын теңдеу.

 

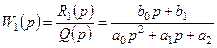
және z кіріс шамасы бойынша W₂(p) беріліс функциясы

 

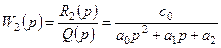
4. Беріліс функциясының полютері.

Мұндағы (2.16)   ,   кешенді көпмүшелік. Оны (2.2) өрнектегі В(р) және А(р) оператолық көпмүшеліктерде p операторды s операторымен алмастыру арқылы анықтауға болады. 2.16 теңдеудің бөліміндегі сипаттама теңдеуінің түбірі полюстер деп аталынады.

5. Автоматты басқару жүйесінің күйлер кеңістігіндегі математикалық моделі. Күйлер кеңістігіндегі қалыпты жағдайы.

6. Басқару жүйелерінің математикалық сипатталуының әр формасының артықшылығы.

Кіріс және шығыс сигналдарының арасындағы дифференциалдық және алгебралық байланыс теңдеулерінің жиынтығын жүйенің математикалық моделі деп атаймыз. Кіріс және шығыс сигналдарының туындылары нолге тең болған жағдайда, алгебралық теңдеулер орнықталған жағдайды сипаттайды және статика теңдеулері деп аталады.

Дифференциалдық теңдеулер кіріс әсерлердің өзгерісі кезіндегі уақыт бойынша жүйенің жағдайын сипаттайды. Олар 

---

динамика теңдеулері деп аталады.

---

Смотрите также файлы

• Планконспект проведения занятий по дисциплине Аварийноспасательные работы.docx

• Емтихан билеті 1 емтихан тапсырмасы.docx

• Определение показателей физических свойств грунтов.pdf

• Социальнопсихологический климат.docx

• Практическое задание Задание 1.docx