Файл: Решение задач по закону общей инверсии формула де Моргана.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.03.2024
Просмотров: 15
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа
Решение задач по закону общей инверсии формула де Моргана
Задача: используя законы алгебры логики составить тождественные упрощенные формы для следующих уравнений:
| Исходная формула | Полученная формула |
 | |
 | |
 | |
 | |
 | |
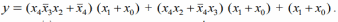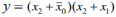Решение:
| Исходная формула | Полученная формула |
| Используем дистрибутивный закон и операцию с константой.  |  |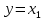
| Используем дистрибутивный закон и операцию с константой.  ( |  |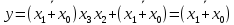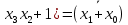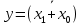
| Используем дистрибутивный закон и операцию с константой.  |  |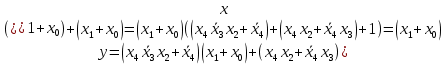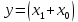
| Используем дистрибутивный закон и операцию с константой.  |  |
| Используем правило де Моргана.  |  |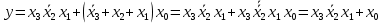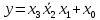
Контрольный вопрос: какими свойствами обладают логические функции дизъюнкции
, конъюнкции и инверсии.
Ответ:
Свойства конъюнкции:
- если хотя бы одно из подвыражений конъюнкции ложно на некотором наборе значений переменных, то и вся конъюнкция будет ложной для этого набора значений.
- если все выражения конъюнкции истинны на некотором наборе значений переменных, то и вся конъюнкция тоже будет истинна.
- значение всей конъюнкции сложного выражения не зависит от порядка записи подвыражений, к которым она применяется (как в математике умножение).
Свойства дизъюнкции:
- если хотя бы одно из подвыражений дизъюнкции истинно на некотором наборе значений переменных, то и вся дизъюнкция принимает истинное значение для данного набора подвыражений.
- если все выражения из некоторого списка дизъюнкции ложны на некотором наборе значений переменных, то и вся дизъюнкция этих выражений тоже ложна.
- значение всей дизъюнкции не зависит от порядка записи подвыражений (как в математике – сложение).
Свойства отрицания:
- «двойное отрицание»
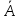является следствием суждения, то есть имеет место тавтология в формальной логике и равно самому значению в булевой логике.
