ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.04.2024
Просмотров: 36
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Методы возможных направлений
Оглавление
Введение 2
1. Метод Зойтендейка 3
2. Построение возможных направлений спуска 6
3. Алгоритм метода Зойтендейка в случае линейных ограничений 9
4. Алгоритм Зойтендейка в случае нелинейных ограничений-неравенств 13
5. Модификация метода возможных направлений 18
Заключение 22
Список использованных источников 23
Введение
Методы возможных направлений – наиболее исследованный класс методов выпуклого программирования (задачи выпуклого программирования – это такие задачи нелинейного программирования, в которых целевые функции и функции ограничений выпуклы).
Подробное описание данных методов было произведено в работах Зойтендейка1.
Хотя сходимость к глобальному минимуму может быть доказана только в случаях задач выпуклого программирования, тем не менее методы возможных направлений сходятся к локальному минимуму и в применении к задачам нелинейного программирования вообще.
Цель данной работы - рассмотреть сущность методов возможных направлений.
1. Метод Зойтендейка
Типичным представителем класса методов возможных направлений является метод Зойтендейка. На каждой итерации метода находят возможное направление спуска, а затем проводят оптимизацию вдоль этого направления. Для изложения идеи метода введем ряд необходимых понятий2:
Рассмотрим задачу минимизаци при условии, что , где – непустое множество.
Ненулевой вектор называется возможным направлением в точке , если существует такое , что для всех .
Вектор называется возможным направлением спуска в точке , если существует такое , что и для всех .
Сначала рассмотрим случай, когда ограничения линейные и задача НП имеет вид:
минимизировать (1)
при условиях (2)
(3)
где – матрица порядка ;
– матрица порядка ;
— -мерный вектор;
— -мерный вектор.
Справедливо следующее утверждение.
Лемма 1. Рассмотрим задачу минимизаци (1) - (3). Пусть - допустимая точка и предположим, что , где , а .
Ненулевой вектор является возможным направлением в точке в том и только в том случае, если и . Если, кроме того, , то является возможным направлением спуска.
Проиллюстрируем геометрически множество возможных направлений спуска на следующем примере.
Пример 1. Минимизировать при условиях
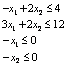
Выберем и заметим, что первые два ограничения являются активными в этой точке. В частности, матрица из вышеприведенной леммы 1, равна . Следовательно, вектор является возможным направлением тогда и только тогда, когда т.е. в том случае, если
На рис. 1. изображена совокупность этих направлений, образующая конус возможных направлений. Здесь 1 – конус возможных направлений; 2 – конус возможных направлений спуска; 3 – линии уровня целевой функции; 4 – полупространство направлений спуска.
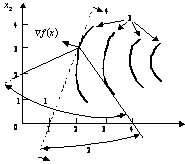
Рисунок 1
Если вектор удовлетворяет неравенству , то он является направлением спуска. Таким образом, совокупность возможных направлений спуска определяется открытым полупространством . Пересечение конуса возможных направлений с этим полупространством задает множество всех возможных направлений спуска.
2. Построение возможных направлений спуска
Пусть задана текущая допустимая точка x. Как показано в лемме 1, ненулевой вектор будет возможным направлением спуска, если . Естественный подход к построению такого направления заключается в минимизации при условиях: . Однако, если существует такой вектор , что , и выполняются условия а) и б), то оптимальное значение целевой функции сформулированной задачи равно – , так как ограничениям этой задачи удовлетворяет любой вектор , где – любое большое число.
Следовательно, в задачу должно быть включено условие, которое бы ограничивало вектор . Такое ограничение называют нормирующим. Возможны различные формы нормирующего ограничения. Ниже приведем три задачи отыскания (наилучшего) направления спуска, в каждой из которых используются различные условия нормировки3:
Задача : минимизировать
при условиях
Задача : минимизировать
при условиях
Задача : минимизировать
при условиях
Задачи и являются задачами линейного программирования и, следовательно, их можно решить симплекс-методом.
Так как является допустимой точкой в каждой из приведенных выше задач, а значение целевой функции в этой точке равно 0, то ее оптимальное значение в задачах , , не может быть положительным. Если минимальное значение ц.ф. в задачах , , отрицательно, то по лемме 6.1 нами построено возможное направление спуска. С другой стороны, если минимальное значение целевой функции равно нулю, то, как будет показано ниже, точка x является точкой Куна-Таккера.
Лемма 2. Рассмотрим задачу минимизаци приусловиях . Пусть – допустимая точка, в которой , где 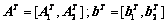 . Вектор является точкой Куна-Таккера тогда и только тогда, когда оптимальное значение целевой функции в задачах , , равно нулю.
. Вектор является точкой Куна-Таккера тогда и только тогда, когда оптимальное значение целевой функции в задачах , , равно нулю.
Доказательство. Как следует из теоремы Куна-Таккера, будет точкой Куна-Таккера тогда и только тогда, когда существуют векторы такие, что
. (4)
Согласно следствию из леммы Фаркаша система (4) разрешима тогда и только тогда, когда система неравенств не имеет решений, т.е. когда оптимальное значение целевой функции в задачах , , равно нулю.
Итак, мы показали, как найти возможное направление спуска.
Пусть теперь – текущая точка; – возможное направление спуска. В качестве следующей точки выбирается , где длина шага определяется из решения следующей задачи одномерной оптимизации:
минимизировать по (5)
при условиях
, (6)
. (7)
Предположим, что . Тогда задачу (5) - (7) можно упростить следующим образом. Заметим, что . Значит, ограничение (7) излишне. Так как , то для всех . Итак, остается только одно ограничение , и задача оптимизации (5) - (7) приводится к следующей задаче одномерной оптимизации:
минимизировать по (8)
при условии
,
где 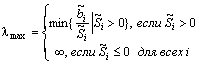 (9)
(9)
. (10)
3. Алгоритм метода Зойтендейка в случае линейных ограничений
Пусть требуется найти при условиях .
Алгоритм метода состоит из предварительного и основного этапов. Последний в свою очередь состоит из однотипных итераций4:
Предварительный этап. Найти начальную допустимую точку, для которой . Положить и перейти к основному этапу.
Основной этап. -я итерация. Первый шаг. Пусть задан вектор . Предположим, что и . В качестве возможного направления спуска взять оптимальное решение следующей задачи:
минимизировать (11)
при условиях
(12)
. (13)
Если , то остановиться, и – оптимальное решение (точка Куна-Таккера). В противном случае перейти ко второму шагу.
Второй шаг. Положить равным оптимальному решению приведенной ниже задачи одномерной оптимизации:
минимизировать
при условии ,
где задается формулой (9).
Для решения этой задачи можно применить любой метод одномерного поиска, например метод Фибоначчи.
Вычислить , определить новое множество активных ограничений для решения и переопределить и . Заменить на и перейти к первому шагу следующей итерации.
Рассмотрим задачу, в которой допустимая область задается системой ограничений-неравенств нелинейного типа:
минимизировать (14)
при условиях (15)
В следующей теореме формулируются достаточные условия, при которых вектор является возможным направлением спуска.
Теорема 2. Рассмотрим задачу нелинейного программирования (14), (15). Пусть – допустимая точка, а – множество индексов активных в этой точке ограничений, т.е. . Предположим, кроме того, что функции для дифференцируемы в точке , а функции для непрерывны в этой точке. Если , при , то вектор является возможным направлением спуска.
Доказательство. Пусть вектор удовлетворяет неравенствам , при . Сначала укажем, что для выполняются неравенства и так как непрерывны в точке , то для достаточно малых . В силу дифференцируемости функции , имеем , где при . Так как , то при достаточно малых . Следовательно, точка допустима для малых значений . Аналогично из следует, что для достаточно малых .
Таким образом, вектор является возможным направлением спуска.
На рис. 2 показана совокупность возможных направлений в точке . Здесь использованы такие обозначения: 1 – первое ограничение, 2 – третье ограничение, 3 – четвертое ограничение, 4 – второе ограничение, 5 – возможные направления спуска, 6 – линии уровня целевой функции. Вектор , удовлетворяющий равенству , является касательным к кривой линии (или поверхности) . Поскольку функции нелинейны, то движение вдоль такого вектора может привести в недопустимую точку, что вынуждает требовать выполнения строгого неравенства .
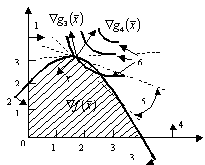
Рисунок 2
Чтобы найти вектор , удовлетворяющий неравенствам , для , вполне естественно минимизировать максимум из величин и для . Обозначим этот максимум через . Вводя нормирующие условия , для всех , приходим к следующей вспомогательной задаче нахождения возможного направления спуска:
минимизировать (16)
при условиях
, (17)
, (18)
. (19)
Пусть – оптимальное решение этой задачи ЛП. Если , то, очевидно, – возможное направление спуска. Если же , то, как будет показано ниже, точка является точкой Куна-Таккера.
Докажем это утверждение. Оптимальное значение целевой функции в задаче (16) - (19) равно нулю тогда и только тогда, когда система неравенств , при несовместна. Но, согласно следствию из леммы Фаркаша, для того чтобы эта система не имела решения, необходимо и достаточно, чтобы существовали такие числа , что
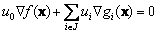 (20)
(20)
и либо , либо для некоторого , а это одно из условий оптимальности теоремы Куна-Таккера.
4. Алгоритм Зойтендейка в случае нелинейных ограничений-неравенств
Далее рассмотрим алгоритм Зойтендейка при нелинейных ограничениях-неравненствах5:
Предварительный этап. Выбрать точку , для которой . Положить и перейти к основному этапу.
Основной этап. Первый шаг. Положить и решить задачу:
минимизировать (20)
при условиях
, (21)
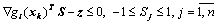 . (22)
. (22)
Пусть – оптимальное решение задачи (20) – (22). Если , то конец алгоритма и точка – оптимальное решение такой задачи одномерной оптимизации. Если , то перейти ко второму шагу.
Второй шаг.
минимизировать (23)
при условии , (24)
где 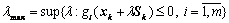 . (25)
. (25)
Положить , заменить на и перейти к первому шагу следующей итерации.
Пример 4. Рассмотрим задачу:
минимизировать
при условиях
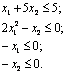
Будем решать эту задачу методом Зойтендейка, начиная поиск из точки . Заметим, что
Первая итерация. Первый шаг. В точке имеем , а множество индексов активных ограничений есть . При этом . Задача нахождения возможного направления имеет вид
минимизировать
при условиях 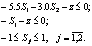
Можно проверить, решая эту задачу симплекс-методом, что оптимальным решением этой задачи является вектор и .
Второй шаг. Линейный поиск. Любая точка по направлению из точки может быть представлена в виде , а соответствующее ей значение целевой функции равно . Максимальное значение , для которого точка остается допустимой, равно . Итак, решаем задачу одномерной минимизации:
минимизировать
при условии
Оптимальное значение . Итак, .
Вторая итерация. Первый шаг. В точке имеем . Активных ограничений в этой точке нет, поэтому задача определения направления спуска имеет вид:
минимизировать z
при условиях 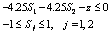
Оптимальным решением является вектор , а .
Второй шаг. Легко проверить, что , при котором точка допустима, равна 0.3472. При этом активным становится ограничение . Оптимальное значение находим в результате решения задачи:
минимизировать z
при условии
Оно равно 0.3472, так что . Остальные итерации проводятся аналогично. Результаты вычислений на первых четырех итерациях метода приведены в табл. 1.
Таблица 1
Методы возможных направлений
Оглавление
Введение 2
1. Метод Зойтендейка 3
2. Построение возможных направлений спуска 6
3. Алгоритм метода Зойтендейка в случае линейных ограничений 9
4. Алгоритм Зойтендейка в случае нелинейных ограничений-неравенств 13
5. Модификация метода возможных направлений 18
Заключение 22
Список использованных источников 23
Введение
Методы возможных направлений – наиболее исследованный класс методов выпуклого программирования (задачи выпуклого программирования – это такие задачи нелинейного программирования, в которых целевые функции и функции ограничений выпуклы).
Подробное описание данных методов было произведено в работах Зойтендейка1.
Хотя сходимость к глобальному минимуму может быть доказана только в случаях задач выпуклого программирования, тем не менее методы возможных направлений сходятся к локальному минимуму и в применении к задачам нелинейного программирования вообще.
Цель данной работы - рассмотреть сущность методов возможных направлений.
1. Метод Зойтендейка
Типичным представителем класса методов возможных направлений является метод Зойтендейка. На каждой итерации метода находят возможное направление спуска, а затем проводят оптимизацию вдоль этого направления. Для изложения идеи метода введем ряд необходимых понятий2:
Рассмотрим задачу минимизаци при условии, что , где – непустое множество.
Ненулевой вектор называется возможным направлением в точке , если существует такое , что для всех .
Вектор называется возможным направлением спуска в точке , если существует такое , что и для всех .
Сначала рассмотрим случай, когда ограничения линейные и задача НП имеет вид:
минимизировать (1)
при условиях (2)
(3)
где – матрица порядка ;
– матрица порядка ;
— -мерный вектор;
— -мерный вектор.
Справедливо следующее утверждение.
Лемма 1. Рассмотрим задачу минимизаци (1) - (3). Пусть - допустимая точка и предположим, что , где , а .
Ненулевой вектор является возможным направлением в точке в том и только в том случае, если и . Если, кроме того, , то является возможным направлением спуска.
Проиллюстрируем геометрически множество возможных направлений спуска на следующем примере.
Пример 1. Минимизировать при условиях
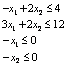
Выберем и заметим, что первые два ограничения являются активными в этой точке. В частности, матрица из вышеприведенной леммы 1, равна . Следовательно, вектор является возможным направлением тогда и только тогда, когда т.е. в том случае, если
На рис. 1. изображена совокупность этих направлений, образующая конус возможных направлений. Здесь 1 – конус возможных направлений; 2 – конус возможных направлений спуска; 3 – линии уровня целевой функции; 4 – полупространство направлений спуска.

Рисунок 1
Если вектор удовлетворяет неравенству , то он является направлением спуска. Таким образом, совокупность возможных направлений спуска определяется открытым полупространством . Пересечение конуса возможных направлений с этим полупространством задает множество всех возможных направлений спуска.
2. Построение возможных направлений спуска
Пусть задана текущая допустимая точка x. Как показано в лемме 1, ненулевой вектор будет возможным направлением спуска, если . Естественный подход к построению такого направления заключается в минимизации при условиях: . Однако, если существует такой вектор , что , и выполняются условия а) и б), то оптимальное значение целевой функции сформулированной задачи равно – , так как ограничениям этой задачи удовлетворяет любой вектор , где – любое большое число.
Следовательно, в задачу должно быть включено условие, которое бы ограничивало вектор . Такое ограничение называют нормирующим. Возможны различные формы нормирующего ограничения. Ниже приведем три задачи отыскания (наилучшего) направления спуска, в каждой из которых используются различные условия нормировки3:
Задача : минимизировать
при условиях
Задача : минимизировать
при условиях
Задача : минимизировать
при условиях
Задачи и являются задачами линейного программирования и, следовательно, их можно решить симплекс-методом.
Так как является допустимой точкой в каждой из приведенных выше задач, а значение целевой функции в этой точке равно 0, то ее оптимальное значение в задачах , , не может быть положительным. Если минимальное значение ц.ф. в задачах , , отрицательно, то по лемме 6.1 нами построено возможное направление спуска. С другой стороны, если минимальное значение целевой функции равно нулю, то, как будет показано ниже, точка x является точкой Куна-Таккера.
Лемма 2. Рассмотрим задачу минимизаци приусловиях . Пусть – допустимая точка, в которой , где 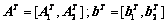 . Вектор является точкой Куна-Таккера тогда и только тогда, когда оптимальное значение целевой функции в задачах , , равно нулю.
. Вектор является точкой Куна-Таккера тогда и только тогда, когда оптимальное значение целевой функции в задачах , , равно нулю.
Доказательство. Как следует из теоремы Куна-Таккера, будет точкой Куна-Таккера тогда и только тогда, когда существуют векторы такие, что
. (4)
Согласно следствию из леммы Фаркаша система (4) разрешима тогда и только тогда, когда система неравенств не имеет решений, т.е. когда оптимальное значение целевой функции в задачах , , равно нулю.
Итак, мы показали, как найти возможное направление спуска.
Пусть теперь – текущая точка; – возможное направление спуска. В качестве следующей точки выбирается , где длина шага определяется из решения следующей задачи одномерной оптимизации:
минимизировать по (5)
при условиях
, (6)
. (7)
Предположим, что . Тогда задачу (5) - (7) можно упростить следующим образом. Заметим, что . Значит, ограничение (7) излишне. Так как , то для всех . Итак, остается только одно ограничение , и задача оптимизации (5) - (7) приводится к следующей задаче одномерной оптимизации:
минимизировать по (8)
при условии
,
где 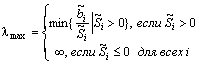 (9)
(9)
. (10)
3. Алгоритм метода Зойтендейка в случае линейных ограничений
Пусть требуется найти при условиях .
Алгоритм метода состоит из предварительного и основного этапов. Последний в свою очередь состоит из однотипных итераций4:
Предварительный этап. Найти начальную допустимую точку, для которой . Положить и перейти к основному этапу.
Основной этап. -я итерация. Первый шаг. Пусть задан вектор . Предположим, что и . В качестве возможного направления спуска взять оптимальное решение следующей задачи:
минимизировать (11)
при условиях
(12)
. (13)
Если , то остановиться, и – оптимальное решение (точка Куна-Таккера). В противном случае перейти ко второму шагу.
Второй шаг. Положить равным оптимальному решению приведенной ниже задачи одномерной оптимизации:
минимизировать
при условии ,
где задается формулой (9).
Для решения этой задачи можно применить любой метод одномерного поиска, например метод Фибоначчи.
Вычислить , определить новое множество активных ограничений для решения и переопределить и . Заменить на и перейти к первому шагу следующей итерации.
Рассмотрим задачу, в которой допустимая область задается системой ограничений-неравенств нелинейного типа:
минимизировать (14)
при условиях (15)
В следующей теореме формулируются достаточные условия, при которых вектор является возможным направлением спуска.
Теорема 2. Рассмотрим задачу нелинейного программирования (14), (15). Пусть – допустимая точка, а – множество индексов активных в этой точке ограничений, т.е. . Предположим, кроме того, что функции для дифференцируемы в точке , а функции для непрерывны в этой точке. Если , при , то вектор является возможным направлением спуска.
Доказательство. Пусть вектор удовлетворяет неравенствам , при . Сначала укажем, что для выполняются неравенства и так как непрерывны в точке , то для достаточно малых . В силу дифференцируемости функции , имеем , где при . Так как , то при достаточно малых . Следовательно, точка допустима для малых значений . Аналогично из следует, что для достаточно малых .
Таким образом, вектор является возможным направлением спуска.
На рис. 2 показана совокупность возможных направлений в точке . Здесь использованы такие обозначения: 1 – первое ограничение, 2 – третье ограничение, 3 – четвертое ограничение, 4 – второе ограничение, 5 – возможные направления спуска, 6 – линии уровня целевой функции. Вектор , удовлетворяющий равенству , является касательным к кривой линии (или поверхности) . Поскольку функции нелинейны, то движение вдоль такого вектора может привести в недопустимую точку, что вынуждает требовать выполнения строгого неравенства .

Рисунок 2
Чтобы найти вектор , удовлетворяющий неравенствам , для , вполне естественно минимизировать максимум из величин и для . Обозначим этот максимум через . Вводя нормирующие условия , для всех , приходим к следующей вспомогательной задаче нахождения возможного направления спуска:
минимизировать (16)
при условиях
, (17)
, (18)
. (19)
Пусть – оптимальное решение этой задачи ЛП. Если , то, очевидно, – возможное направление спуска. Если же , то, как будет показано ниже, точка является точкой Куна-Таккера.
Докажем это утверждение. Оптимальное значение целевой функции в задаче (16) - (19) равно нулю тогда и только тогда, когда система неравенств , при несовместна. Но, согласно следствию из леммы Фаркаша, для того чтобы эта система не имела решения, необходимо и достаточно, чтобы существовали такие числа , что
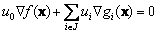 (20)
(20)
и либо , либо для некоторого , а это одно из условий оптимальности теоремы Куна-Таккера.
4. Алгоритм Зойтендейка в случае нелинейных ограничений-неравенств
Далее рассмотрим алгоритм Зойтендейка при нелинейных ограничениях-неравненствах5:
Предварительный этап. Выбрать точку , для которой . Положить и перейти к основному этапу.
Основной этап. Первый шаг. Положить и решить задачу:
минимизировать (20)
при условиях
, (21)
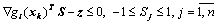 . (22)
. (22)
Пусть – оптимальное решение задачи (20) – (22). Если , то конец алгоритма и точка – оптимальное решение такой задачи одномерной оптимизации. Если , то перейти ко второму шагу.
Второй шаг.
минимизировать (23)
при условии , (24)
где 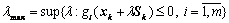 . (25)
. (25)
Положить , заменить на и перейти к первому шагу следующей итерации.
Пример 4. Рассмотрим задачу:
минимизировать
при условиях
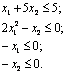
Будем решать эту задачу методом Зойтендейка, начиная поиск из точки . Заметим, что
Первая итерация. Первый шаг. В точке имеем , а множество индексов активных ограничений есть . При этом . Задача нахождения возможного направления имеет вид
минимизировать
при условиях 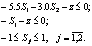
Можно проверить, решая эту задачу симплекс-методом, что оптимальным решением этой задачи является вектор и .
Второй шаг. Линейный поиск. Любая точка по направлению из точки может быть представлена в виде , а соответствующее ей значение целевой функции равно . Максимальное значение , для которого точка остается допустимой, равно . Итак, решаем задачу одномерной минимизации:
минимизировать
при условии
Оптимальное значение . Итак, .
Вторая итерация. Первый шаг. В точке имеем . Активных ограничений в этой точке нет, поэтому задача определения направления спуска имеет вид:
минимизировать z
при условиях 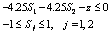
Оптимальным решением является вектор , а .
Второй шаг. Легко проверить, что , при котором точка допустима, равна 0.3472. При этом активным становится ограничение . Оптимальное значение находим в результате решения задачи:
минимизировать z
при условии
Оно равно 0.3472, так что . Остальные итерации проводятся аналогично. Результаты вычислений на первых четырех итерациях метода приведены в табл. 1.
Таблица 1
Методы возможных направлений
Оглавление
Введение 2
1. Метод Зойтендейка 3
2. Построение возможных направлений спуска 6
3. Алгоритм метода Зойтендейка в случае линейных ограничений 9
4. Алгоритм Зойтендейка в случае нелинейных ограничений-неравенств 13
5. Модификация метода возможных направлений 18
Заключение 22
Список использованных источников 23
Введение
Методы возможных направлений – наиболее исследованный класс методов выпуклого программирования (задачи выпуклого программирования – это такие задачи нелинейного программирования, в которых целевые функции и функции ограничений выпуклы).
Подробное описание данных методов было произведено в работах Зойтендейка1.
Хотя сходимость к глобальному минимуму может быть доказана только в случаях задач выпуклого программирования, тем не менее методы возможных направлений сходятся к локальному минимуму и в применении к задачам нелинейного программирования вообще.
Цель данной работы - рассмотреть сущность методов возможных направлений.
1. Метод Зойтендейка
Типичным представителем класса методов возможных направлений является метод Зойтендейка. На каждой итерации метода находят возможное направление спуска, а затем проводят оптимизацию вдоль этого направления. Для изложения идеи метода введем ряд необходимых понятий2:
Рассмотрим задачу минимизаци при условии, что , где – непустое множество.
Ненулевой вектор называется возможным направлением в точке , если существует такое , что для всех .
Вектор называется возможным направлением спуска в точке , если существует такое , что и для всех .
Сначала рассмотрим случай, когда ограничения линейные и задача НП имеет вид:
минимизировать (1)
при условиях (2)
(3)
где – матрица порядка ;
– матрица порядка ;
— -мерный вектор;
— -мерный вектор.
Справедливо следующее утверждение.
Лемма 1. Рассмотрим задачу минимизаци (1) - (3). Пусть - допустимая точка и предположим, что , где , а .
Ненулевой вектор является возможным направлением в точке в том и только в том случае, если и . Если, кроме того, , то является возможным направлением спуска.
Проиллюстрируем геометрически множество возможных направлений спуска на следующем примере.
Пример 1. Минимизировать при условиях
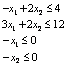
Выберем и заметим, что первые два ограничения являются активными в этой точке. В частности, матрица из вышеприведенной леммы 1, равна . Следовательно, вектор является возможным направлением тогда и только тогда, когда т.е. в том случае, если
На рис. 1. изображена совокупность этих направлений, образующая конус возможных направлений. Здесь 1 – конус возможных направлений; 2 – конус возможных направлений спуска; 3 – линии уровня целевой функции; 4 – полупространство направлений спуска.

Рисунок 1
Если вектор удовлетворяет неравенству , то он является направлением спуска. Таким образом, совокупность возможных направлений спуска определяется открытым полупространством . Пересечение конуса возможных направлений с этим полупространством задает множество всех возможных направлений спуска.
2. Построение возможных направлений спуска
Пусть задана текущая допустимая точка x. Как показано в лемме 1, ненулевой вектор будет возможным направлением спуска, если . Естественный подход к построению такого направления заключается в минимизации при условиях: . Однако, если существует такой вектор , что , и выполняются условия а) и б), то оптимальное значение целевой функции сформулированной задачи равно – , так как ограничениям этой задачи удовлетворяет любой вектор , где – любое большое число.
Следовательно, в задачу должно быть включено условие, которое бы ограничивало вектор . Такое ограничение называют нормирующим. Возможны различные формы нормирующего ограничения. Ниже приведем три задачи отыскания (наилучшего) направления спуска, в каждой из которых используются различные условия нормировки3:
Задача : минимизировать
при условиях
Задача : минимизировать
при условиях
Задача : минимизировать
при условиях
Задачи и являются задачами линейного программирования и, следовательно, их можно решить симплекс-методом.
Так как является допустимой точкой в каждой из приведенных выше задач, а значение целевой функции в этой точке равно 0, то ее оптимальное значение в задачах , , не может быть положительным. Если минимальное значение ц.ф. в задачах , , отрицательно, то по лемме 6.1 нами построено возможное направление спуска. С другой стороны, если минимальное значение целевой функции равно нулю, то, как будет показано ниже, точка x является точкой Куна-Таккера.
Лемма 2. Рассмотрим задачу минимизаци приусловиях . Пусть – допустимая точка, в которой , где
Доказательство. Как следует из теоремы Куна-Таккера, будет точкой Куна-Таккера тогда и только тогда, когда существуют векторы такие, что
. (4)
Согласно следствию из леммы Фаркаша система (4) разрешима тогда и только тогда, когда система неравенств не имеет решений, т.е. когда оптимальное значение целевой функции в задачах , , равно нулю.
Итак, мы показали, как найти возможное направление спуска.
Пусть теперь – текущая точка; – возможное направление спуска. В качестве следующей точки выбирается , где длина шага определяется из решения следующей задачи одномерной оптимизации:
минимизировать по (5)
при условиях
, (6)
. (7)
Предположим, что . Тогда задачу (5) - (7) можно упростить следующим образом. Заметим, что . Значит, ограничение (7) излишне. Так как , то для всех . Итак, остается только одно ограничение , и задача оптимизации (5) - (7) приводится к следующей задаче одномерной оптимизации:
минимизировать по (8)
при условии
,
где
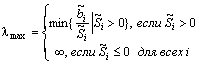 (9)
(9). (10)
3. Алгоритм метода Зойтендейка в случае линейных ограничений
Пусть требуется найти при условиях .
Алгоритм метода состоит из предварительного и основного этапов. Последний в свою очередь состоит из однотипных итераций4:
Предварительный этап. Найти начальную допустимую точку, для которой . Положить и перейти к основному этапу.
Основной этап. -я итерация. Первый шаг. Пусть задан вектор . Предположим, что и . В качестве возможного направления спуска взять оптимальное решение следующей задачи:
минимизировать (11)
при условиях
(12)
. (13)
Если , то остановиться, и – оптимальное решение (точка Куна-Таккера). В противном случае перейти ко второму шагу.
Второй шаг. Положить равным оптимальному решению приведенной ниже задачи одномерной оптимизации:
минимизировать
при условии ,
где задается формулой (9).
Для решения этой задачи можно применить любой метод одномерного поиска, например метод Фибоначчи.
Вычислить , определить новое множество активных ограничений для решения и переопределить и . Заменить на и перейти к первому шагу следующей итерации.
Рассмотрим задачу, в которой допустимая область задается системой ограничений-неравенств нелинейного типа:
минимизировать (14)
при условиях (15)
В следующей теореме формулируются достаточные условия, при которых вектор является возможным направлением спуска.
Теорема 2. Рассмотрим задачу нелинейного программирования (14), (15). Пусть – допустимая точка, а – множество индексов активных в этой точке ограничений, т.е. . Предположим, кроме того, что функции для дифференцируемы в точке , а функции для непрерывны в этой точке. Если , при , то вектор является возможным направлением спуска.
Доказательство. Пусть вектор удовлетворяет неравенствам , при . Сначала укажем, что для выполняются неравенства и так как непрерывны в точке , то для достаточно малых . В силу дифференцируемости функции , имеем , где при . Так как , то при достаточно малых . Следовательно, точка допустима для малых значений . Аналогично из следует, что для достаточно малых .
Таким образом, вектор является возможным направлением спуска.
На рис. 2 показана совокупность возможных направлений в точке . Здесь использованы такие обозначения: 1 – первое ограничение, 2 – третье ограничение, 3 – четвертое ограничение, 4 – второе ограничение, 5 – возможные направления спуска, 6 – линии уровня целевой функции. Вектор , удовлетворяющий равенству , является касательным к кривой линии (или поверхности) . Поскольку функции нелинейны, то движение вдоль такого вектора может привести в недопустимую точку, что вынуждает требовать выполнения строгого неравенства .

Рисунок 2
Чтобы найти вектор , удовлетворяющий неравенствам , для , вполне естественно минимизировать максимум из величин и для . Обозначим этот максимум через . Вводя нормирующие условия , для всех , приходим к следующей вспомогательной задаче нахождения возможного направления спуска:
минимизировать (16)
при условиях
, (17)
, (18)
. (19)
Пусть – оптимальное решение этой задачи ЛП. Если , то, очевидно, – возможное направление спуска. Если же , то, как будет показано ниже, точка является точкой Куна-Таккера.
Докажем это утверждение. Оптимальное значение целевой функции в задаче (16) - (19) равно нулю тогда и только тогда, когда система неравенств , при несовместна. Но, согласно следствию из леммы Фаркаша, для того чтобы эта система не имела решения, необходимо и достаточно, чтобы существовали такие числа , что
и либо , либо для некоторого , а это одно из условий оптимальности теоремы Куна-Таккера.
4. Алгоритм Зойтендейка в случае нелинейных ограничений-неравенств
Далее рассмотрим алгоритм Зойтендейка при нелинейных ограничениях-неравненствах5:
Предварительный этап. Выбрать точку , для которой . Положить и перейти к основному этапу.
Основной этап. Первый шаг. Положить и решить задачу:
минимизировать (20)
при условиях
, (21)
Пусть – оптимальное решение задачи (20) – (22). Если , то конец алгоритма и точка – оптимальное решение такой задачи одномерной оптимизации. Если , то перейти ко второму шагу.
Второй шаг.
минимизировать (23)
при условии , (24)
где
Положить , заменить на и перейти к первому шагу следующей итерации.
Пример 4. Рассмотрим задачу:
минимизировать
при условиях
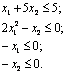
Будем решать эту задачу методом Зойтендейка, начиная поиск из точки . Заметим, что
Первая итерация. Первый шаг. В точке имеем , а множество индексов активных ограничений есть . При этом . Задача нахождения возможного направления имеет вид
минимизировать
при условиях
Можно проверить, решая эту задачу симплекс-методом, что оптимальным решением этой задачи является вектор и .
Второй шаг. Линейный поиск. Любая точка по направлению из точки может быть представлена в виде , а соответствующее ей значение целевой функции равно . Максимальное значение , для которого точка остается допустимой, равно . Итак, решаем задачу одномерной минимизации:
минимизировать
при условии
Оптимальное значение . Итак, .
Вторая итерация. Первый шаг. В точке имеем . Активных ограничений в этой точке нет, поэтому задача определения направления спуска имеет вид:
минимизировать z
при условиях
Оптимальным решением является вектор , а .
Второй шаг. Легко проверить, что , при котором точка допустима, равна 0.3472. При этом активным становится ограничение . Оптимальное значение находим в результате решения задачи:
минимизировать z
при условии
Оно равно 0.3472, так что . Остальные итерации проводятся аналогично. Результаты вычислений на первых четырех итерациях метода приведены в табл. 1.
Таблица 1
| | | | Поиск направления Линейный поиск | |||||
| | | | | | | |||
| 1 | 0.00;–0.75 | -3.375 | -5.50;–3.00 | 1.000;–1.000 | -1.000 | 0.4140 | 0.2088 | 0.2083;–0.5417 |
| 2 | 0.208;–0.541 | -3.635 | -4.25;–4.25 | 1.000;–1.000 | -8.5 | 0.3472 | 0.3472 | 0.555;–0.889 |
| 3 | 0.555;–0.889 | -6.346 | -3.556;–3.555 | 1.000;–0.533 | -1.663 | 0.0924 | 0.0924 | 0.648;–0.840 |
| 4 | 0.648;–0.840 | -6.468 | -3.088;–3.937 | -0.517; 1.000 | -2.340 | 0.0343 | 0.0343 | 0.630;–0.874 |
На рис. 3 показан процесс поиска оптимума. Заметим, что следующей точкой будет , а значение целевой функции в этой точке равно –6.544, тогда как в оптимальной точке значение ц.ф. равно –6.559.
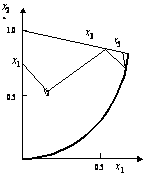
Рисунок 3
Метод возможных направлений может быть модифицирован на случай, когда кроме ограничений неравенств имеются нелинейные ограничения-равенства. Для иллюстрации обратимся к рис. 4, который отвечает единственному ограничению-равенству. Для заданной допустимой точки в этом случае не существует ненулевого направления такого, что при , для некоторого . Это затруднение можно преодолеть, если двигаться вдоль касательного направления , для которого , а затем скорректировать это движение и вернуться в допустимую область (рис. 4).
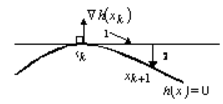
Рисунок 4
Поясним этот подход на примере:
минимизировать (26)
при условиях
,
. (27)
Пусть – допустимая точка и . Будем решать следующую задачу ЛП:
минимизировать (28)
при условиях
, (29)
. (30)
Искомое направление является касательным к ограничениям-равенствам и к некоторым активным нелинейным ограничениям-неравенствам. Линейный поиск вдоль и последующее возвращение в допустимую область приводят в точку , после чего процесс поиска повторяется. Один из существенных недостатков рассмотренного варианта метода состоит в том, что если точка , которая задает текущее решение, окажется близка к границе, определяемой одним из ограничений, а оно не используется в процессе нахождения направления движения, то может оказаться, что сделав лишь небольшой шаг, мы окажемся на границе, определяемой этим ограничением. Поэтому оказывается целесообразным расширить множество активных ограничений , определив его так:
, где – достаточно малое число6.
5. Модификация метода возможных направлений
Анализ алгоритма Зойтендейка показал, что он может не сходиться к точке Куна-Таккера. Трудность здесь заключается в том, что длина шагов вдоль генерируемых направлений стремится к нулю, вызывая «заедание» процесса в неоптимальной точке. Во избежание этого Топкинс и Кейнотт разработали модификацию метода возможных направлений. Эта модификация гарантирует сходимость алгоритма к точке Куна-Таккера. Итак, рассмотрим задачу
7:
минимизировать
при условиях .
При заданной допустимой точке возможное направление находят, решая следующую задачу ЛП:
минимизировать (31)
при условиях
, (32)
, (33)
. (34)
Как видим, в этой модификации при определении направления движения учитываются все ограничения как активные, так и неактивные.
В отличие от метода возможных направлений, описанного выше, здесь мы не сталкиваемся с неожиданным изменением направления, когда приближаемся к границе множества допустимых решений, определяемой неактивным в текущей точке ограничением.
Дадим описание модифицированного алгоритма возможных направлений8:
Начальный этап. Выбрать начальную точку , для которой при . Положить и перейти к основному этапу.
Основной этап. Первый шаг. Положить равным оптимальному решению задачи ЛП:
минимизировать (35)
при условиях , (36)
. (38)
Если , то остановиться, является точкой Куна-Таккера. В противном случае (при ) перейти ко второму шагу.
Второй шаг. Положить равным оптимальному решению задачи:
минимизировать (39)
при условии ,
где
Положить , заменить на и перейти к первому шагу.
Пример 5. Рассмотрим задачу:
минимизировать
при условиях

Применим для решения модифицированный алгоритм возможных направлений. Выберем в качестве начальной точки . Заметим, что в этой точке , а градиенты функций-ограничений соответственно равны .
Первая итерация. Первый шаг.
В точке
имеем . Задача поиска направления спуска имеет вид:
минимизировать
при условиях

В правой части ограничений этой задачи, кроме первого, стоят значения . Заметим, что одно из ограничений ( ) повторяется дважды, следовательно, одно из ограничений можно опустить. Оптимальным решением этой задачи является вектор , при котором .
Второй шаг (линейный поиск). Решаем задачу:
минимизировать
Максимальное значение , для которого точка допустима, определяется соотношением (40) и равно . Тогда оптимальным решением задачи (41) будет .
Таким образом, .
Вторая итерация. Первый шаг. В точке имеем . В качестве направления берется оптимальное решение следующей задачи:
минимизировать
при условиях

Оптимальным решением этой задачи является вектор .
Второй шаг. Максимальное значение , для которого точка допустима, равно . Легко можно проверить, что достигает минимума на отрезке в точке . Следовательно, . Далее этот процесс повторяется. В табл. 2 приведены результаты вычислений на первых пяти итерациях.
Таблица 2
| | | | Первый шаг Второй шаг | |||||
| | | | | | | |||
| 1 | 0.00;–0.75 | -3.375 | -5.50;–3.00 | 0.714;-0.0357 | -0.714 | 0.84 | 0.84 | 0.600;–0.720 |
| 2 | 0.600;–0.720 | -5.827 | -3.04; -4.32 | -0.0712; –0.117 | -0.288 | 1.562 | 1.562 | 0.489;–0.902 |
| 3 | 0.489;–0.902 | -6.145 | -3.849;–3.369 | 0.0957;–0.0555 | -0.1816 | 1.564 | 1.564 | 0.6385;–0.8154 |
| 4 | 0.6385;–0.8154 | -6.343 | -5.63 ;–4.02 | -0.016;–0.0433 | -0.0840 | 1419 | 1.419 | 0.616;– 0.877 |
| 5 | 0.616;–0.877 | -6.508 | -3.29;–3.725 | 0.0268;–0.0132 | -0.0303 | 1.455 | 1.455 | 0.655;–0.858 |
Траектория движения точки, задающей текущее решение, показана на рис. 5. В конце пятой итерации получена точка со значением целевой функции –6.559. Заметим, что в оптимальной точке значение целевой функции равно –6.613.
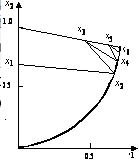
Рисунок 5
Заключение
Методы возможных направлений – наиболее исследованный класс методов выпуклого программирования (задачи выпуклого программирования – это такие задачи нелинейного программирования, в которых целевые функции и функции ограничений выпуклы).
Идея метода возможных направлений заключается в том, что в каждой очередной точке находится направление спуска такое, что перемещение точки по этому направлению на некоторое расстояние не приводит к нарушению ограничений задачи. Таким образом, метод возможных направлений можно рассматривать как естественное распространение метода градиентного спуска на задачи минимизации с ограничениями.
В отличие от других численных методов решения таких задач, метод возможных направлений обладает тем преимуществом, что для отыскания направления спуска достаточно решить задачу линейного программирования с небольшим числом ограничений.
Список использованных источников
-
Аттетков А.В., Галкин С.В., Зарубин В.С. Методы оптимизации: Учеб. для вузов / Под ред. B.C. Зарубина, А. П. Крищенко. - М.: МГТУ им. Н. Э. Баумана, 2003. - 440 с. -
Зойтендейк Г. Методы возможных направлений. - М.: ИЛ, 1963. – 175 с. -
Методы возможных направлений [Электронный ресурс]. – Режим доступа: http://iasa.org.ua/lections/iso/6/6.5.htm. -
Методы математического программирования в задачах оптимизации сложных технических систем: учебное пособие / А.М. Загребаев, Н.А. Крицына, Ю.П. Кулябичев, Ю.Ю. Шумилов. – М.: МИФИ, 2007. – 332 с. -
Нурминский Е.А. Методы оптимизации: Курс лекций [Электронный ресурс]. – Режим доступа: http://elis.dvo.ru/nurmi/edu/optimization.pdf.
1 Зойтендейк Г. Методы возможных направлений. - М.: ИЛ, 1963. – 175 с.
2 Методы математического программирования в задачах оптимизации сложных технических систем: учебное пособие / А.М. Загребаев, Н.А. Крицына, Ю.П. Кулябичев, Ю.Ю. Шумилов. – М.: МИФИ, 2007. С. 226-228.
3 Аттетков А.В., Галкин С.В., Зарубин В.С. Методы оптимизации: Учеб. для вузов / Под ред. B.C. Зарубина, А. П. Крищенко. - М.: МГТУ им. Н. Э. Баумана, 2003. С. 387-389.


