В таблице h-функций находим соответствующую каждому    функцию 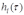  . Искомую составляющую    получаем из этой функции путём умножения ординат    на величину 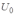  . Время    получаем как частное от деления величины    на   .   ;   .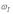

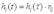Таблица 1.4.3 — Значения для построения переходного процесса.

 

t табл,	h табл,	t	h1(t)	t табл,	h табл,	t	h2(t)	t табл,	h табл,	t	h2(t)
0	0,0000	0,0000	0,0000	0	0,0000	0,0000	0,0000	0	0,0000	0,0000	0,0000
0,5	0,1760	0,0200	1,1733	0,5	0,2400	0,0100	-0,2704	0,5	0,2400	0,0050	-0,1296
1	0,3400	0,0400	2,2667	1	0,4610	0,0200	-0,5194	1	0,4610	0,0100	-0,2489
1,5	0,4940	0,0600	3,2933	1,5	0,6650	0,0300	-0,7492	1,5	0,6650	0,0150	-0,3591
2	0,6280	0,0800	4,1867	2	0,8330	0,0400	-0,9385	2	0,8330	0,0200	-0,4498
2,5	0,7390	0,1000	4,9267	2,5	0,9670	0,0500	-1,0895	2,5	0,9670	0,0250	-0,5222
3	0,8280	0,1200	5,5200	3	1,0610	0,0600	-1,1954	3	1,0610	0,0300	-0,5729
3,5	0,8920	0,1400	5,9467	3,5	1,1150	0,0700	-1,2562	3,5	1,1150	0,0350	-0,6021
4	0,9380	0,1600	6,2533	4	1,1420	0,0800	-1,2867	4	1,1420	0,0400	-0,6167
4,5	0,9600	0,1800	6,4000	4,5	1,1380	0,0900	-1,2821	4,5	1,1380	0,0450	-0,6145
5	0,9770	0,2000	6,5133	5	1,1170	0,1000	-1,2585	5	1,1170	0,0500	-0,6032
5,5	0,9860	0,2200	6,5733	5,5	1,0920	0,1100	-1,2303	5,5	1,0920	0,0550	-0,5897
6	0,9820	0,2400	6,5467	6	1,0510	0,1200	-1,1841	6	1,0510	0,0600	-0,5675
6,5	0,9800	0,2600	6,5333	6,5	1,0180	0,1300	-1,1469	6,5	1,0180	0,0650	-0,5497
7	0,9790	0,2800	6,5267	7	0,9930	0,1400	-1,1188	7	0,9930	0,0700	-0,5362
7,5	0,9800	0,3000	6,5333	7,5	0,9740	0,1500	-1,0974	7,5	0,9740	0,0750	-0,5260
8	0,9850	0,3200	6,5667	8	0,9660	0,1600	-1,0884	8	0,9660	0,0800	-0,5216
8,5	0,9890	0,3400	6,5933	8,5	0,9660	0,1700	-1,0884	8,5	0,9660	0,0850	-0,5216
9	0,9970	0,3600	6,6467	9	0,9700	0,1800	-1,0929	9	0,9700	0,0900	-0,5238
9,5	1,0040	0,3800	6,6933	9,5	0,9750	0,1900	-1,0985	9,5	0,9750	0,0950	-0,5265
10	1,0090	0,4000	6,7267	10	0,9820	0,2000	-1,1064	10	0,9820	0,1000	-0,5303
10,5	1,0130	0,4200	6,7533	10,5	0,9870	0,2100	-1,1120	10,5	0,9870	0,1050	-0,5330
11	1,0150	0,4400	6,7667	11	0,9970	0,2200	-1,1233	11	0,9970	0,1100	-0,5384
11,5	1,0160	0,4600	6,7733	11,5	0,9970	0,2300	-1,1233	11,5	0,9970	0,1150	-0,5384
12	1,0150	0,4800	6,7667	12	0,9970	0,2400	-1,1233	12	0,9970	0,1200	-0,5384
12,5	1,0130	0,5000	6,7533	12,5	0,9970	0,2500	-1,1233	12,5	0,9970	0,1250	-0,5384
13	1,0120	0,5200	6,7467	13	0,9970	0,2600	-1,1233	13	0,9970	0,1300	-0,5384
13,5	1,0110	0,5400	6,7400	13,5	0,9980	0,2700	-1,1244	13,5	0,9980	0,1350	-0,5389
14	1,0110	0,5600	6,7400	14	1,0000	0,2800	-1,1267	14	1,0000	0,1400	-0,5400
14,5	1,0120	0,5800	6,7467	14,5	1,0020	0,2900	-1,1289	14,5	1,0020	0,1450	-0,5411
15	1,0120	0,6000	6,7467	15	1,0050	0,3000	-1,1323	15	1,0050	0,1500	-0,5427
15,5	1,0140	0,6200	6,7600	15,5	1,0080	0,3100	-1,1357	15,5	1,0080	0,1550	-0,5443
16	1,0150	0,6400	6,7667	16	1,0110	0,3200	-1,1391	16	1,0110	0,1600	-0,5459
16,5	1,0160	0,6600	6,7733	16,5	1,0110	0,3300	-1,1391	16,5	1,0110	0,1650	-0,5459
17	1,0160	0,6800	6,7733	17	1,0120	0,3400	-1,1402	17	1,0120	0,1700	-0,5465
17,5	1,0150	0,7000	6,7667	17,5	1,0090	0,3500	-1,1368	17,5	1,0090	0,1750	-0,5449
18	1,0150	0,7200	6,7667	18	1,0080	0,3600	-1,1357	18	1,0080	0,1800	-0,5443
18,5	1,0150	0,7400	6,7667	18,5	1,0060	0,3700	-1,1334	18,5	1,0060	0,1850	-0,5432
19	1,0150	0,7600	6,7667	19	1,0010	0,3800	-1,1278	19	1,0010	0,1900	-0,5405
19,5	1,0140	0,7800	6,7600	19,5	0,9980	0,3900	-1,1244	19,5	0,9980	0,1950	-0,5389
20	1,0130	0,8000	6,7533	20	0,9960	0,4000	-1,1222	20	0,9960	0,2000	-0,5378
20,5	1,0120	0,8200	6,7467	20,5	0,9950	0,4100	-1,1210	20,5	0,9950	0,2050	-0,5373
21	1,0110	0,8400	6,7400	21	0,9950	0,4200	-1,1210	21	0,9950	0,2100	-0,5373
21,5	1,0110	0,8600	6,7400	21,5	0,9960	0,4300	-1,1222	21,5	0,9960	0,2150	-0,5378
22	1,0110	0,8800	6,7400	22	0,9960	0,4400	-1,1222	22	0,9960	0,2200	-0,5378
22,5	1,0110	0,9000	6,7400	22,5	0,9970	0,4500	-1,1233	22,5	0,9970	0,2250	-0,5384
23	1,0110	0,9200	6,7400	23	0,9980	0,4600	-1,1244	23	0,9980	0,2300	-0,5389
23,5	1,0100	0,9400	6,7333	23,5	0,9990	0,4700	-1,1255	23,5	0,9990	0,2350	-0,5395
24	1,0100	0,9600	6,7333	24	1,0000	0,4800	-1,1267	24	1,0000	0,2400	-0,5400
24,5	1,0090	0,9800	6,7267	24,5	1,0000	0,4900	-1,1267	24,5	1,0000	0,2450	-0,5400
25	1,0080	1,0000	6,7200	25	1,0000	0,5000	-1,1267	25	1,0000	0,2500	-0,5400
25,5	1,0080	1,0200	6,7200	25,5	1,0000	0,5100	-1,1267	25,5	1,0000	0,2550	-0,5400
26	1,0070	1,0400	6,7133	26	1,0000	0,5200	-1,1267	26	1,0000	0,2600	-0,5400

---

При помощи функции линейной интерполяции linterp, встроенной в математический пакет MathCAD, находим функции переходных характеристик, соответствующих каждой из трапеций, и производим их сложение.


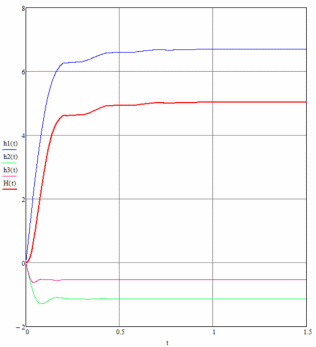
Рисунок 1.4.4 — Графики переходных процессов замкнутой САУ:

h1(t) — переходная характеристика первой трапеции;

h2(t) — переходная характеристика второй трапеции;

h3(t) — переходная характеристика третьей трапеции;

H(t) — суммарная переходная характеристика.

---

Определение параметров и построение желаемой ЛАЧХ

Параметры для построения исходной ЛАЧХ.

 



 

T1 = 0.02с

T2 = 0.04с

T3 = 0.12с

ω1 = 50 с^-1

ω2 = 25 с^-1

ω3 = 8.333 с^-1

20·log K = 20·log 1 = 0 дБ

Переходный процесс должен удовлетворять следующим показателям качества:

 ≤0,15с,   ≤30%.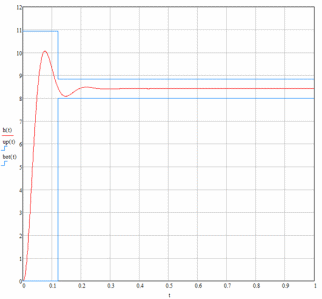



Рисунок 1.7.1 Переходный процесс скорректированной САУ

Анализируя переходной процесс системы управления (рисунок 1.7.1), можем сказать, что время регулирования и перерегулирование, не выходит за пределы значений, заданных „коробочкой Солодовникова“. Следовательно, переходный процесс удовлетворяет предъявленным условиям качества регулирования САУ.

1.8 Анализ устойчивости скорректированной САУ

Производится по критерию устойчивости Михайлова.

Передаточная функция разомкнутой скорректированной САУ имеет вид:

 



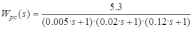
Передаточная функция замкнутой скорректированной САУ определяется следующим образом:

 





 

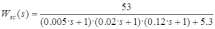
Раскроем скобки в знаменателе передаточной функции:



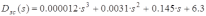
Заменяем переменную s на jω:



Разобьем это выражение на действительную и мнимую составляющие.

 — вещественная часть;

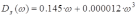 — мнимая часть.

По этим данным строится годограф Михайлова. Для устойчивости САУ, необходимо и достаточно, чтобы вектор годографа Михайлова последовательно обошёл вокруг начало координат и в 3 квадранте ушёл в бесконечность.

ω ∈ (0 ÷ 300)

---

Рисунок 1.8.1 — Годограф Михайлова для скорректированной системы

Таблица 1.8.1 — Данные для построения годографа Михайлова

ω	0	10	30	50	60	70	80	100	200	500
Cз(ω)	6.3	6.00	3.52	-1.44	-4.85	-8.88	-13.5	-24.7	-117.7	-768.7
Dз(ω)	0	1.438	4.03	5.75	6.108	6.03	5.46	2.5	-67	-1427

 

Вектор Михайлова обошел вокруг начала координат и в 3 квадранте ушел в бесконечность. Отсюда следует, что скорректированная САУ устойчива.

Исследование нелинейной системы.

Согласно заданию, структурная схема нелинейной САУ выглядит следующим образом:



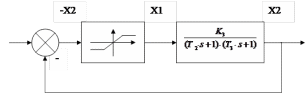
Рисунок 2.1 – структурная схема нелинейной системы.

 


Рисунок 2.2 – передаточная характеристика нелинейного звена:

с = 2;

b = c/K₄ = 2/0.1 = 5.

 

Построение фазового портрета нелинейной САУ

Выполняется вручную методом изоклин при помощи математического пакета MathCAD, в котором производится построение изоклин..

Уравнения изоклин получаем исходя сначала из передаточной функции линейной части системы:




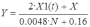
Здесь, N – коэффициент угла наклона фазовой

---

траектории при прохождении через изоклину;

X – отклонение выходной величины от её заданного значения;

X₁(t) – функция, зависящая от свойств нелинейного звена.

X₁(t) принимает следующие значения:

    b при X < –c

    –b при X > c

    K4∙X при –c≤X≤c.



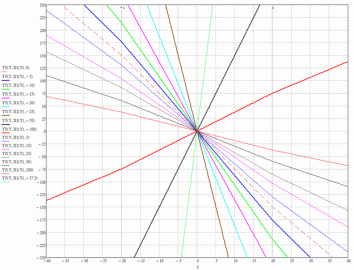
Рисунок 2.1.1 — Изоклины фазового портрета.

 

Талица 2.1.1 — Данные для построения изоклин.

C	-100				-50				-37.5				-25
X	-40	-20	20	40	-40	-20	20	40	-40	-20	20	40		-40	-20	20	40
Y	-137.5	-75	75	137.5	-550	-300	300	550	-2200	-1200	1200	2200		1100	600	-600	-1100
C	-20				-15				-10				-5
X	-40	-20	20	40	-40	-20	20	40	-40	-20	20	40		-40	-20	20	40
Y	687.5	375	-375	-687.5	500	272.7	-272.7	-500	392.9	214.3	-214.3	-392.9		323.5	176.5	-176.5	-323.5
C	0				5				10				15
X	-40	-20	20	40	-40	-20	20	40	-40	-20	20	40		-40	-20	20	40
Y	275	150	-150	-275	239.1	130.4	-130.4	-239.1	211.5	115.4	-115.4	-211.5		189.7	103.4	-103.4	-189.7
C	20				25				50				100
X	-40	-20	20	40	-40	-20	20	40	-40	-20	20	40		-40	-20	20	40
Y	171.9	93.8	-93.8	-171.9	157.1	85.7	-85.7	-157.1	110	60	-60	-110		68.8	37.5	-37.5	-68.8

---

Смотрите также файлы

• Карточки по чтению 1 класс (любой умк).docx

• Министерство трпорта российской федерации.docx

• создание и использование формул.doc

• Занятие 1 Экскурсия по школе Орг момент. Давайте знакомиться. Когда знаешь, с кем держишь путь, идти веселее.docx

• Новогодний праздник в 1м классе.doc