Проверяемые задания

Алгоритм выбора студентом своего варианта

При решении задач введены обозначения:

• 
  С – количество букв в имени;
  
• 
  П – количество букв в фамилии (если больше девяти, то берется последняя цифра);
  
• 
  Г – количество букв в отчестве;
  
• 
  ПСГ – это вариант.
  

ПСГ= 8 5 12

1. Записать данные задания.

Круглая пластина радиуса R = 3,9 (м) и массой m₁ = 35 (кг) вращается с угловой скоростью -15 (с^-1) вокруг вертикальной оси z, проходящей через точку О перпендикулярно рис. 1.

На пластине имеется желоб, по которому начинает двигаться точка М массой m₂ = 10 (кг) по закону / АМ / = 1,5t² (м).

Найти угловую скорость пластины в момент времени 1 с.
2. Отобразить рисунок, на котором показаны все силы и скорости.



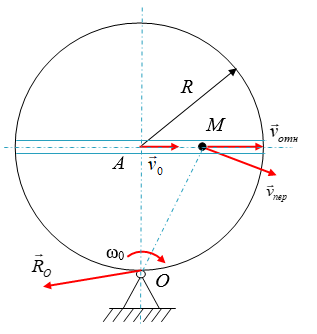
Силы тяжести, действующие на пластину и материальную точку будут перпендикулярны плоскости пластины. Так как в начальный момент времени угловая скорость пластины отрицательна, то вращение пластины будет происходить по часовой стрелке.

3. Записать уравнение теоремы об изменении кинетического момента механической системы.

Рассмотрим механическую систему, состоящую из пластины и материальной точки М. Для определения применим теорему об изменении кинетического момента системы относительно оси z: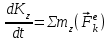

.

На систему действуют внешние силы: силы тяжести пластины и материальной точки, реакция опоры 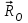. Т.к. силы тяжести параллельны оси z, , реакция опоры 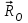пересекает ее, то их моменты относительно этой оси равны нулю. Тогда и .

4. Решить уравнение.

Умножая обе части этого уравнения на

---

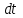
и интегрируя, получим:



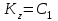
Или

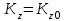(1)

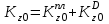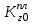Для рассматриваемой механической системы в начальный момент времени , где и 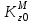– кинетические моменты пластины и точки соответственно.

Пластина вращается вокруг оси z, следовательно 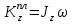. По теореме Гюйгенса 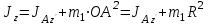( 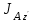– момент инерции относительно оси параллельной оси z и проходящей через центр А пластины). Но 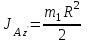. Тогда

.

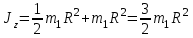Следовательно, .

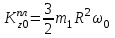В начальный момент времени точка М находится в центре пластины и ее скорость:



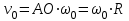
И ее начальный кинетический момент: .

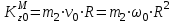Следовательно, начальный кинетический момент системы:



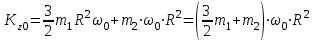
В момент времени t=1c кинетический момент пластины:



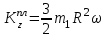
Для определения 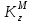рассмотрим движение точки М как сложное, считая его движение по пластине относительным, а вращение самой пластины – переносным движением. Тогда .

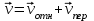Т.к. , то .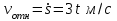

При t=1c ; .

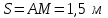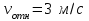И вектор направлен так, как показано на рис.2

Тогда

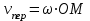
И вектор

---

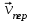
направлен перпендикулярно ОМ
Из треугольника OАМ получим:



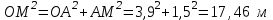
И кинетический момент точки равен



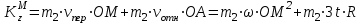
И кинетический момент рассматриваемой системы при t=1c:



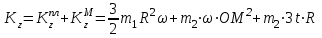
Уравнение (1) примет вид:



Или



Подставив исходные данные, получим:



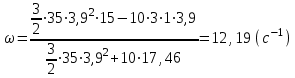
5. Записать ответ.

---

Смотрите также файлы

• Игнатьев Андрей, 137ос1 Владелец магазина беспошлинной торговли.docx

• Прогнозирование и планирование социального развития и уровня жизни населения.docx

• Современные проблемы молодой семьи.doc

• Алина Кабаева.docx

• Семинар 2 Римское царство. Римское царство характеризуется следующими временными рамками (753510 гг до н э.).docx