ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.04.2024
Просмотров: 17
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, так как open→n∣∣=√A2+B2=√(−12)2+(√32)=1n→=A2+B2=-122+32=1 и C=−3≤0C=-3≤0 .
Уравнение задает в декартовой системе координат 0ху прямую линию, нормальный вектор которой имеет координаты (−12, √32)-12, 32 . Линия удалена от начала координат на 33 единицы в направлении нормального вектора →n=(−12, √32)n→=-12, 32 .
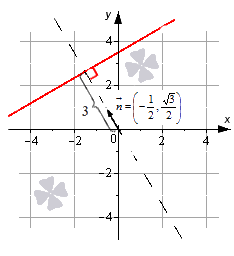
Обращаем ваше внимание на то, что нормальное уравнение прямой на плоскости позволяет находить расстояние от точки до прямой на плоскости.
Если в общем уравнении прямой Ax+By+C=0Ax+By+C=0 числа А, ВА, В и СС таковы, что уравнение Ax+By+C=0Ax+By+C=0 не является нормальным уравнением прямой, то его можно привести к нормальному виду. Подробнее об этом читайте в статье «Нормальное уравнение прямой».
Уравнение задает в декартовой системе координат 0ху прямую линию, нормальный вектор которой имеет координаты (−12, √32)-12, 32 . Линия удалена от начала координат на 33 единицы в направлении нормального вектора →n=(−12, √32)n→=-12, 32 .

Обращаем ваше внимание на то, что нормальное уравнение прямой на плоскости позволяет находить расстояние от точки до прямой на плоскости.
Если в общем уравнении прямой Ax+By+C=0Ax+By+C=0 числа А, ВА, В и СС таковы, что уравнение Ax+By+C=0Ax+By+C=0 не является нормальным уравнением прямой, то его можно привести к нормальному виду. Подробнее об этом читайте в статье «Нормальное уравнение прямой».

