Файл: Лабораторная работа 1 Моделирование на эвм дискретных и квантованных сигналов.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.04.2024
Просмотров: 20
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
могут иметь фильтры с разным шагом дискретизации, но для разных частот .
Генератор случайных чисел пакета MathCAD генерирует числа с равномерным распределением от 0 до некоторого заданного числа a. Для получения симметричного распределения относительно нуля нужно сместить все выборки случайного сигнала на a/2 вниз.
3. Порядок выполнения работы.
1. Познакомиться с пакетом прикладных программ MathCAD, пользуясь системой помощи.
2. Пользуясь операторами и функциями системы MathCAD разработать алгоритм, моделирующий дискретный аналог меандра для 4-6 периодов. Число единичных (и нулевых) отсчетов взять от 5 до 8.
Построить график дискретного аналога меандра.
3. Используя тригонометрические функции разработать алгоритм, моделирующий дискретный аналог гармонического колебания для 3-4 периодов. Шаг дискретизации по фазе взять равным 10, 30, 45, 90 и 120 градусов. Для каждого шага дискретизации построить график.
Шаг дискретизации по фазе взять равным 10, 30, 45, 90 и 120 градусов. Для каждого шага дискретизации построить график.
4. Используя программу генерирования случайных чисел смоделировать отсчеты случайного процесса с равномерным распределением в амплитудном диапазоне -1≤n(k)≥1.Число отсчетов взять равным от 50 до 100.
5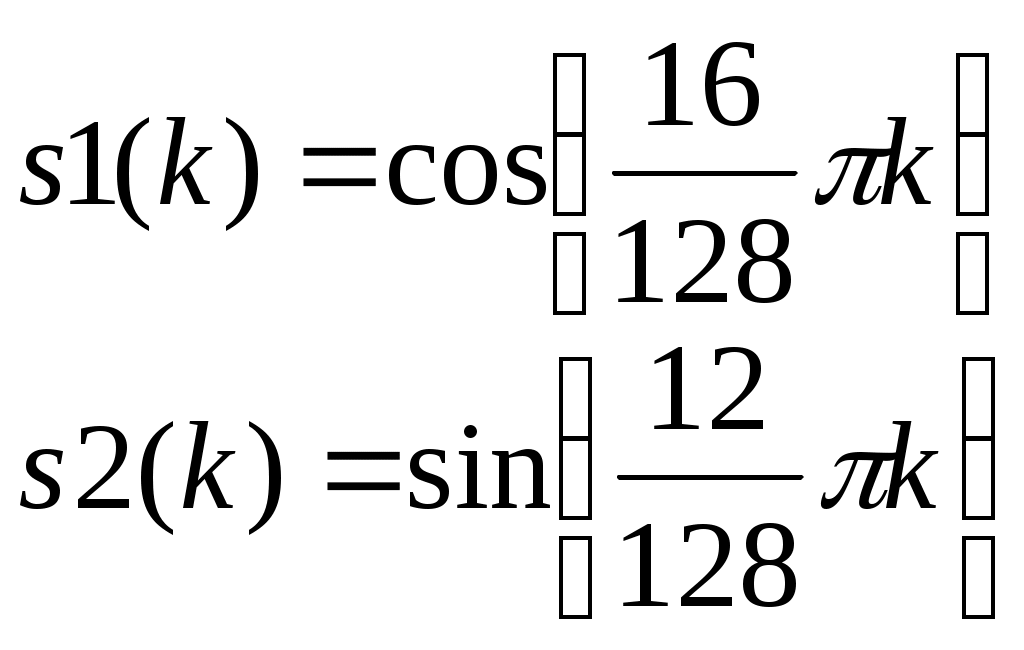
. Смоделировать отсчеты аддитивной смеси двух гармонических сигналов и шума для отношения с/ш = от 1 до 5 по напряжению для 128 отсчетов. Гармонические дискретные сигналы заданы выражениями
где k - номер отсчета
Построить графики сигнала, шума, смеси сигнала с шумом.
6. Распечатать графики дискретных аналогов меандра, дискретной гармонической последовательности для различных фазовых углов дискретизации, дискретной последовательности отсчетов сигнала, шума и смеси сигнал + шум.
7. Индивидуальное задание по построению дискретных аналогов сигналов выдается персонально для каждого студента преподавателем после выполнения общей части лабораторной работы.
4. Содержание отчета.
Отчет должен содержать распечатки программ моделирования испытательных сигналов и графики моделей дискретных сигналов, рассмотренных в пп.3.2 - 3.5.
5. Контрольные вопросы.
1.Какой сигнал называется меандром?
2.Какой сигнал называется детерминированным?
3.Какой сигнал называется случайным?
4.Какой сигнал называется дискретной гармонической последовательностью?
5.Почему удобнее задавать шаг дискретизации через фазовый угол?
6.О чем говорит теорема Котельникова?
7.В какую сторону нужно изменить фазовый угол дискретизации, чтобы увеличить или уменьшить частоту сигнала при неизменном временном шаге дискретизации?
ЛИТЕРАТУРА
1.Гоноровский И.С. Радиотехнические цепи и сигналы.
2.Конспект лекций по курсу "Теоретические основы информационной техники".
ЛАБОРАТОРНАЯ РАБОТА № 2
Вычисление спектра сигналов на ЭВМ с помощью БПФ
Научиться находить спектр сигнала с помощью БПФ и по известному спектру находить исходный сигнал с помощью обратного БПФ
В линейном пространстве сигналов можно выделить специальное подмножество, играющее роль координатных осей. Говорят, что совокупность векторов {е1 е2, е3, ...}, принадлежащих множеству М, является линейно независимой, если равенство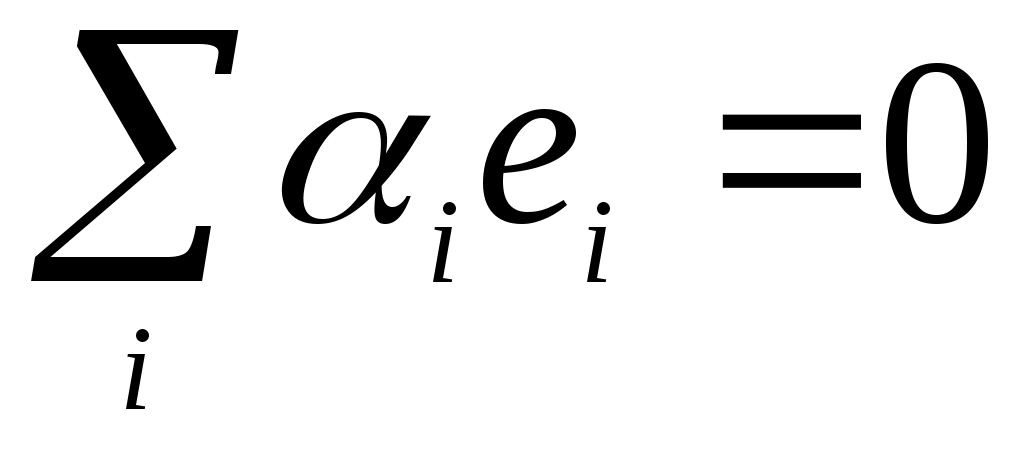 возможно лишь в случае одновременного обращения в нуль всех числовых коэффициентов αi.
возможно лишь в случае одновременного обращения в нуль всех числовых коэффициентов αi.
Система линейно независимых векторов образует координатный базис в линейном пространстве. Если дано разложение некоторого сигнала s(t) в виде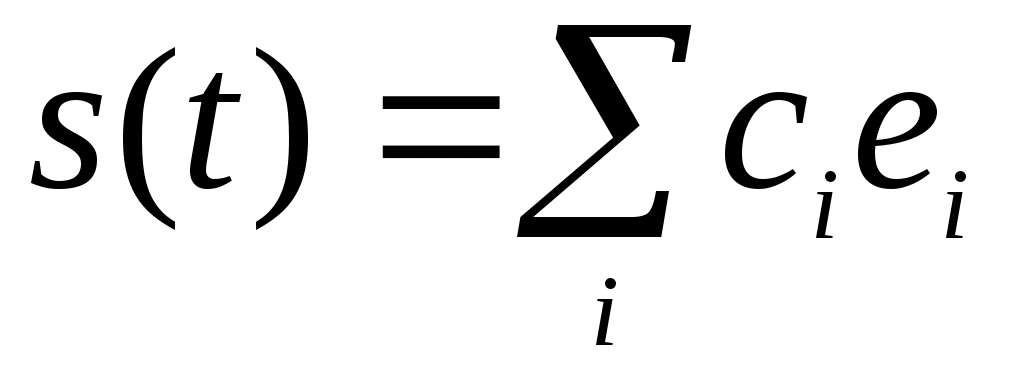 то числа {с1 с2, с3, ...} являются проекциями сигнала s(t) относительно выбранного базиса.
то числа {с1 с2, с3, ...} являются проекциями сигнала s(t) относительно выбранного базиса.
Длину вектора в математике называют его нормой. Линейное пространство сигналов L является нормированным, если каждому вектору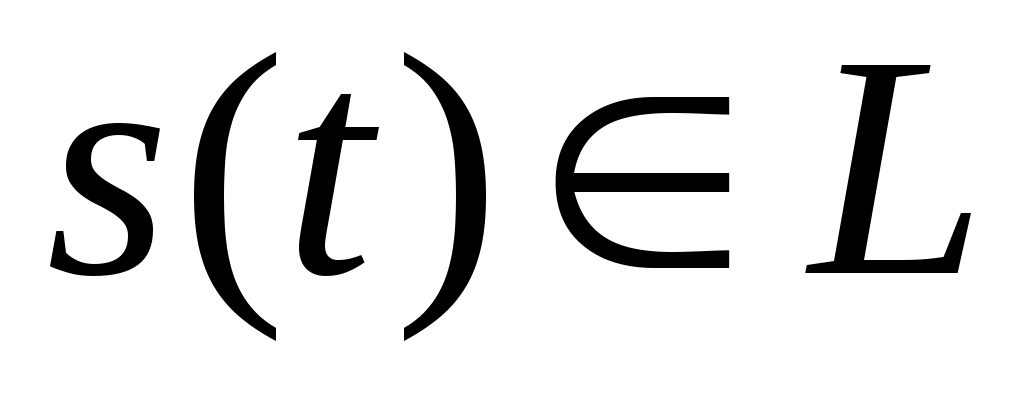 однозначно сопоставлено число
однозначно сопоставлено число — норма этого вектора.
— норма этого вектора.
В радиотехнике чаще всего полагают, что вещественные аналоговые сигналы имеют норму
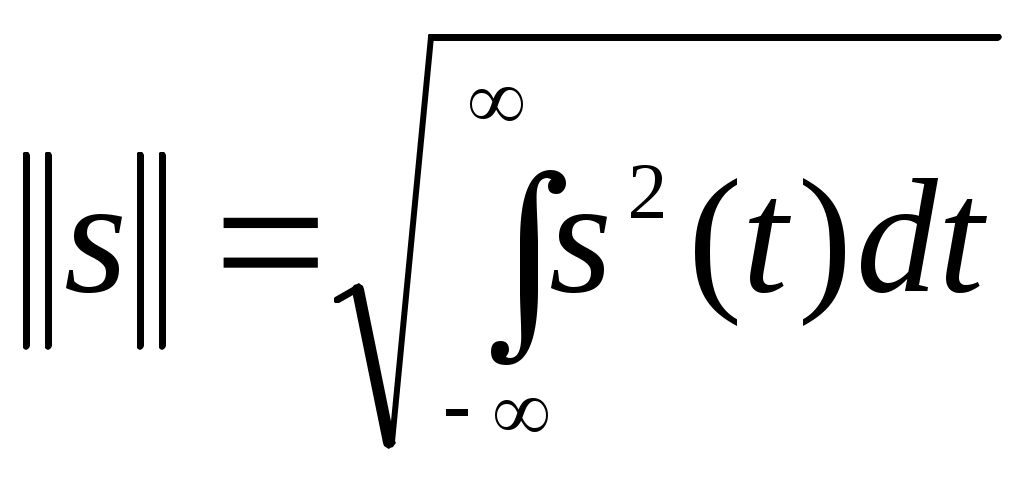 (2.1)
(2.1)
Данная формула в равной мере относится как к аналоговым, так и к дискретным сигналам (из двух возможных значений корня выбирается положительное).
Функция u(t), для которой выполняется условие
 (2.2)
(2.2)
называется нормированной функцией, а система нормированных функций u1(t), u2(t)…, в которой две различные функции взаимно ортогональны, называется ортонормированной системой.
Квадрат нормы носит название энергии сигнала
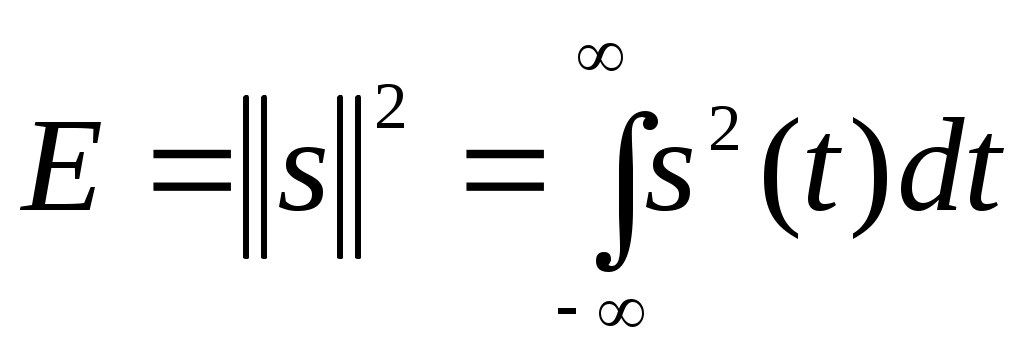 (2.3)
(2.3)
Определять норму сигнала с помощью формулы (2.1) целесообразно по следующим причинам:
1. В радиотехнике о величине сигнала часто судят, исходя из суммарного энергетического эффекта, например количества теплоты, выделяемой в резисторе.
2. Энергетическая норма оказывается «нечувствительной» к изменениям формы сигнала, может быть, и значительным, но происходящим на коротких отрезках времени.
Среди разнообразных систем ортогональных функций, которые могут использоваться в качестве базисов для представления радиотехнических сигналов, исключительное место занимают гармонические (синусоидальные и косинусоидальные) функции.
Математической моделью процесса, повторяющегося во времени, является периодический сигнал s(t) со следующим свойством:
 , где n = 1,2,3… (2.4)
, где n = 1,2,3… (2.4)
Здесь Т — период сигнала.
Два сигнала u и v называются ортогональными, если их скалярное произведение, а значит, и взаимная энергия равны нулю:
 (2.5)
(2.5)
Выражение (2.4) называют принципом ортогональности двух сигналов.
Пусть Н — гильбертово пространство сигналов с конечным значением энергии. Эти сигналы определены на отрезке времени [t1, t2], конечном или бесконечном. Предположим, что на этом же отрезке задана бесконечная система функций {u0, u1, u2, ….un, …}, ортогональных друг другу и обладающих единичными нормами:
 (2.6)
(2.6)
Говорят, что при этом в пространстве сигналов задан ортонормированный базис.
Разложим произвольный сигнал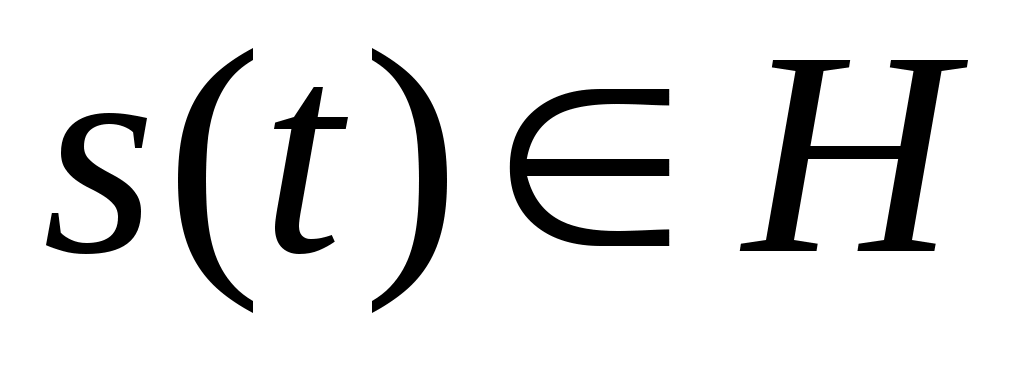
в ряд, согласно следующему выражению
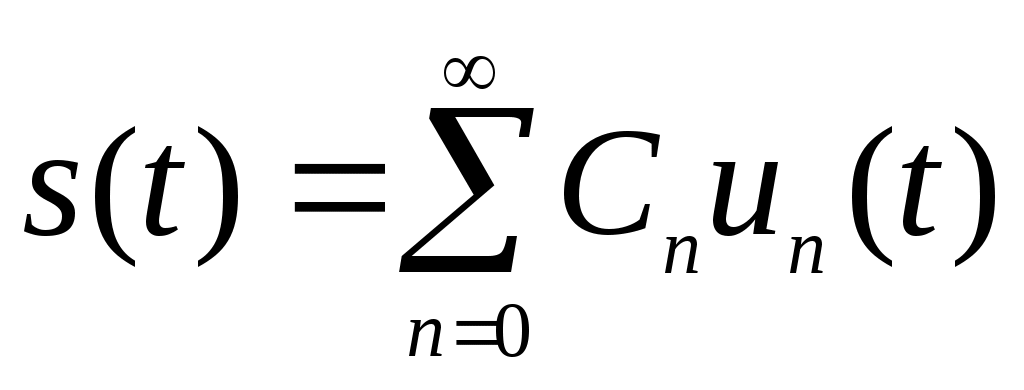 (2.7)
(2.7)
Представление (2.7) называется обобщенным рядом Фурье сигнала s(t) в выбранном базисе. Коэффициенты Cn определяются по формуле:
 (2.8)
(2.8)
Совокупность полученных коэффициентов Cn называют спектром сигнала s(t ) в ортогональной системе u(t) и полностью определяют этот сигнал.
Введем основную частоту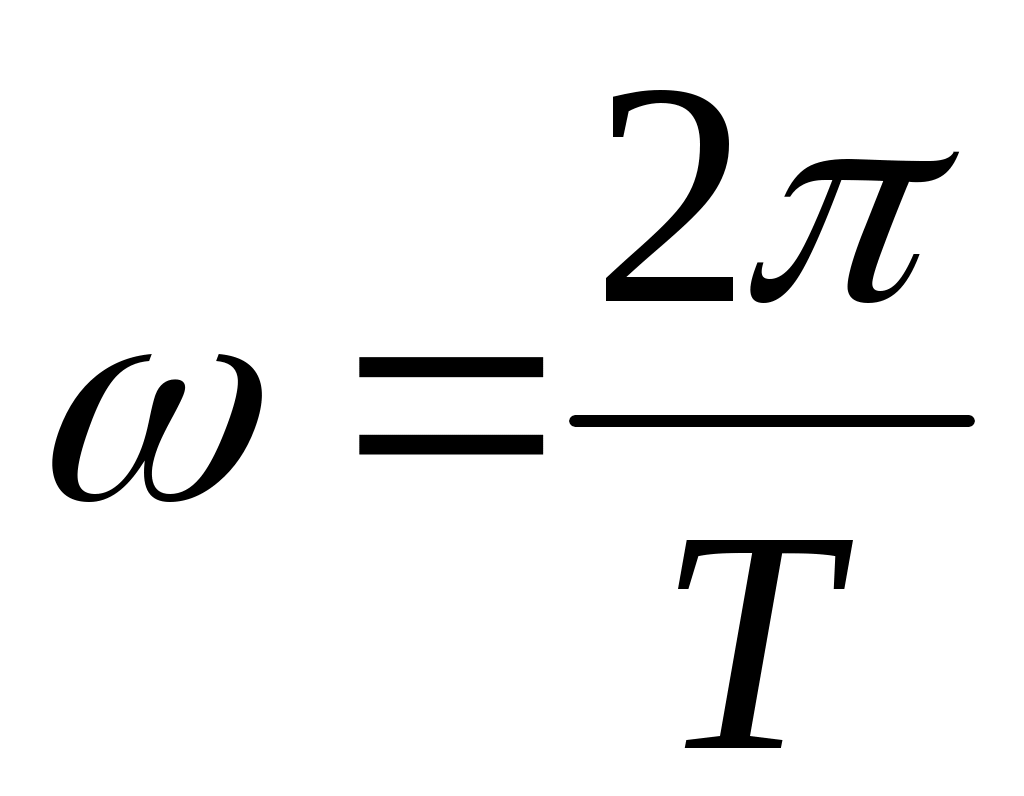 последовательности, образующей периодический сигнал. Вычисляя коэффициенты разложения по формуле (2.8), запишем ряд Фурье для периодического сигнала
последовательности, образующей периодический сигнал. Вычисляя коэффициенты разложения по формуле (2.8), запишем ряд Фурье для периодического сигнала
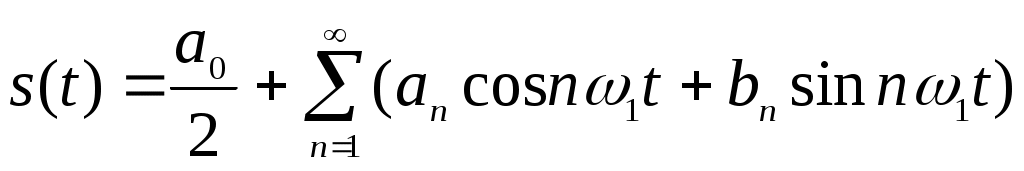 (2.9)
(2.9)
с коэффициентами :

 (2.10)
(2.10)

Итак, в общем случае периодический сигнал содержит не зависящую от времени постоянную составляющую и бесконечный набор гармонических колебаний, так называемых гармоник с частотами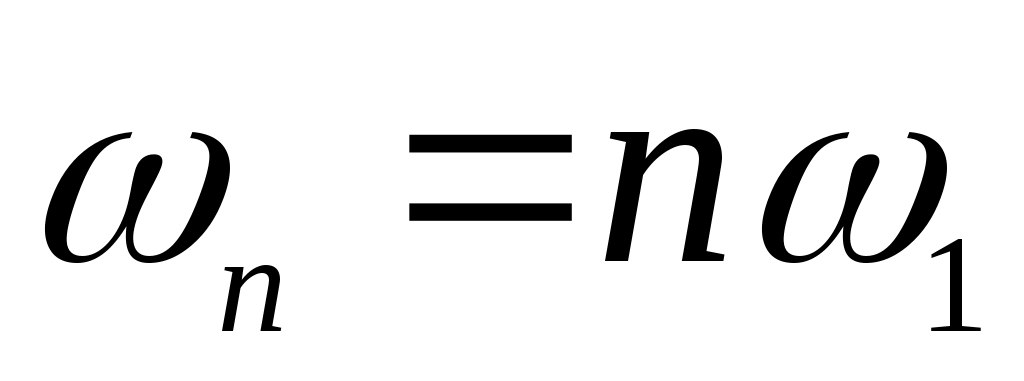 , где (n = 1, 2, 3, ,..), кратными основной частоте последовательности.
, где (n = 1, 2, 3, ,..), кратными основной частоте последовательности.
Каждую гармонику можно описать ее амплитудой Аn начальной фазой φn . Для этого коэффициенты ряда Фурье следует записать в виде:
 ,
, 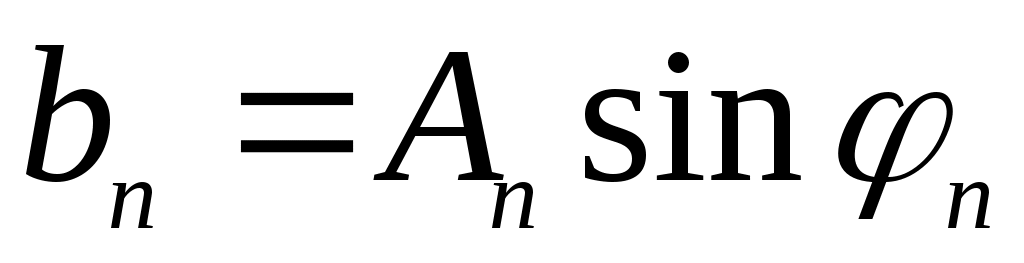
Так что (2.11)
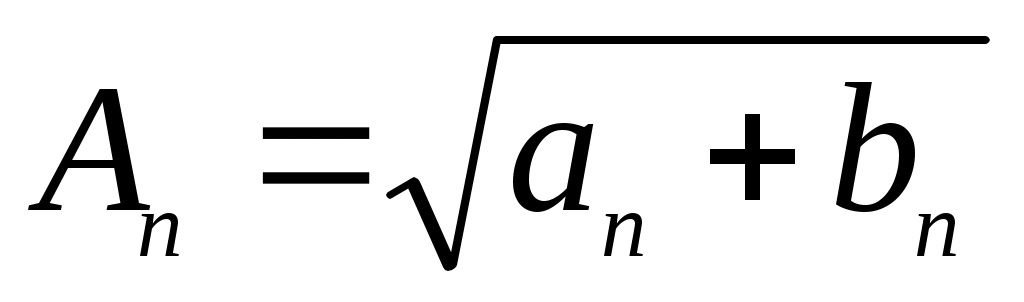 ,
, 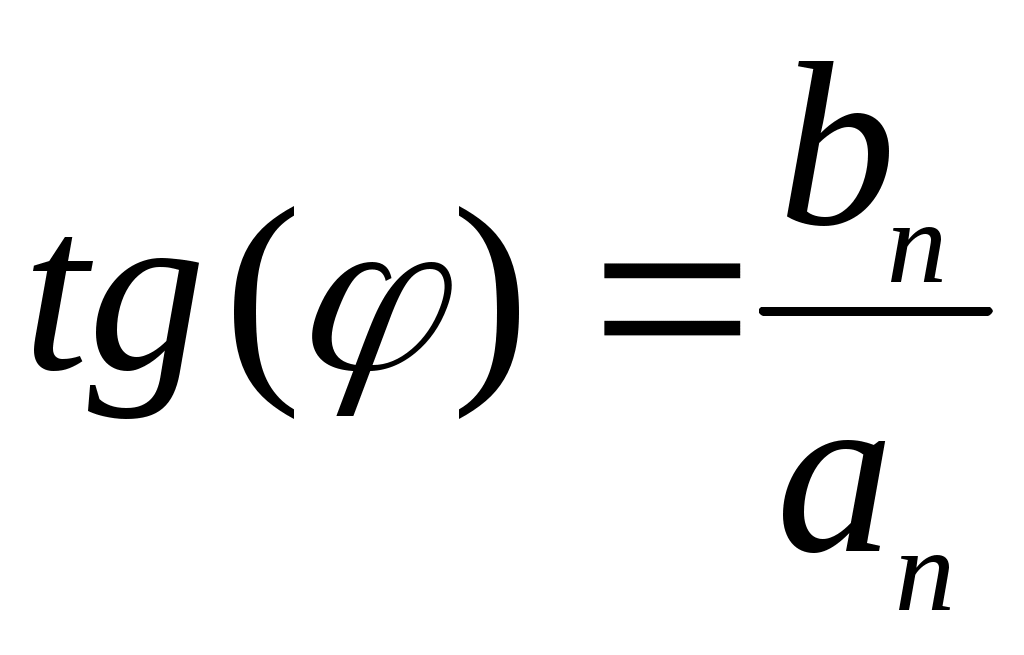
Подставив эти выражения в (2.9), получим другую, эквивалентную форму ряда Фурье:
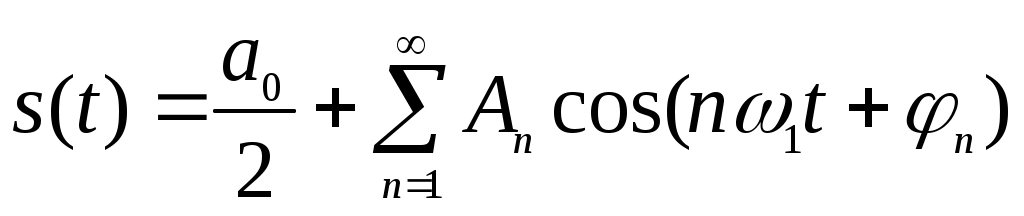
Спектральной диаграммой периодического сигнала принято называть графическое изображение коэффициентов ряда Фурье для конкретного сигнала. Различают амплитудные и фазовые спектральные диаграммы.
Для того, чтобы получить комплексную форму ряда Фурье, необходимо выполнить спектральное разложение периодического сигнала, используя систему базисных функций, состоящую из экспонент с мнимыми показателями:
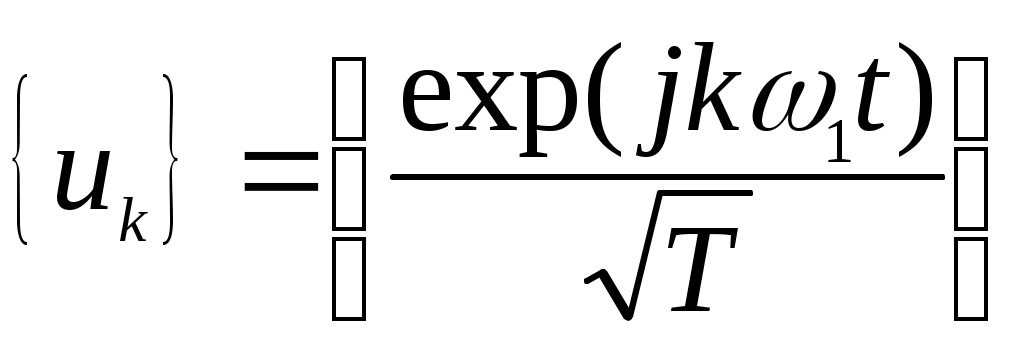 , где
, где 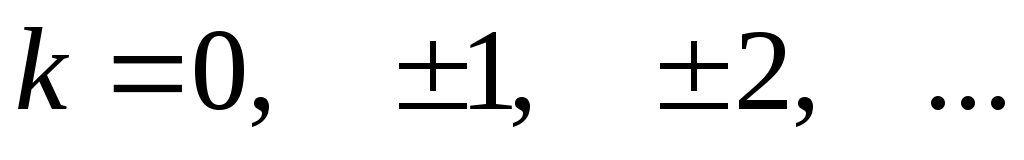 (2.12)
(2.12)
В этом случае форма записи ряда Фурье будет выглядеть следующим образом:
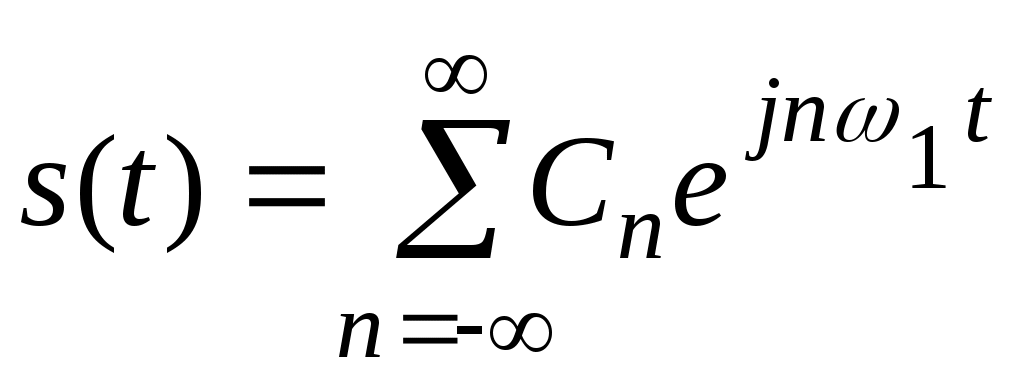 (2.13)
(2.13)
А коэффициенты определяются по формуле:
 (2.14)
(2.14)
Совокупность коэффициентов Cn ряда Фурье в базисе тригонометрических функций называется частотным спектром периодического сигнала.
При разложении периодического сигнала s(t) в ряд Фурье по тригонометрическим функциям в качестве ортогональной системы берут
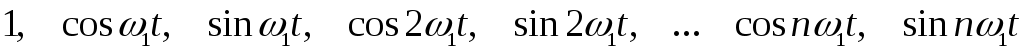 (2.15)
(2.15)
или
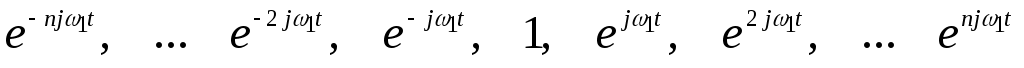 (2.16)
(2.16)
Интервал ортогональности в обоих случаях совпадает с периодом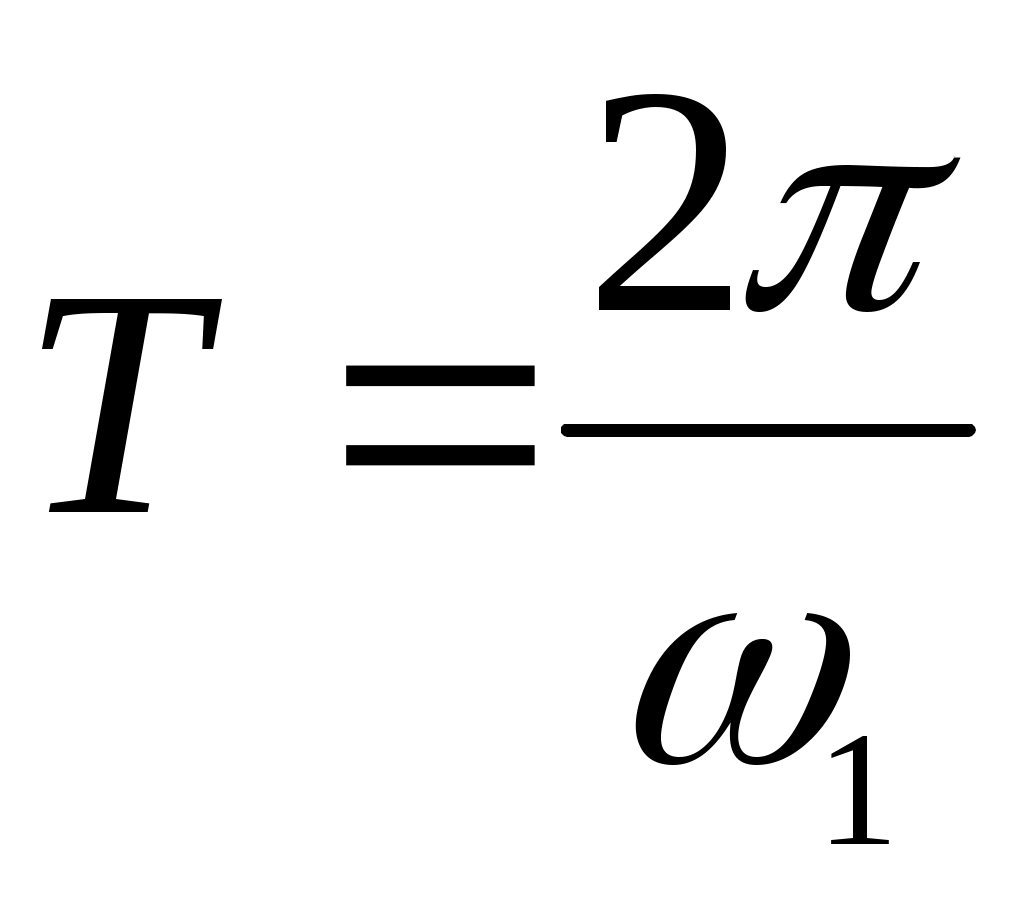 функции s (t).
функции s (t).
Система функций (2.15) приводит к тригонометрической форме ряда Фурье, а система (2.16) — к комплексной форме. Между этими двумя формами существует простая связь.
Выражение (2.13) – является разложением в ряд Фурье по системе функций (2.16). Данное выражение легко преобразуется к виду:

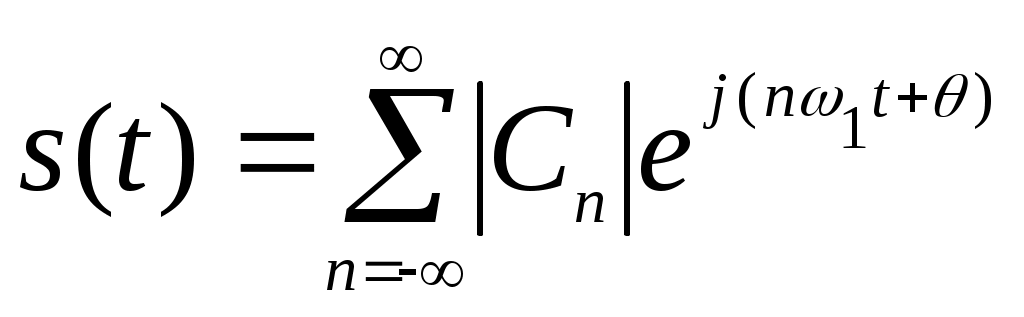 (2.17),
(2.17),
Причем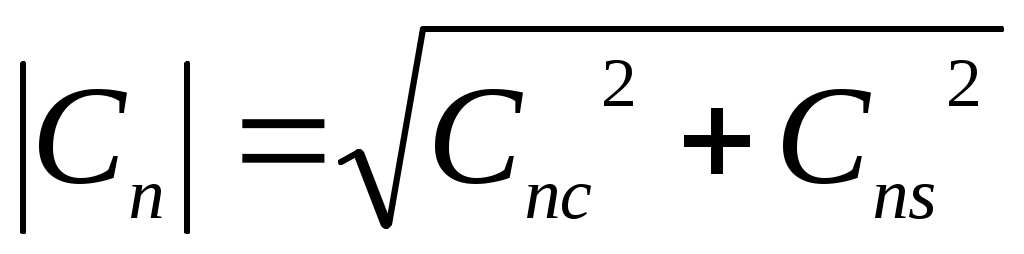 ,
,  , гдеCnc иCns - косинусная (действительная) и синусная (мнимая) части коэффициента Cn, определяемы следующим образом:
, гдеCnc иCns - косинусная (действительная) и синусная (мнимая) части коэффициента Cn, определяемы следующим образом:
 ,
,  (2.18)
(2.18)
Модуль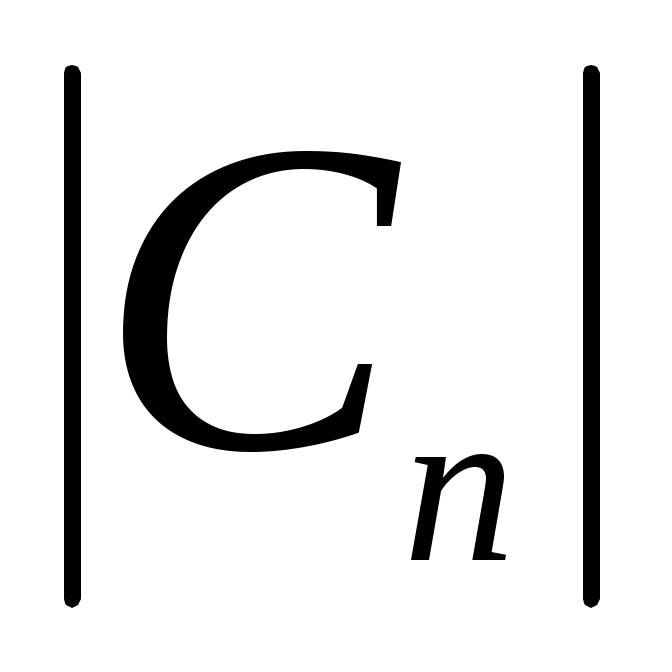 является функцией, четной относительно n, а аргумент θn— нечетной, т.е. Cnc является четной, а Cns – нечетной функциями n.
является функцией, четной относительно n, а аргумент θn— нечетной, т.е. Cnc является четной, а Cns – нечетной функциями n.
Теперь нетрудно перейти к тригонометрической форме ряда Фурье. Выделив из ряда (2.17) пару слагаемых, соответствующую какому-либо заданному значению
Генератор случайных чисел пакета MathCAD генерирует числа с равномерным распределением от 0 до некоторого заданного числа a. Для получения симметричного распределения относительно нуля нужно сместить все выборки случайного сигнала на a/2 вниз.
3. Порядок выполнения работы.
1. Познакомиться с пакетом прикладных программ MathCAD, пользуясь системой помощи.
2. Пользуясь операторами и функциями системы MathCAD разработать алгоритм, моделирующий дискретный аналог меандра для 4-6 периодов. Число единичных (и нулевых) отсчетов взять от 5 до 8.
Построить график дискретного аналога меандра.
3. Используя тригонометрические функции разработать алгоритм, моделирующий дискретный аналог гармонического колебания для 3-4 периодов.
4. Используя программу генерирования случайных чисел смоделировать отсчеты случайного процесса с равномерным распределением в амплитудном диапазоне -1≤n(k)≥1.Число отсчетов взять равным от 50 до 100.
5
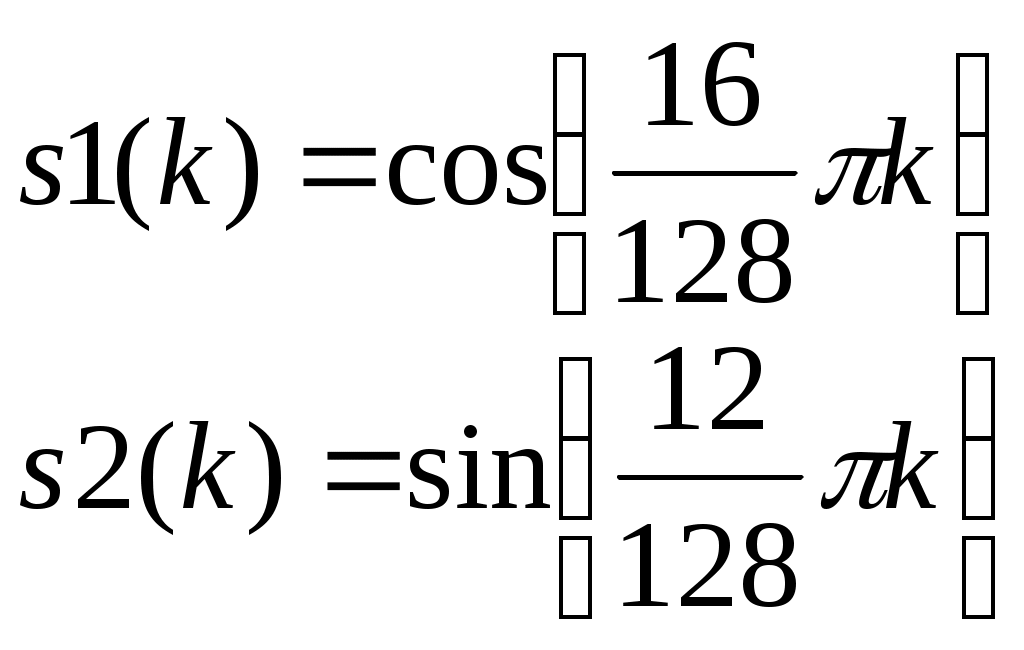
. Смоделировать отсчеты аддитивной смеси двух гармонических сигналов и шума для отношения с/ш = от 1 до 5 по напряжению для 128 отсчетов. Гармонические дискретные сигналы заданы выражениями
где k - номер отсчета
Построить графики сигнала, шума, смеси сигнала с шумом.
6. Распечатать графики дискретных аналогов меандра, дискретной гармонической последовательности для различных фазовых углов дискретизации, дискретной последовательности отсчетов сигнала, шума и смеси сигнал + шум.
7. Индивидуальное задание по построению дискретных аналогов сигналов выдается персонально для каждого студента преподавателем после выполнения общей части лабораторной работы.
4. Содержание отчета.
Отчет должен содержать распечатки программ моделирования испытательных сигналов и графики моделей дискретных сигналов, рассмотренных в пп.3.2 - 3.5.
5. Контрольные вопросы.
1.Какой сигнал называется меандром?
2.Какой сигнал называется детерминированным?
3.Какой сигнал называется случайным?
4.Какой сигнал называется дискретной гармонической последовательностью?
5.Почему удобнее задавать шаг дискретизации через фазовый угол?
6.О чем говорит теорема Котельникова?
7.В какую сторону нужно изменить фазовый угол дискретизации, чтобы увеличить или уменьшить частоту сигнала при неизменном временном шаге дискретизации?
ЛИТЕРАТУРА
1.Гоноровский И.С. Радиотехнические цепи и сигналы.
2.Конспект лекций по курсу "Теоретические основы информационной техники".
ЛАБОРАТОРНАЯ РАБОТА № 2
Вычисление спектра сигналов на ЭВМ с помощью БПФ
-
Цель работы:
Научиться находить спектр сигнала с помощью БПФ и по известному спектру находить исходный сигнал с помощью обратного БПФ
-
Краткие теоретические сведения
В линейном пространстве сигналов можно выделить специальное подмножество, играющее роль координатных осей. Говорят, что совокупность векторов {е1 е2, е3, ...}, принадлежащих множеству М, является линейно независимой, если равенство
Система линейно независимых векторов образует координатный базис в линейном пространстве. Если дано разложение некоторого сигнала s(t) в виде
Длину вектора в математике называют его нормой. Линейное пространство сигналов L является нормированным, если каждому вектору
В радиотехнике чаще всего полагают, что вещественные аналоговые сигналы имеют норму
Данная формула в равной мере относится как к аналоговым, так и к дискретным сигналам (из двух возможных значений корня выбирается положительное).
Функция u(t), для которой выполняется условие
называется нормированной функцией, а система нормированных функций u1(t), u2(t)…, в которой две различные функции взаимно ортогональны, называется ортонормированной системой.
Квадрат нормы носит название энергии сигнала
Определять норму сигнала с помощью формулы (2.1) целесообразно по следующим причинам:
1. В радиотехнике о величине сигнала часто судят, исходя из суммарного энергетического эффекта, например количества теплоты, выделяемой в резисторе.
2. Энергетическая норма оказывается «нечувствительной» к изменениям формы сигнала, может быть, и значительным, но происходящим на коротких отрезках времени.
Среди разнообразных систем ортогональных функций, которые могут использоваться в качестве базисов для представления радиотехнических сигналов, исключительное место занимают гармонические (синусоидальные и косинусоидальные) функции.
Математической моделью процесса, повторяющегося во времени, является периодический сигнал s(t) со следующим свойством:
Здесь Т — период сигнала.
Два сигнала u и v называются ортогональными, если их скалярное произведение, а значит, и взаимная энергия равны нулю:
Выражение (2.4) называют принципом ортогональности двух сигналов.
Пусть Н — гильбертово пространство сигналов с конечным значением энергии. Эти сигналы определены на отрезке времени [t1, t2], конечном или бесконечном. Предположим, что на этом же отрезке задана бесконечная система функций {u0, u1, u2, ….un, …}, ортогональных друг другу и обладающих единичными нормами:
Говорят, что при этом в пространстве сигналов задан ортонормированный базис.
Разложим произвольный сигнал
в ряд, согласно следующему выражению
Представление (2.7) называется обобщенным рядом Фурье сигнала s(t) в выбранном базисе. Коэффициенты Cn определяются по формуле:
 (2.8)
(2.8)Совокупность полученных коэффициентов Cn называют спектром сигнала s(t ) в ортогональной системе u(t) и полностью определяют этот сигнал.
Введем основную частоту
с коэффициентами :

 (2.10)
(2.10)
Итак, в общем случае периодический сигнал содержит не зависящую от времени постоянную составляющую и бесконечный набор гармонических колебаний, так называемых гармоник с частотами
Каждую гармонику можно описать ее амплитудой Аn начальной фазой φn . Для этого коэффициенты ряда Фурье следует записать в виде:
Так что (2.11)
Подставив эти выражения в (2.9), получим другую, эквивалентную форму ряда Фурье:
Спектральной диаграммой периодического сигнала принято называть графическое изображение коэффициентов ряда Фурье для конкретного сигнала. Различают амплитудные и фазовые спектральные диаграммы.
Для того, чтобы получить комплексную форму ряда Фурье, необходимо выполнить спектральное разложение периодического сигнала, используя систему базисных функций, состоящую из экспонент с мнимыми показателями:
В этом случае форма записи ряда Фурье будет выглядеть следующим образом:
А коэффициенты определяются по формуле:
 (2.14)
(2.14)Совокупность коэффициентов Cn ряда Фурье в базисе тригонометрических функций называется частотным спектром периодического сигнала.
При разложении периодического сигнала s(t) в ряд Фурье по тригонометрическим функциям в качестве ортогональной системы берут
или
Интервал ортогональности в обоих случаях совпадает с периодом
Система функций (2.15) приводит к тригонометрической форме ряда Фурье, а система (2.16) — к комплексной форме. Между этими двумя формами существует простая связь.
Выражение (2.13) – является разложением в ряд Фурье по системе функций (2.16). Данное выражение легко преобразуется к виду:
Причем
 ,
,  (2.18)
(2.18)Модуль
Теперь нетрудно перейти к тригонометрической форме ряда Фурье. Выделив из ряда (2.17) пару слагаемых, соответствующую какому-либо заданному значению

