МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Уфимский государственный нефтяной технический университет» (ФГБОУ ВО УГНТУ)

Институт нефтепереработки и нефтехимии ФГБОУ ВО УГНТУ в г. Салавате

Кафедра «Информационных технологий»

Физика
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА
Молекулярная физика. Термодинамика.
ИнТех- 09.03.01 – 1.02.09 РГР

Исполнитель:

студент гр. БАБз - 22-21 Юрлов Р. В.

Руководитель:

ассистент Г.Ф. Шаяхметов

Салават

2023

2.9. Определить относительную молекулярную массу :

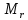1) воды,

2) углекислого газа,

3) поваренной соли.

Дано:

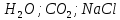
Найти:

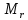
Решение.

1) Одна молекула 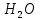состоит из одного атома кислорода и двух атомов водорода. Молярная масса кислорода 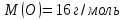, а водорода 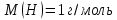. Тогда молярная масса молекулы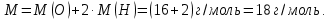



Поэтому относительная молекулярная масса равна .

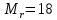2) Одна молекула 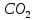состоит из одного атома углерода и двух атомов кислорода. Молярная масса углерода 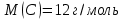, а кислорода 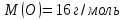. Тогда молярная масса молекулы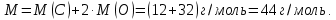



Поэтому относительная молекулярная масса равна

---

.

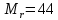
3) Одна молекула 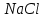состоит из одного атома натрия и одного атома хлора. Молярная масса натрия 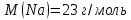, а хлора 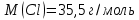. Тогда молярная масса молекулы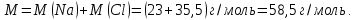



Поэтому относительная молекулярная масса равна .

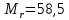Ответ:

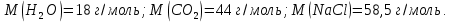
2.19. Определить плотность 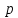водяного пара, находящегося под давлением 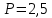кПа и имеющего температуру 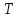= 250К.

Дано:_СИ'>Дано:

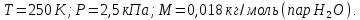
СИ:

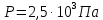
Найти:

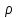
Решение.

Воспользуемся уравнением Клапейрона – Менделеева, применив его к пару:



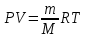
где 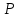– давление пара, Па;

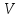- объем, ;

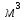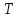– температура газа, К;

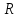– молярная газовая постоянная (8,31Дж/(моль·К)).

Откуда

.

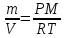Нам известно, что плотность

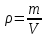
Поэтому



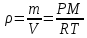
Проверим размерности расчетных формул



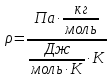
Подставляя числовые значения получим ответ



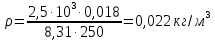
Ответ:

---

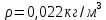
2.29. В азоте взвешены мельчайшие пылинки, которые движется так, как если бы они были очень крупными молекулами. Масса каждой пылинки равна 6 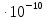г. Газ находится при температуре = 400 К. Определить средние квадратичные скорости 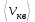, а также средние кинетические энергии 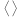поступательного движения молекулы азота.

Дано:

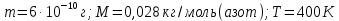
СИ:

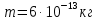
Найти: ; .

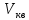Решение.

По определению среднеквадратичная скорость



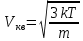
где 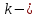постоянная Больцмана (1,38 ;

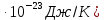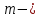масса пылинки, кг.

Поэтому скорость пылинки



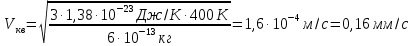
С другой стороны среднеквадратичная скорость

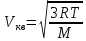
где ;

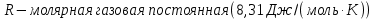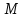-молярная масса газа.

Поэтому скорость молекул азота



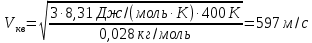
Средняя кинетическая энергия поступательного движения одной молекулы



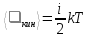
Где 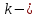постоянная Больцмана (1,38 ;

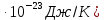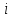
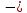поступательные степени свободы молекулы (в нашем случае 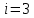, т.к. возможны три поступательных движения).

Поэтому

---

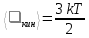
Средняя энергия поступательно движения пылинки равна



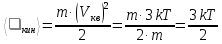
Видно, что средние кинетические энергии пылинки и молекул азота равны друг другу

Проверим размерности расчетных формул



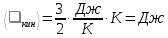
Подставляя числовые значения получим ответ

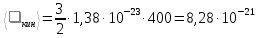Дж

Ответ:_Дж1.39.'>Ответ: 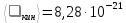Дж

1.39. Одноатомный газ при нормальных условиях занимает объем 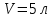. Вычислить теплоемкость 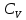этого газа при постоянном объеме.

Дано:

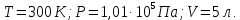
СИ:

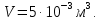
Найти: .

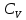Решение.

Изохорная теплоемкость равна



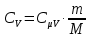
где

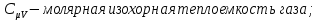
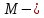молекулярная масса газа, кг.

Воспользуемся уравнением Клапейрона – Менделеева:



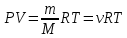
где 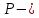давление, Па;

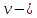количество молей;

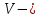объем сосуда,

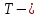температура газа, К;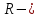

.

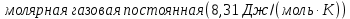Откуда



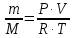
Поэтому



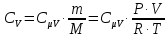
С другой стороны, молярная теплоемкость при постоянном объеме равна



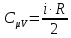
где

---

число степеней свободы (в нашем случае число степеней свободы равно 3 (3 поступательные и ни одной вращательной, т.к. газ одноатомный));

.

тогда



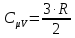
Подставим



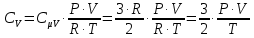
Проверим размерности расчетных формул



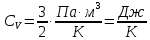
Подставляя числовые значения получим ответ

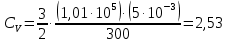Дж/К

Ответ: 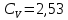Дж/К

2.49. Определить количество теплоты 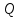, которое надо сообщить кислороду объемом 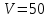л при его изохорном нагревании, чтобы давление газа повысилось н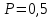а МПа.

Дано: 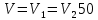л;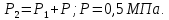

СИ:

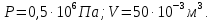
Найти:

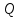
Решение.

Количество тепла 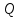, необходимое для изохорного нагрева газа определяется: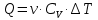



Где количество молей газа;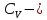

молярная изохорная теплоемкость;

Молярная изохорная теплоемкость вычисляется:



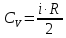
где число степеней свободы газа (в нашем случае i=5, т.к. кислород – газ двухатомный (3 поступательные и 2 вращательные степени свободы)

поэтому



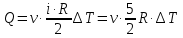
Воспользуемся уравнением Клапейрона – Менделеева, применив его к газу:

---

Смотрите также файлы

• Решение задачи 1 Решение задачи 2.docx

• Білімділік.docx

• Это идентификатор товарной позиции, единица учета запасов, складской номер, используемый в торговле для отслеживания статистики по реализованным товарам или услугам.docx

• Лабораторная работа 15. Тестирование интеграции Цель занятия Изучение назначения и задач интеграционного тестирования.docx

• В широком смысле.docx