Файл: Лабораторная работа 8 Исследование простейшей демографической модели Мальтуса.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.04.2024
Просмотров: 25
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Представим дифференциальное уравнение в виде
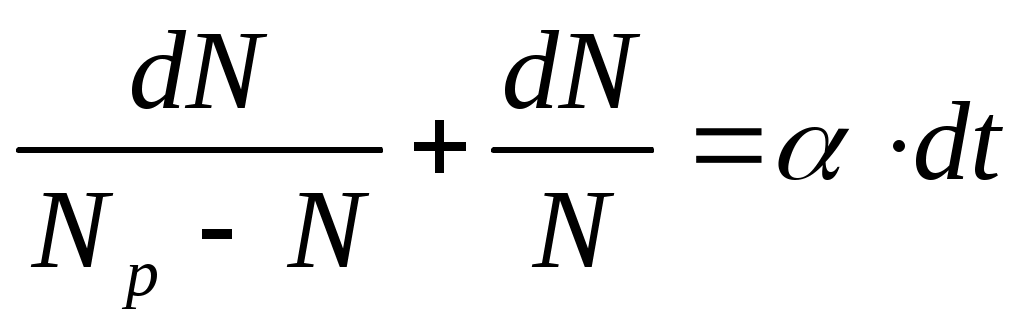, проинтегрировав его, получим
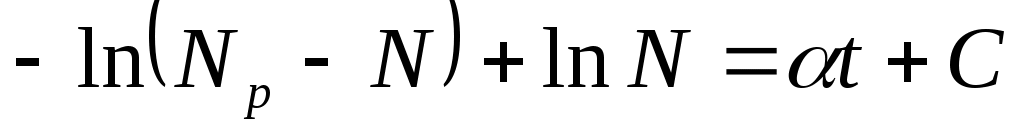
Постоянную интегрирования определим из условия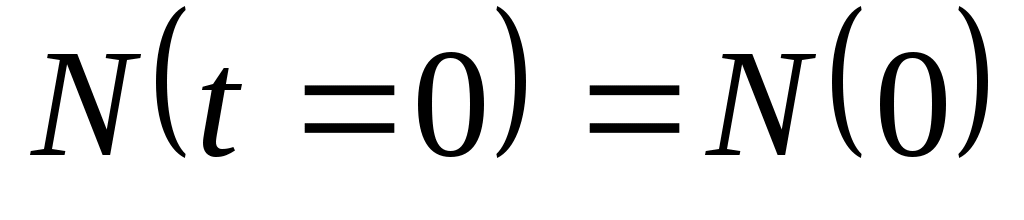
, т.е. 
.
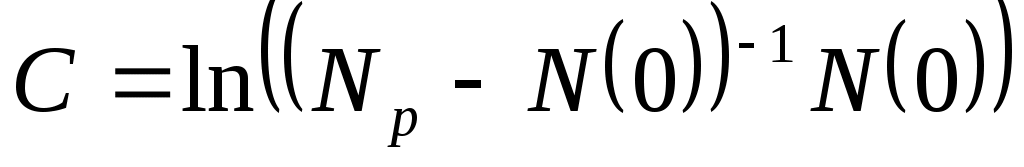В результате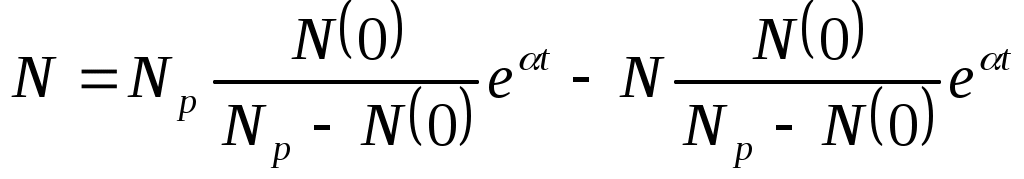
Или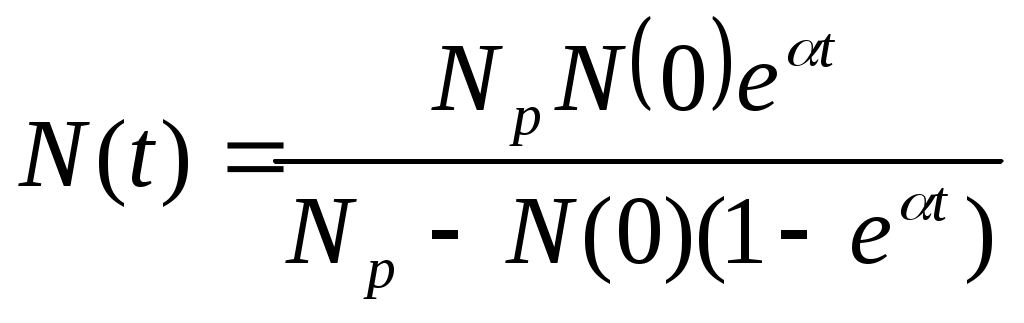
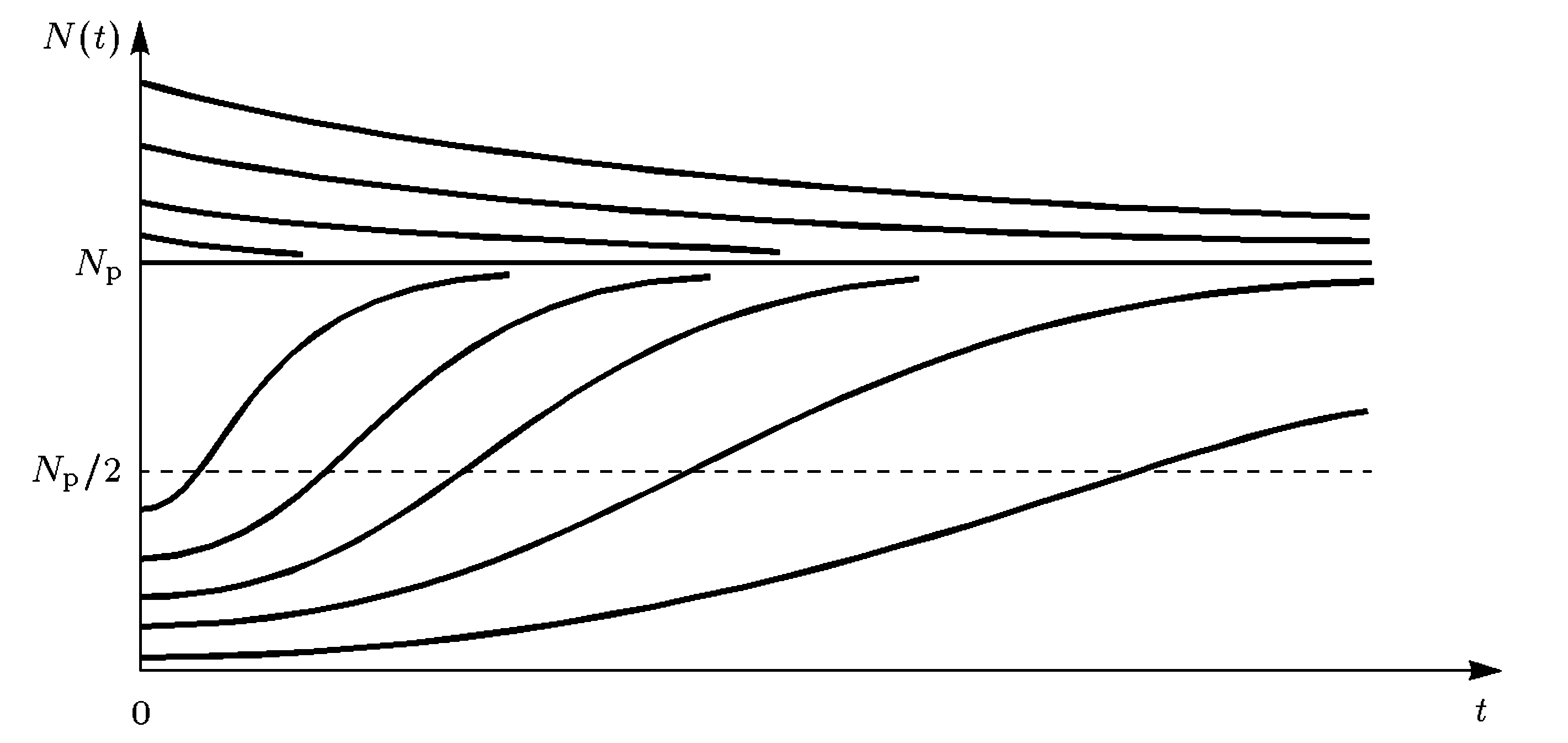
3 Логистические кривые, соответствующие различным значениям начальной численности N(0)
Поведение функции N(t) описывается логистической кривой. При любом N(0) численность стремится к равновесному значению Np, причем тем медленнее, чем величина N(t) ближе к N(0). Т.о. в данной модели равновесие устойчиво (в отличие от модели, рассмотренной в первом примере).
Создадим функцию yp.m
function dN=yp(t,N)
alfa=0.1;
Np=2000;
dN=N*(Np-N)*alfa/Np;
С помощью процедуры ode45 для численного решения задачи Коши найдем решение уравнения Ферхюльста.
Зададим значения начальной и равновесной численности популяции, общее время роста и построим график, иллюстрирующий зависимость численности популяции от времени:
N0=input('Введите первоначальную численность населения N0, меньшую 2000 ');
Np=2000;
plot(t,Np,'b')
grid on
hold on
for N00=N0:200:Np+N0
[t,N]=ode45('yp',0:0.01:50,[N00]);
if N00
plot(t,N,'r')
elseif N00==Np
plot (t,N)
elseif N00>Np
plot(t,N, 'g')
end
end
title('изменение численности популяции')
xlabel('t')
ylabel('N(t)')
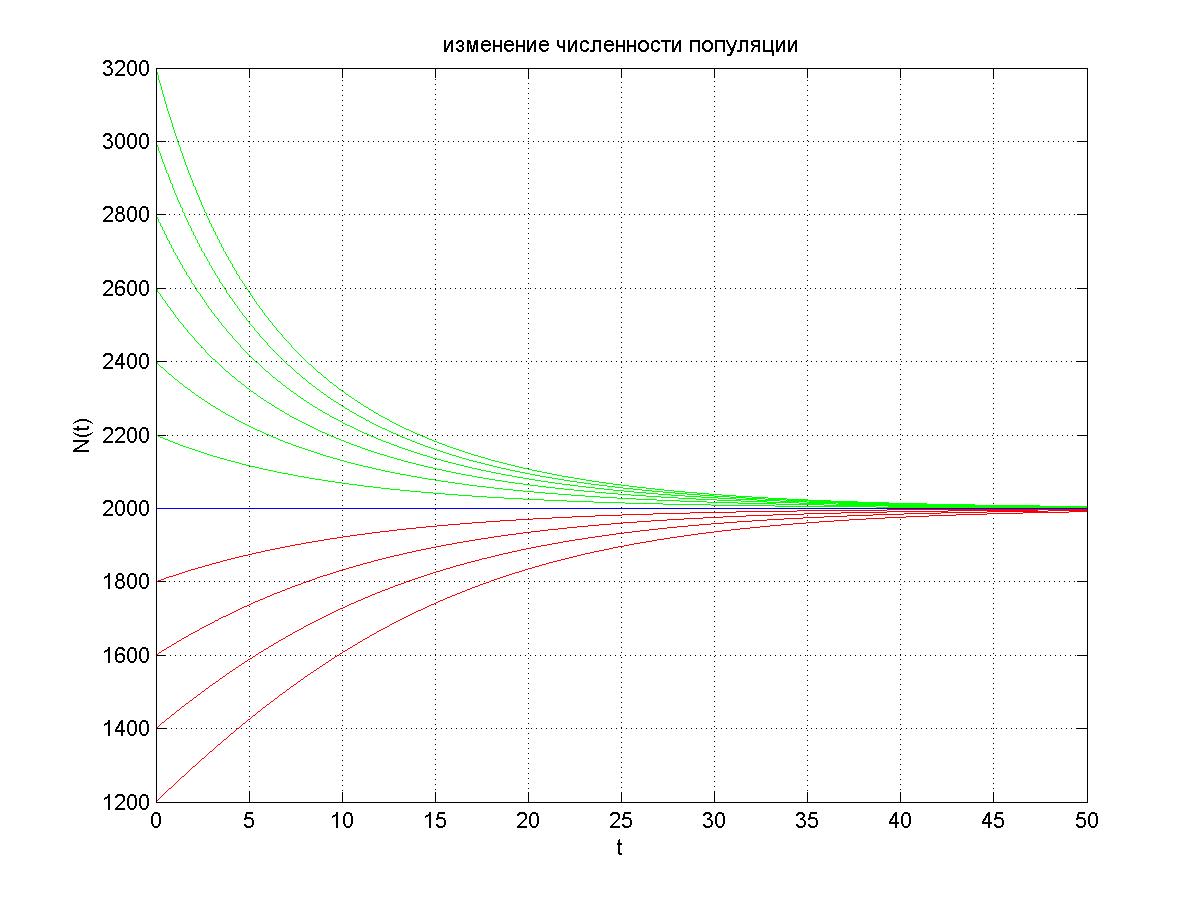
4 График изменения численности популции по модели Мальтуса – Ферхюльста
Логистическая модель более реалистично отражает динамику популяции по сравнению с моделью Мальтуса.
Представим дифференциальное уравнение в виде
, проинтегрировав его, получим Постоянную интегрирования определим из условия
, т.е. .В результате
Или
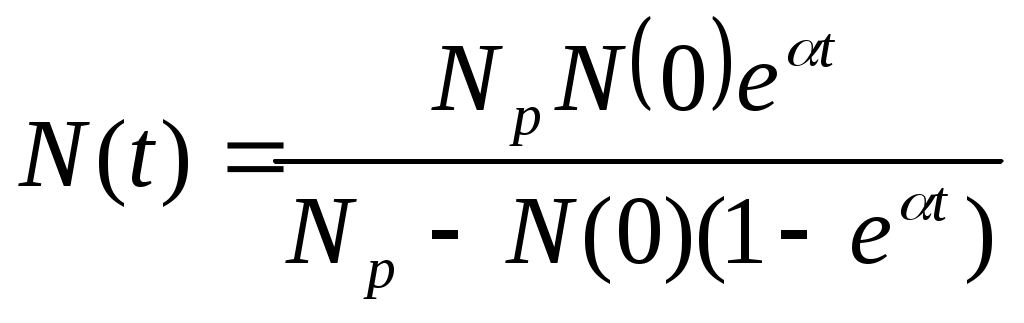
3 Логистические кривые, соответствующие различным значениям начальной численности N(0)
Поведение функции N(t) описывается логистической кривой. При любом N(0) численность стремится к равновесному значению Np, причем тем медленнее, чем величина N(t) ближе к N(0). Т.о. в данной модели равновесие устойчиво (в отличие от модели, рассмотренной в первом примере).
-
Реализация задач в MATLAB
Создадим функцию yp.m
function dN=yp(t,N)
alfa=0.1;
Np=2000;
dN=N*(Np-N)*alfa/Np;
С помощью процедуры ode45 для численного решения задачи Коши найдем решение уравнения Ферхюльста.
Зададим значения начальной и равновесной численности популяции, общее время роста и построим график, иллюстрирующий зависимость численности популяции от времени:
N0=input('Введите первоначальную численность населения N0, меньшую 2000 ');
Np=2000;
plot(t,Np,'b')
grid on
hold on
for N00=N0:200:Np+N0
[t,N]=ode45('yp',0:0.01:50,[N00]);
if N00
plot(t,N,'r')
elseif N00==Np
plot (t,N)
elseif N00>Np
plot(t,N, 'g')
end
end
title('изменение численности популяции')
xlabel('t')
ylabel('N(t)')
4 График изменения численности популции по модели Мальтуса – Ферхюльста
-
Выводы
Логистическая модель более реалистично отражает динамику популяции по сравнению с моделью Мальтуса.