Министерство образования и науки ЛНР
Государственное образовательное учреждение
среднего профессионального образования
Луганской Народной Республики
«Краснодонский промышленно-экономический колледж»
 Счетные множества и их свойства. Счетность множества рациональных и алгебраических чисел. Несчетность множества действительных чисел. Существование трансцендентных чисел.

Устное сообщение по дисциплине
«Дискретная математика»
студента группы 1КСК-20
Редькина Ильи Константиновича

Краснодон, 2022

Свойства счетных множеств:

1) Множество называется счетным, если оно равномощно множеству N. (2 множества называются равномощными, если одно из них можно биективно отобразить на другое).

2) Множество называется счетным, если все его элементы можно занумеровать, используя по одному разу все натуральные числа.

3) Бесконечное множество, отличное от счетного, называется несчетным.

4) Всякое бесконечное подмножество счетного множества счетно.

5) Если к бесконечному множеству добавить счетное или конечное множество, то его мощность не изменится.

6) объединение конечного числа счетных множеств счетно.

7) Объединение счетного семейства счетных множеств счетно.

8) Объединение счетного семейства конечных множеств счетно или конечно.

9) Объединение счетного и конечного множеств счетно.

10) Не существует бесконечных множеств мощностью меньше чем счетное.

11) Если из бесконечного несчетного множества удалить счетное или конечное, то его мощность не изменится.

12) Если некоторое множество представить в виде прямого произведения конечного числа счетных, то оно само является счетным.

Док: рассмотрим числа вида p/q (p – целое, q - натуральное). Q1 – множество чисел, стоящих в числителе, это целые числа, Q1 счетное множество. Q2 – множество чисел в знаменателе, это натуральные числа, Q2 – счетное множество. Имеем объединение счетного семейства счетных чисел. Т. о. множество Q рациональных чисел счетно.

Счетность множества рациональных и алгебраических чисел

ОПРЕДЕЛЕНИЕ

Число x называется алгебраическим, когда оно является корнем какого-либо многочлена с целыми коэффициентами, в противоположном случае оно называется трансцендентным.

---

ТЕОРЕМА

Множество всех алгебраических чисел является счетным

ДОКАЗАТЕЛЬСТВО

Сперва всего заметим, что множество всех многочленов с целыми коэффициентами будет счетным. Это получается из итога: Множество всех многочленов Рn(x)=a0xn+a1xn–1+...+an с рациональными коэффициентами, является счетным.

теоремы: Множество Q всех рациональных чисел является счетным, и теоремы: Любое бесконечное подмножество счетного множество является счетным.

Поскольку каждый многочлен имеет конечное множество корней, потому множество всех алгебраических чисел является объединением счетного множества конечных множеств. Когда применить теорему: Объединение счетного множество конечных множеств, которые попарно не пересекаются, ест счетное множество, и учесть тот факт, что все алгебраические числа образовывают бесконечное множество, то согласно теореме: Любое бесконечное подмножество счетного множество является счетным.

мы получаем, что оно будет счетным.

Несчетность множества действительных чисел

ТЕОРЕМА

Множество действительных чисел несчётно.

ДОКАЗАТЕЛЬСТВО

Предположим противное, пусть множество действительных чисел счетное. Тогда любое подмножество счетного множества тоже счетное. Возьмём на множестве действительных чисел подмножество R1 - интервал (0,1) и выкинем из этого отрезка числа, содержащие хотя бы в одном своём разряде нули или девятки (примеры таких чисел: 0.9, 0.0001 и т. д.). Множество R2, составленное из оставшихся чисел, является подмножеством множества R1 . Это означает, что R2 – счетное.

Из того факта, что R2 – счетное, напрямую следует, что возможен какой-либо способ перечисления его элементов для установления взаимно-однозначного соответствия между элементами R2 и элементами множества натуральных чисел. Это следует из самого определения мощности множества, согласно которому предполагается, что в равномощных множествах каждый элемент одного множества имеет парный элемент из другого множества и наоборот. Обратите внимание, фундаментальное отличие данного определения от определения эффективной перечислимости состоит в том, что в данном случае мы даже не говорим о наличии какого-либо алгоритма перечисления, мы просто утверждаем, что можно привести список действительных чисел из множества R2 и список соответствующих им натуральных чисел из множества N. Алгоритм построения связи N ↔ R2 нас в

---

данном случае не интересует, достаточно того, что такое соответствие возможно.

Существование трансцендентных чисел

Существуют ли трансцендентные числа? В настоящей заключительной главе мы дадим ответ на этот вопрос. Легко указать трансцендентное число. Совсем иное дело доказать его трансцендентность. То число а, трансцендентность которого мы установим, имеет следующую важную особенность: его десятичное разложение в основном состоит из нулей. Оно равно



где единицы стоят на местах с номерами



т. е. на местах с номерами



Символ  , где k — натуральное число, читается k факториал и обозначает произведение всех натуральных чисел от 1. до 



Все цифры в десятичном разложении числа а, за исключением тех, номера которых выражаются факториалами целых чисел, равны нулю. Следовательно, а можно записать в виде следующей суммы отрицательных степеней 10:



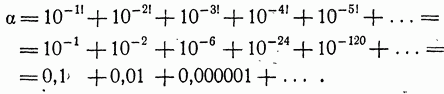
Указанное число а называется числом Лиувилля, по имени французского математика, впервые доказавшего существование трансцендентных чисел.

---

Смотрите также файлы

• Научное исследование. Этапы научно исследовательской работы.docx

• ысамерзімді жоспар 5саба Сабаты таырыбы Бірлесіп орындалатын жмыстара атысты в нса есептерін шыару.doc

• .docx

• Приемапередачи.doc

• Ввод информации в память компьютера.ppt