ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.04.2024
Просмотров: 5
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования
«Тольяттинский государственный университет»
| (наименование института полностью) |
| |
| (Наименование учебного структурного подразделения) |
| |
| (код и наименование направления подготовки / специальности) |
| |
| (направленность (профиль) / специализация) |
Практическое задание №1
по учебному курсу « Физика 1 »
(наименование учебного курса)
Вариант __14_ (при наличии)
| Обучающегося | А.А. Попова | |
| | (И.О. Фамилия) | |
| Группа | ЭЭТбп-2001в | |
| | | |
| Преподаватель | Н.М. Смоленская | |
| | (И.О. Фамилия) | |
Тольятти 2022
Практическая работа 1
Задача 1
Частица движется равноускоренно в координатной плоскости ху с начальной скоростью
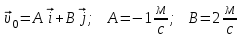 и ускорением
и ускорением 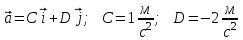 . Найти модули векторов скорости
. Найти модули векторов скорости 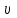 , тангенциального
, тангенциального 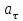
и нормального
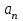 ускорений, а также радиус кривизны R траектории в момент времени
ускорений, а также радиус кривизны R траектории в момент времени 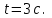
| Дано: 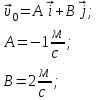 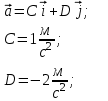 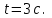 | Решение: Запишем координаты вектора начальной скорости: 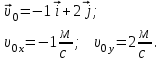 Запишем координаты вектора ускорения: 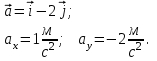 Следовательно, в направлении оси х движении равноускоренно и в направлении оси у равноускоренно. Запишем уравнение траектории частицы в параметрическом виде. 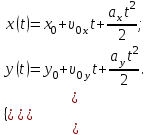 За начало координат принимаем точку с координатами 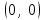 . После подстановки соответственных значений, получаем: . После подстановки соответственных значений, получаем: |
| Найти: 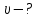 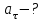 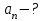 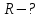 | |
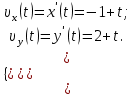 Для момента времени 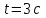 , получаем: , получаем: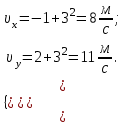 Тогда модуль вектора скорости будет: 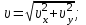 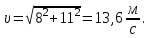 Для определения тангенциального  и нормального и нормального 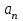 ускорений, а также радиус кривизны Rпостроим график траектории точки (Рис. 2). ускорений, а также радиус кривизны Rпостроим график траектории точки (Рис. 2). Вычисляем полное ускорение по формуле: 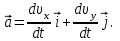 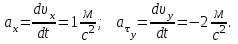 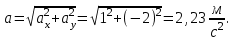 Тангенс угла, который образует касательная к траектории в момент времени 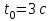 , вычисляется по формуле: , вычисляется по формуле: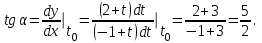 Тогда 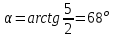 . .Согласно рисунку 2: 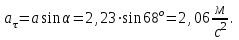 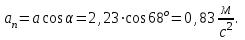 Нормальное ускорение вычисляется по формуле: 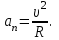 Откуда 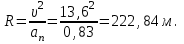 Ответ: 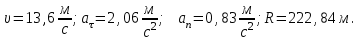 | |
Задача 2
На однородный цилиндрический блок массой
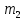 и радиусом R намотана невесомая нить, к свободному концу которой прикреплен груз массой
и радиусом R намотана невесомая нить, к свободному концу которой прикреплен груз массой 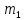 . К блоку крестообразно прикреплены четыре одинаковых невесомых стержня, на которых закреплены одинаковые грузы массой
. К блоку крестообразно прикреплены четыре одинаковых невесомых стержня, на которых закреплены одинаковые грузы массой 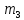 на расстоянии x от оси вращения. Грузы
на расстоянии x от оси вращения. Грузы 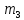 можно считать материальными точками. Трением в блоке можно пренебречь. Найти зависимость ускорения a груза
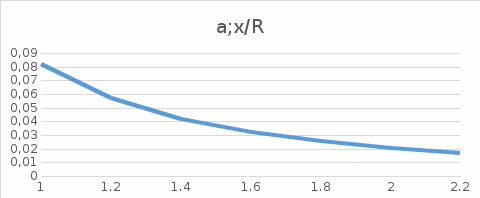
можно считать материальными точками. Трением в блоке можно пренебречь. Найти зависимость ускорения a груза 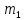 от расстояния x. Построить график этой зависимости в интервале изменения x от R до 3R. Ускорение свободного падения g=9.81 м/
от расстояния x. Построить график этой зависимости в интервале изменения x от R до 3R. Ускорение свободного падения g=9.81 м/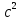 .
. R=0.1м
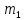 =10кг
=10кг 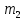 =2кг
=2кг 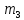 =3кг
=3кг
Решение:
M=
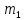 gR – Вращающий момент силы
gR – Вращающий момент силы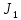 =
=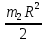 – Момент инерции блока
– Момент инерции блока =4
=4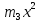 – момент инерции четырёх грузов
– момент инерции четырёх грузовУравнение движения для блока (
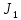 +
+ )Ɛ=M => (
)Ɛ=M => (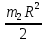 + 4
+ 4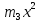 )Ɛ=
)Ɛ=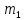 gR
gRƐ=
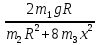 - Угловое ускорение блока
- Угловое ускорение блока Линейное ускорение груза a= ƐR=
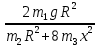 => a=
=> a=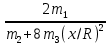
g
a=
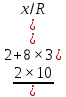 ×9,81=
×9,81=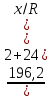
Задача 3
Шар массой
 , летящий со скоростью
, летящий со скоростью 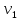 , сталкивается с неподвижным шаром массой
, сталкивается с неподвижным шаром массой  . После удара шары разлетаются под углом α друг к другу. Удар абсолютно упругий, столкновение происходит в горизонтальной плоскости. Найти скорости шаров
. После удара шары разлетаются под углом α друг к другу. Удар абсолютно упругий, столкновение происходит в горизонтальной плоскости. Найти скорости шаров 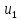 и
и 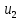 после удара.
после удара. = 130г
= 130г  = 110г
= 110г 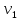 = 10 м/с α= 30
= 10 м/с α= 30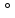
Решение:
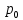 =
= 
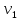
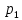 =
= 
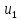
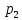 =
= 
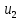
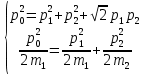
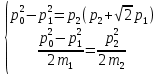
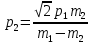
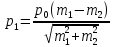
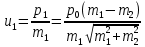 =
=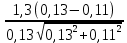 =
=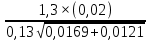 =
=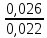 =1,18 (м/с)
=1,18 (м/с)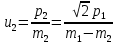 =
=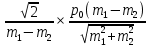
=
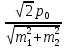 =
=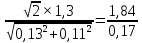 =10,82 (м/с)
=10,82 (м/с)

