Файл: Общая электротехника и электроника учебнометодический комплекс.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.05.2024
Просмотров: 118
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
u и i, а также векторные диаграммы.
3. Основные расчетные соотношения.
4. Таблица по форме 2.1 с результатами измерений и вычислений.
5. Краткие выводы.
5. ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Чем отличаются идеализированные элементы электрической цепи от реальных элементов?
2. Почему в данной работе в качестве идеализированных элементов можно использовать резистор, катушку индуктивности и конденсатор?
3. Для некоторой цепи известны напряжение и ток:
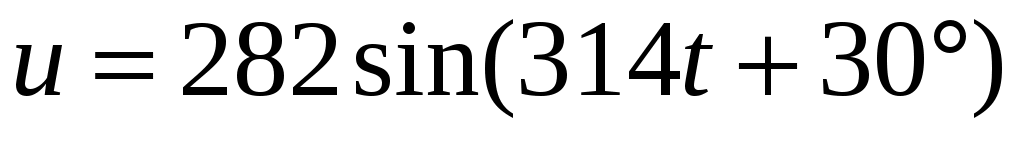 ;
; 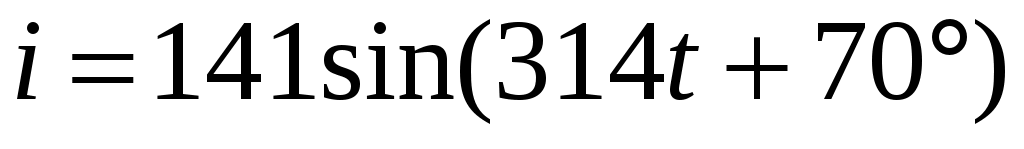 .
.
Требуется определить:
действующие значения напряжения и тока цепи;
частоту цепи f, Гц;
угол сдвига фаз между напряжением и током цепи;
характер цепи индуктивной или емкостной.
Построить графики зависимости тока и напряжения цепи от времени.
Построить векторную диаграмму цепи.
4. В цепи с активным сопротивлением измерены действующие значения тока и напряжения I = 1A; U = 10 B. Требуется определить величину активного сопротивления.
Записать ток и напряжение в виде синусоид, если частота цепи
f = 1000 Гц, а начальная фаза напряжения u = 60. Построить графики зависимости тока и напряжения от времени. Построить векторную диаграмму цепи.
5. В цепи с индуктивностью измерены действующие значения тока и напряжения U =10 B, I = 1A. Требуется:
определить величину индуктивного сопротивления xL;
определить величину индуктивности L, если частота цепи f =1590 Гц;
записать ток и напряжение в виде синусоид, если частота цепи
f = 1590 Гц, а начальная фаза напряжения u = 360;
построить векторную диаграмму цепи.
6. В цепи с емкостью измерены действующие значения тока и напряжения цепи: U = 10 B; I = 1 A. Требуется:
определить величину индуктивного сопротивления xС;
определить величину индуктивности С, если частота цепи f = 1590 Гц;
записать ток и напряжение в виде синусоид, если частота цепи
f =1590 Гц, а начальная фаза напряжения u = 60;
построить векторную диаграмму цепи.
7. Как зависят активное сопротивление R, индуктивное сопротивление xL, и емкостное сопротивление xС от частоты приложенного напряжения?
8. Индуктивное сопротивление цепи составляет 8 Ом. Как изменится это сопротивление, если частоту приложенного напряжения увеличить в два раза?
Л и т е р а т у р а: [2], c. 19...29.
Работа 3. ИССЛЕДОВАНИЕ РАЗВЕТВЛЕННОЙ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА С ОДНИМ ИСТОЧНИКОМ ЭНЕРГИИ
1. ЦЕЛЬ РАБОТЫ
Экспериментальное исследование разветвленной электрической цепи с одним источником синусоидального напряжения и ее расчет комплексным методом.
2. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
В данной работе исследуется цепь, со смешанным соединением трех комплексных сопротивлений Z1, Z2 и Z3. Рассматривается одна из двух схем такой цепи: с последовательно-параллельным (рис. 3.1, а) и параллельно-последовательным (рис. 3.1, б) соединениями этих элементов.
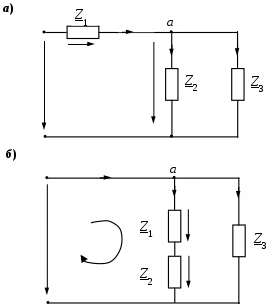
Рис. 3.1
Расчет исследуемой цепи
Задача расчета состоит в определении токов во всех ветвях цепи при известных параметрах, заданном действующем значении приложенного к цепи напряжения и частоте сети. Расчет производится символическим методом (методом комплексных амплитуд) с использованием преобразований цепи либо к последовательному, либо к параллельному соединению ее элементов.
Порядок расчета цепи с последовательно-параллельным
соединением комплексных сопротивлений (рис. 3.1, а)
1. Определяется эквивалентное комплексное сопротивление цепи Zэ
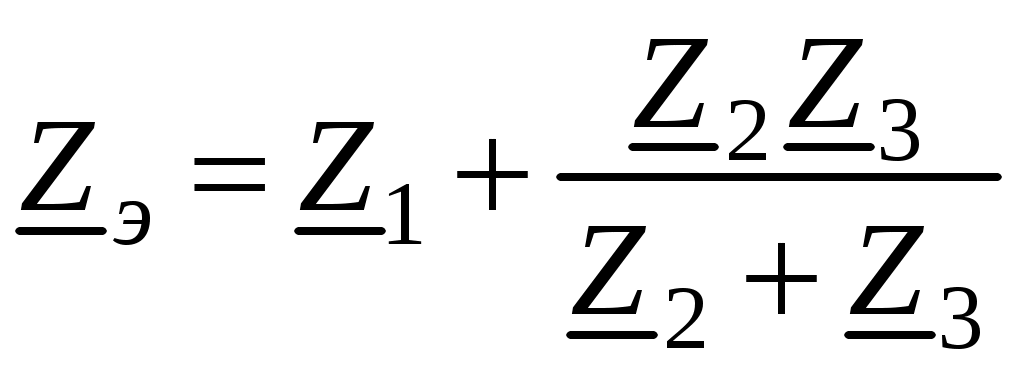 .
.
2. Определяется комплексное действующее значение тока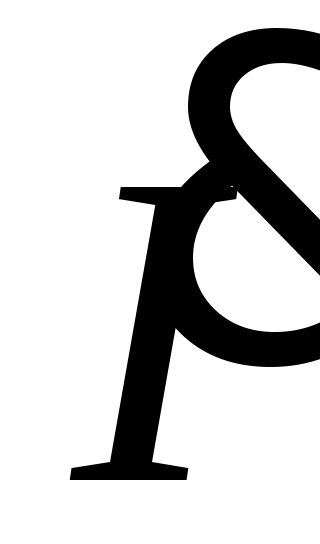
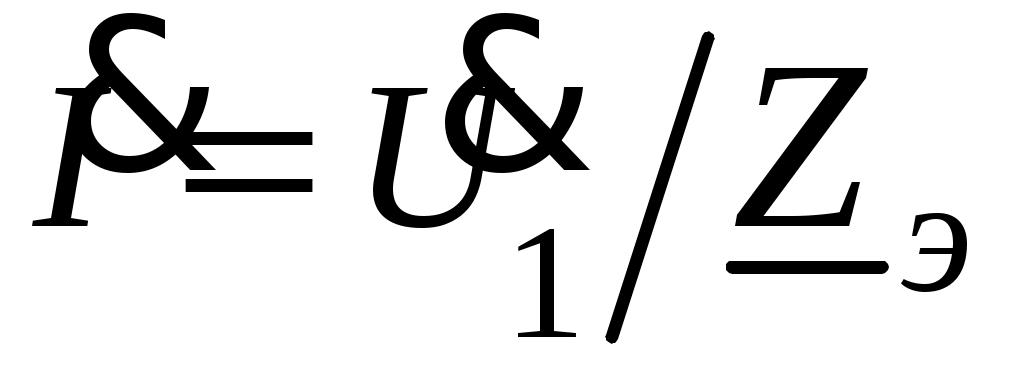 .
.
При этом начальная фаза приложенного напряжения может быть принята равной нулю, т. е.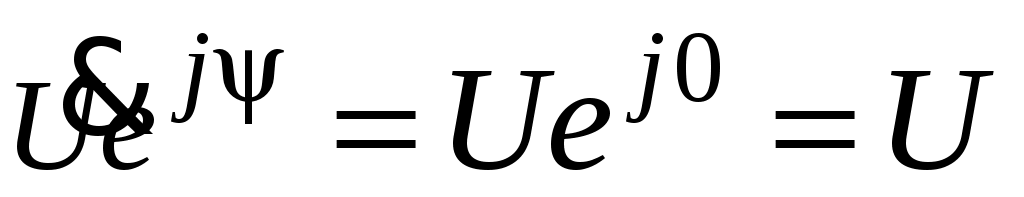 .
.
3. Определяется комплексное действующее значение напряжения на участке цепи с параллельным соединением Z2 и Z3
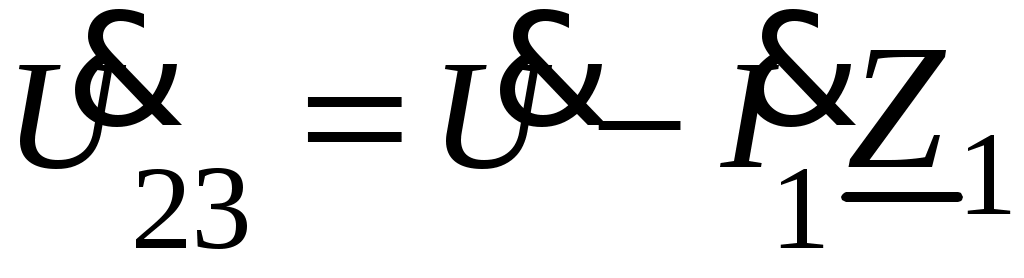 .
.
4. Определяется комплексное действующее значение тока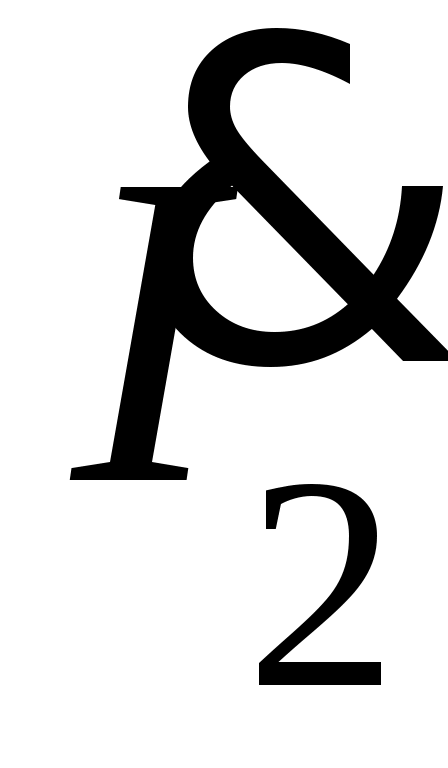
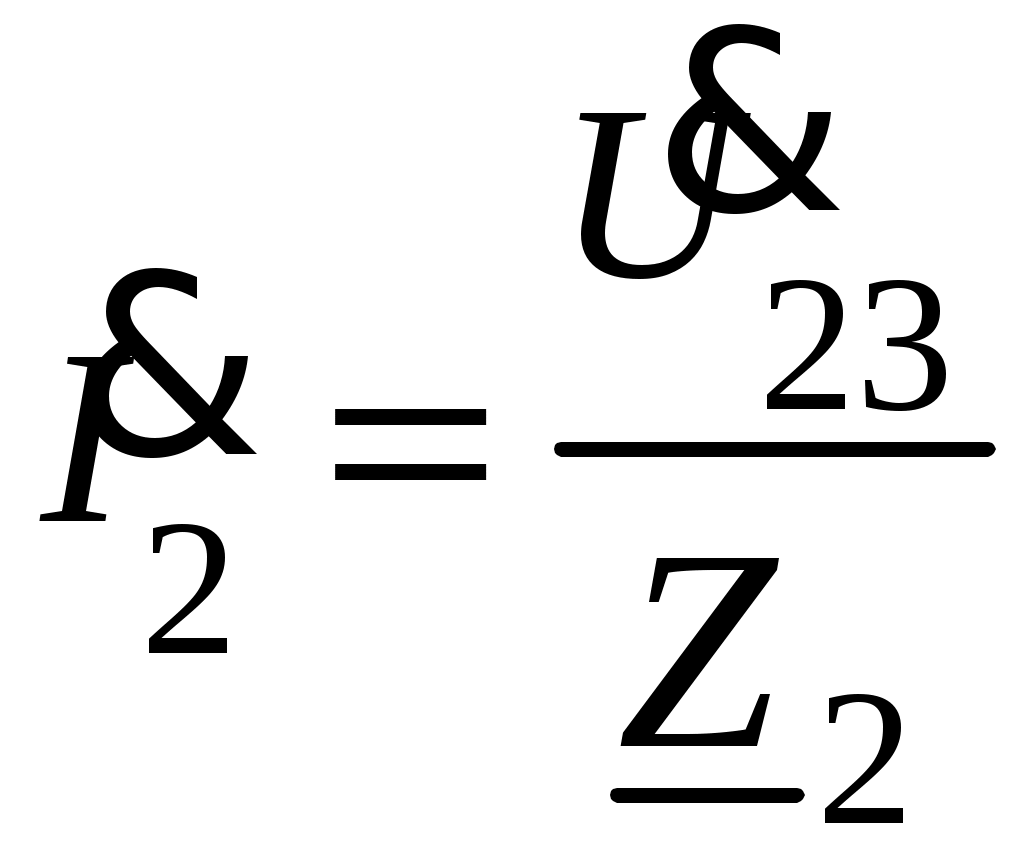 .
.
5. Определяется комплексное действующее значение тока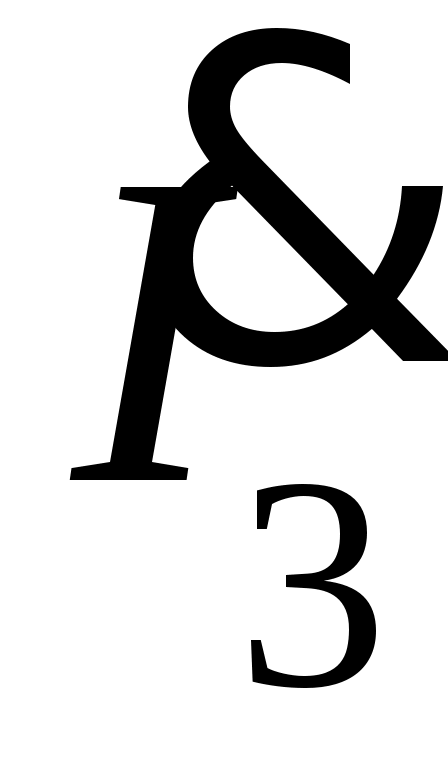 :
:
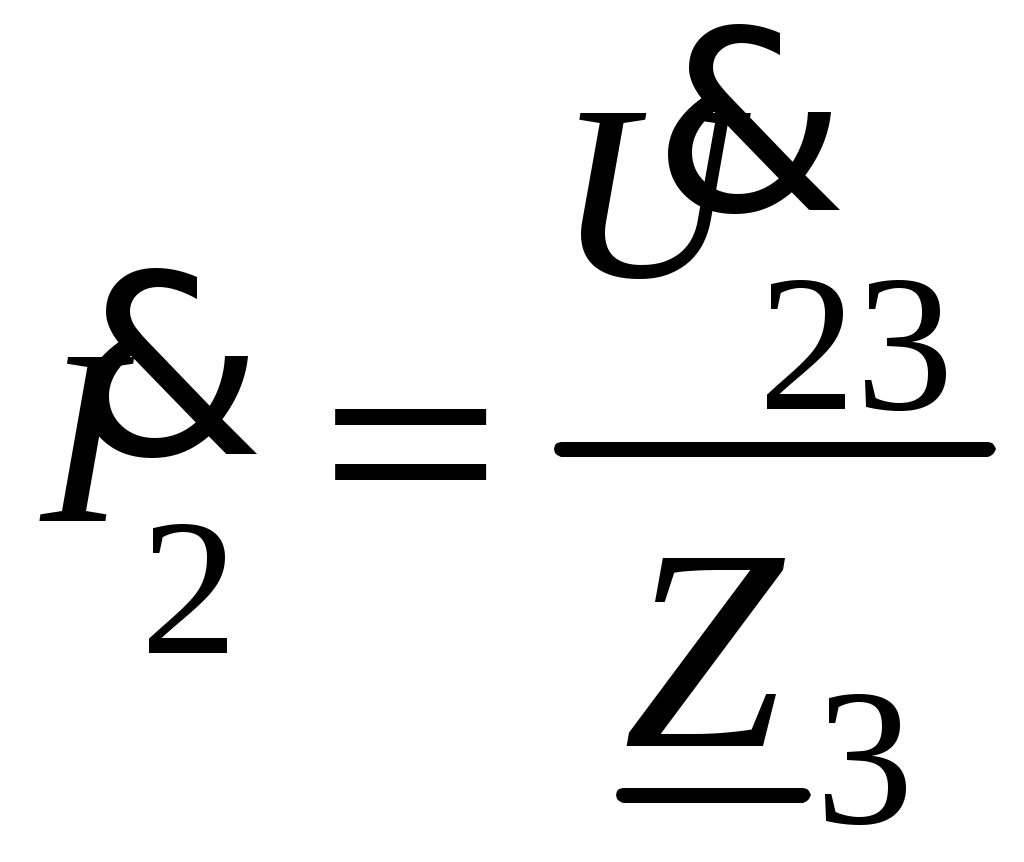 .
.
Проверка решения осуществляется по первому закону Кирхгофа для одного из узлов цепи. Например, для узла a имеем:
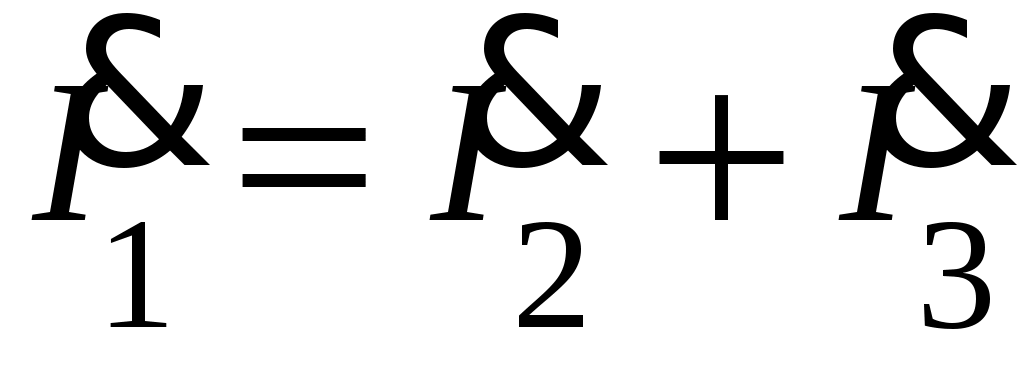 .
.
Если расчет произведен верно, то сумма комплексных токов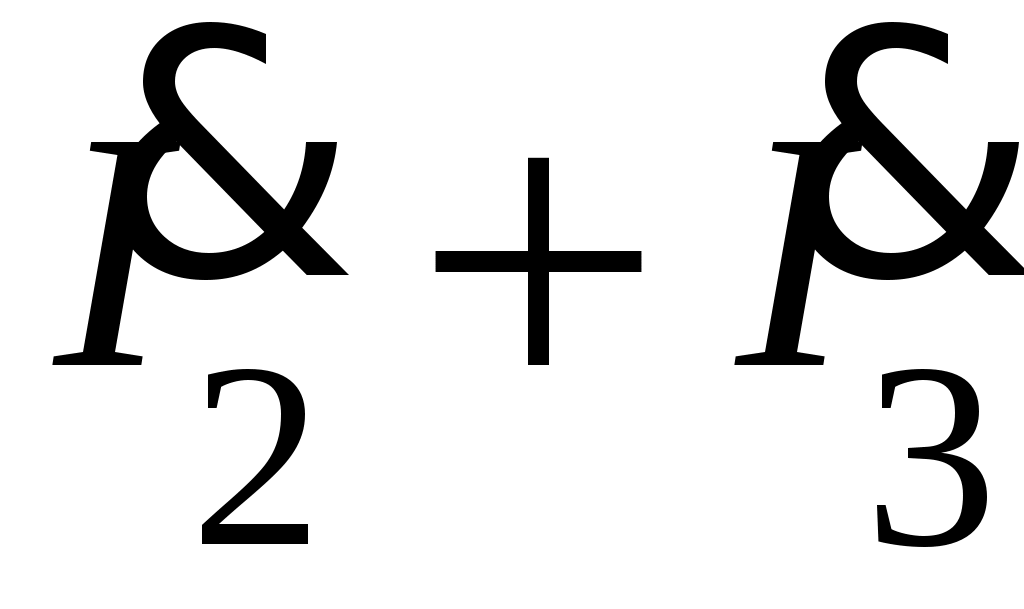 должна быть практически равна комплексному току
должна быть практически равна комплексному току 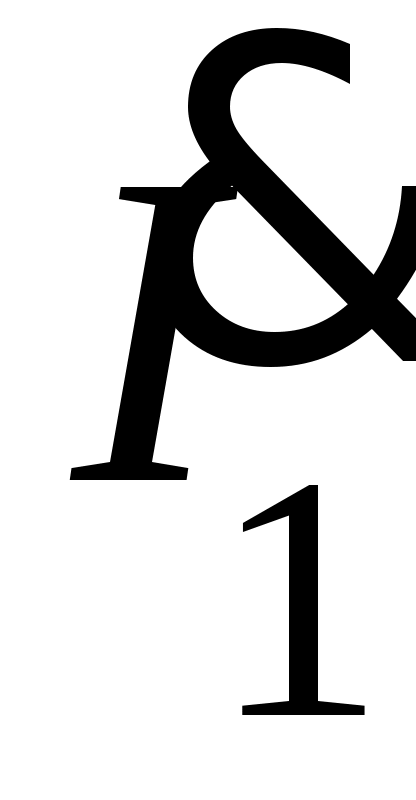 .
.
Порядок расчета цепи с параллельно-последовательным
соединением комплексных сопротивлений (рис. 3.1, б)
1. Определяется эквивалентная комплексная проводимость всей цепи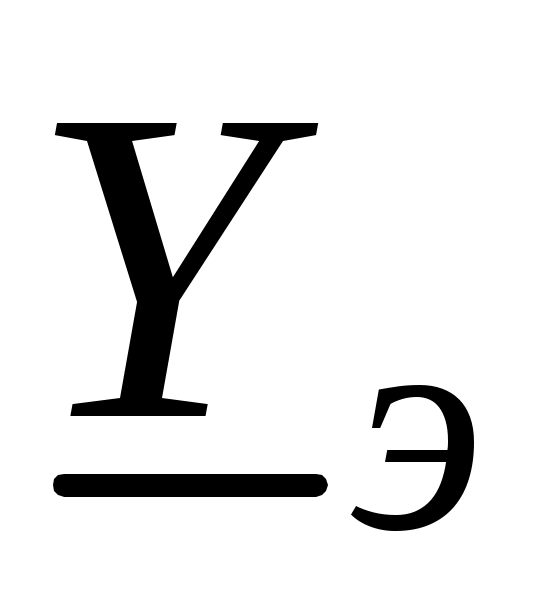
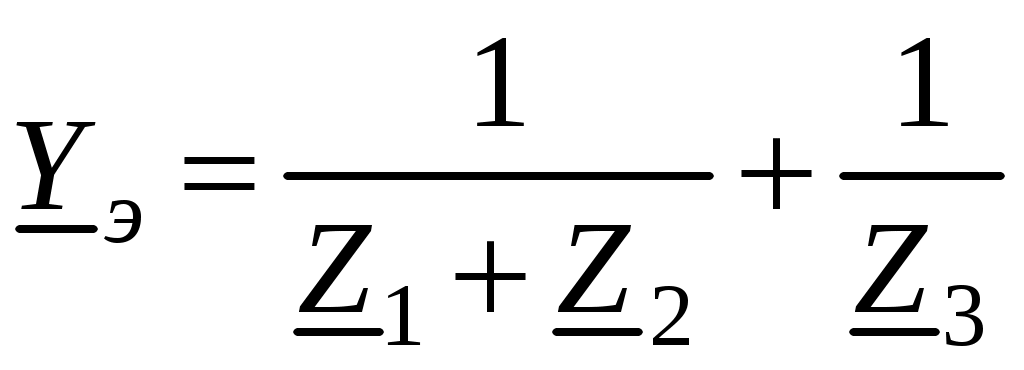 .
.
2. Определяется комплексное действующее значение тока цепи
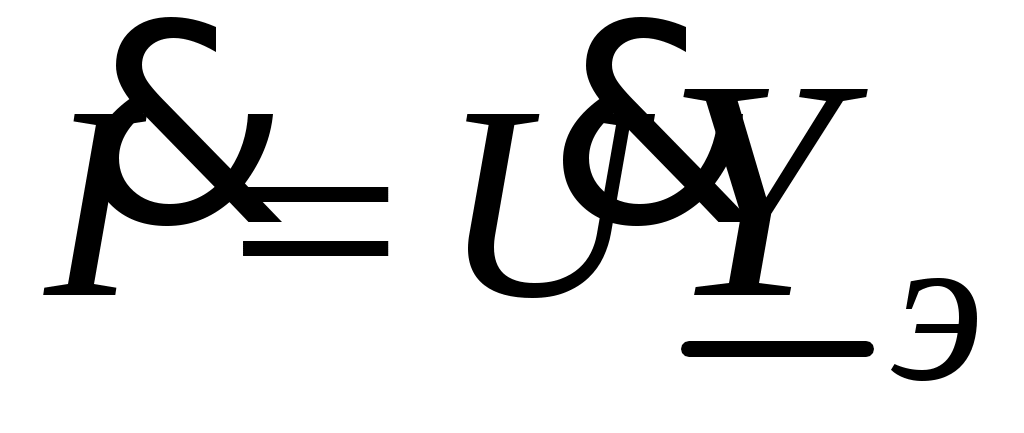 .
.
Начальную фазу приложенного напряжения можно принять равной нулю, т. е. .
.
3. Определяется комплексное действующее значение тока
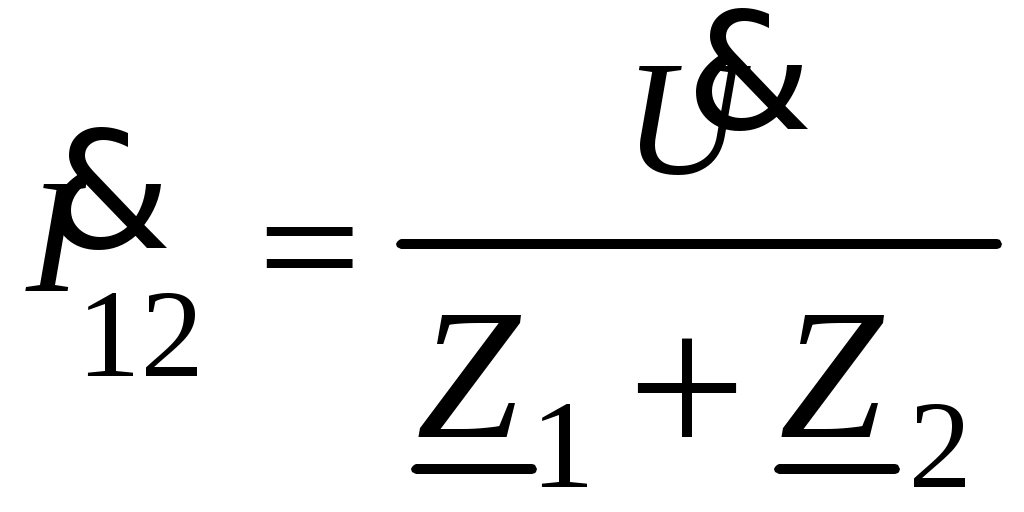 .
.
4. Определяется комплексное действующее значение напряжения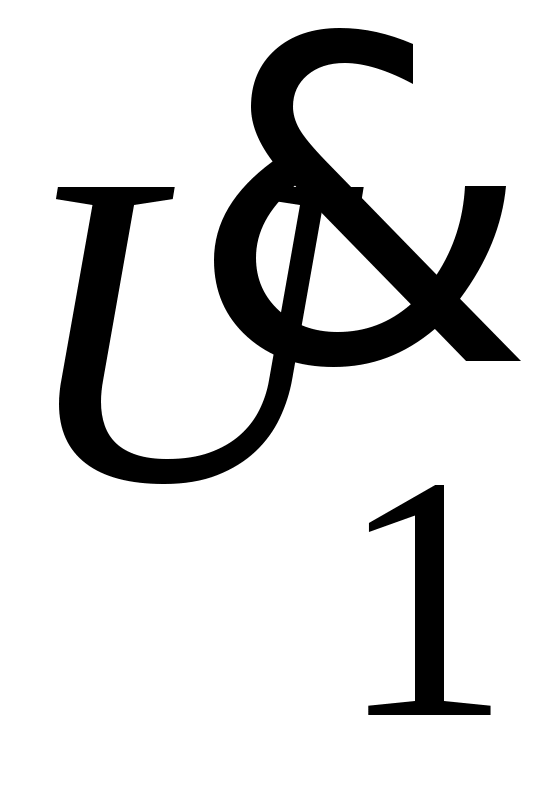
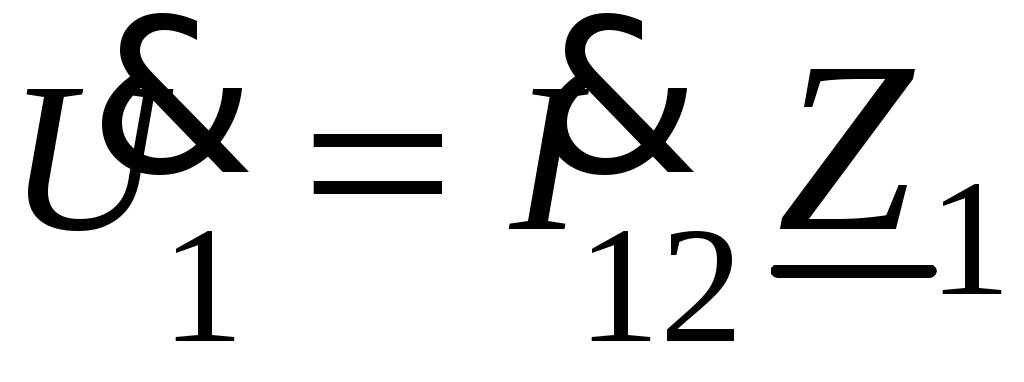 .
.
5. Определяется комплексное действующее значение напряжения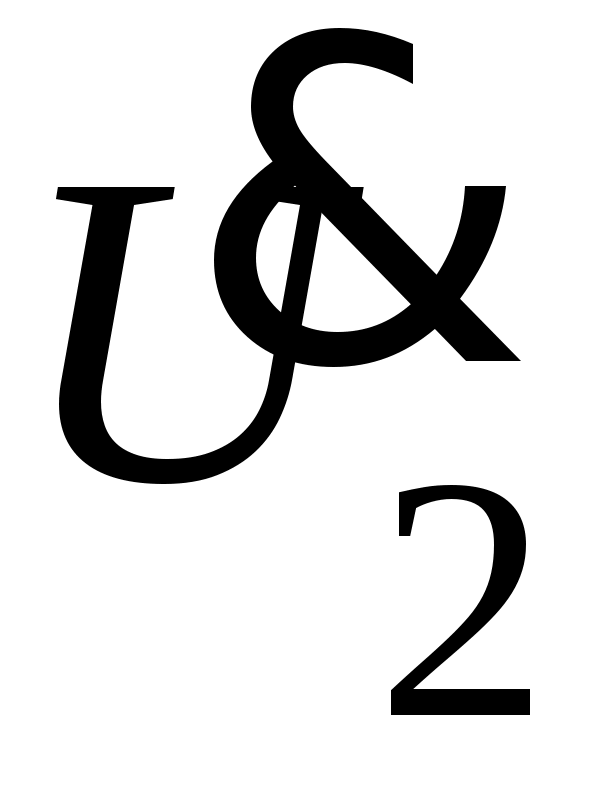
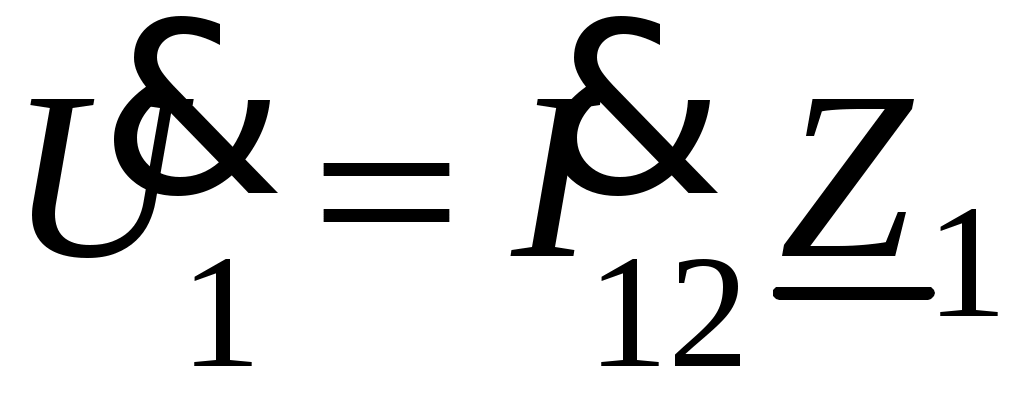 .
.
6. Определяется комплексное действующее значение тока
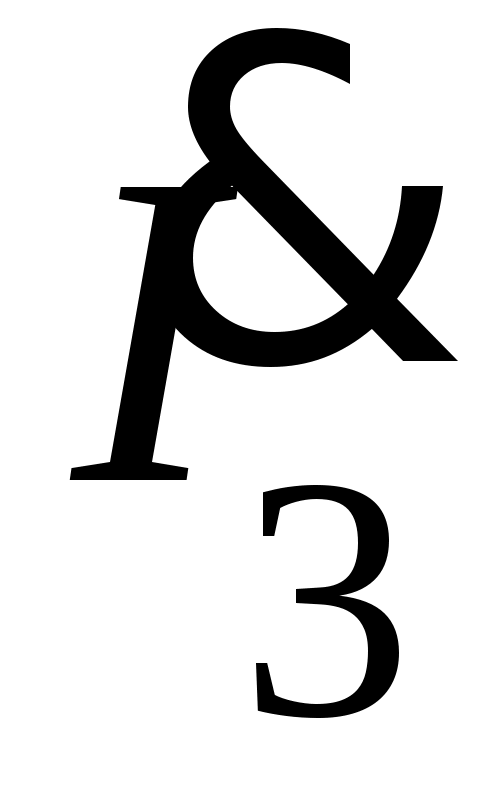
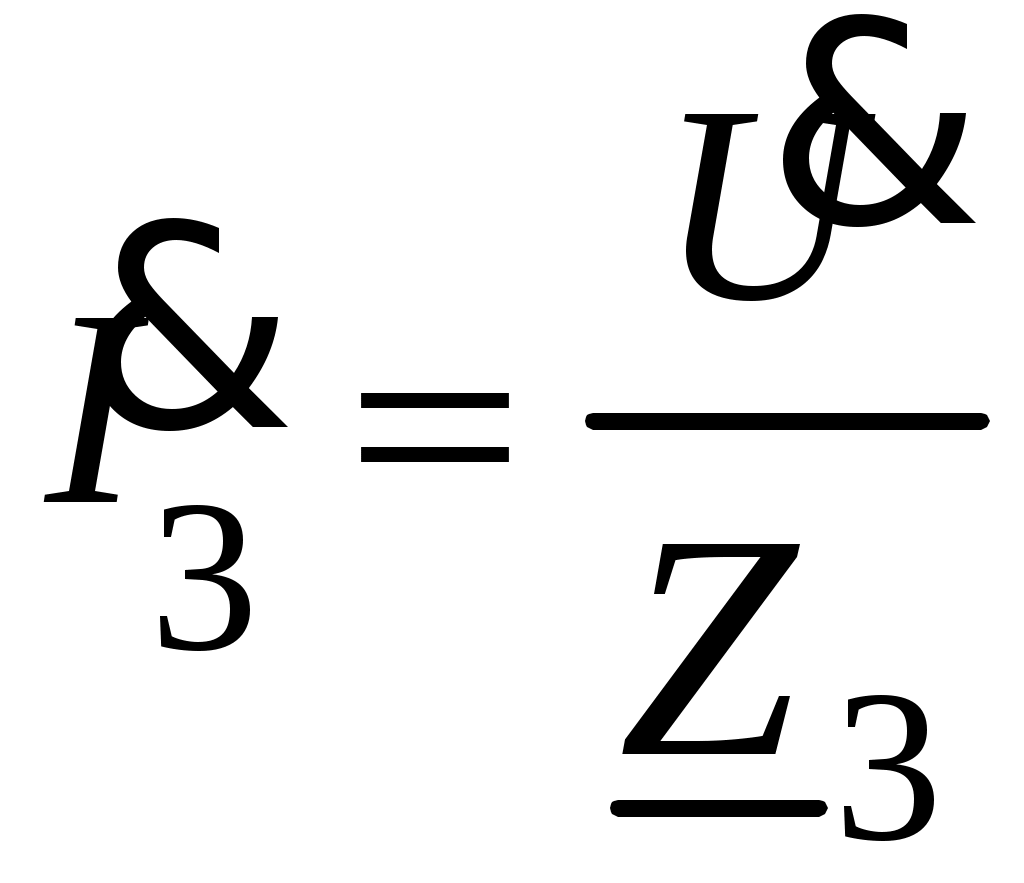 .
.
Проверка решения осуществляется по первому закону Кирхгофа для одного из узлов цепи или по второму закону Кирхгофа для одного из контуров цепи. Например, для узла а имеем: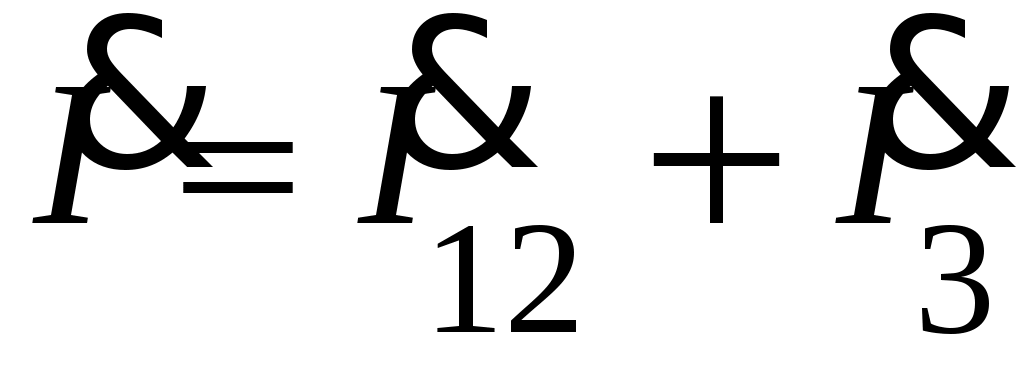 ; для левого контура (на схеме рис. 3.1, б указано направление его обхода) имеем:
; для левого контура (на схеме рис. 3.1, б указано направление его обхода) имеем: 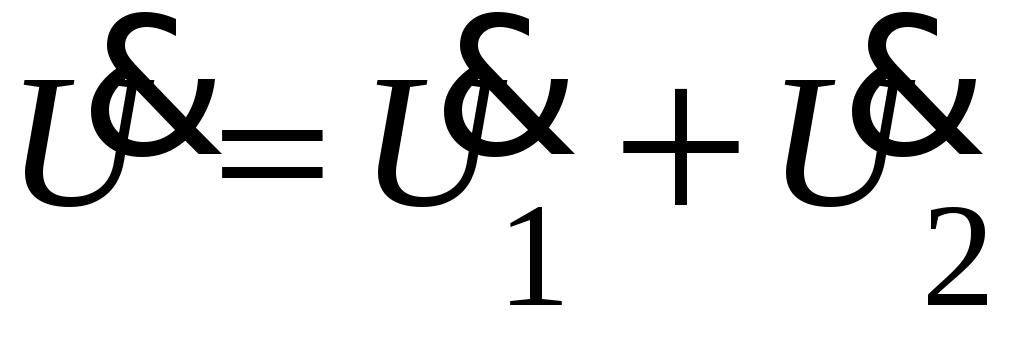 .
.
Если расчет произведен верно, то сумма комплексных токов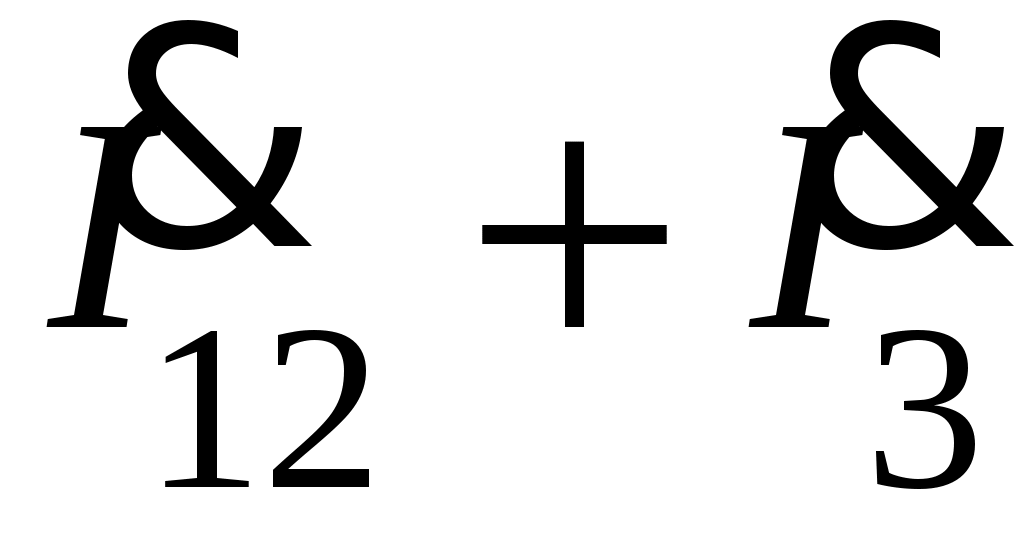 должна быть практически равна комплексному току
должна быть практически равна комплексному току 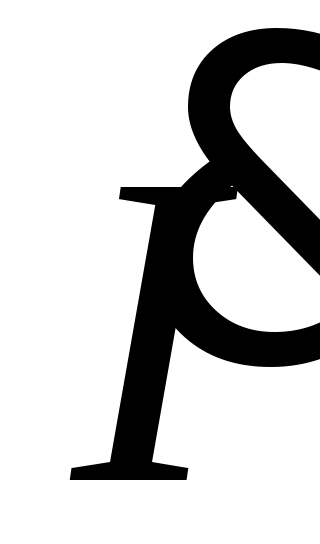 , а сумма комплексных напряжений
, а сумма комплексных напряжений 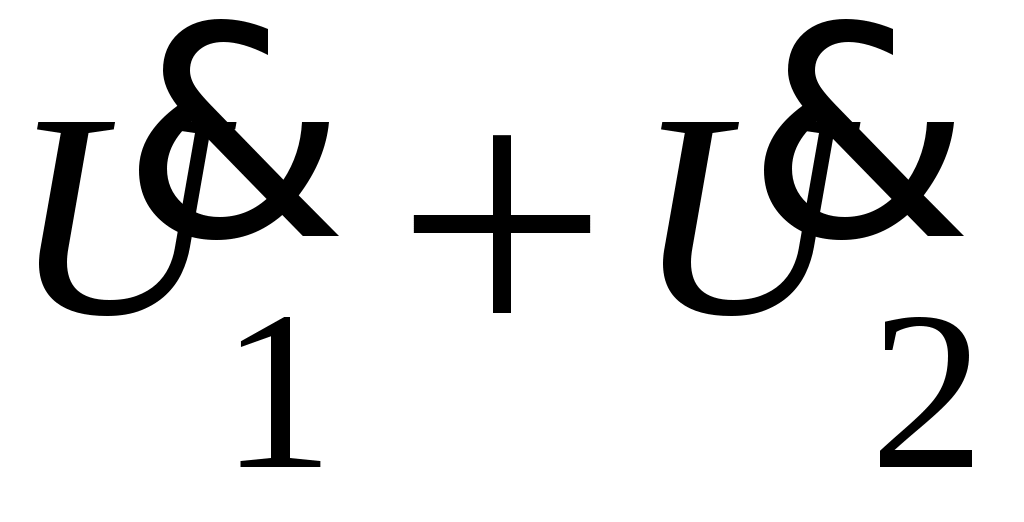 должна быть практически равна комплексному напряжению цепи
должна быть практически равна комплексному напряжению цепи  .
.
Описание элементов исследуемой цепи
В качестве элементов исследуемой цепи применяются резисторы, катушки индуктивности и конденсаторы, которые в диапазоне используемых частот принимаются идеализированными элементами цепи, т. е. полагают, что резистор обладает только сопротивлением R, катушка индуктивности обладает только индуктивностью L и конденсатор обладает только емкостью C.
Комплексные сопротивления таких элементов записываются следующим образом:
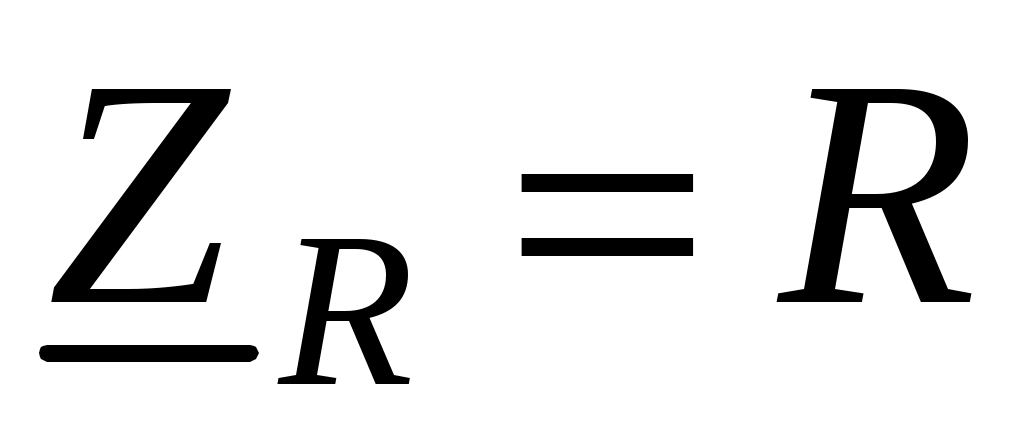 ,
, 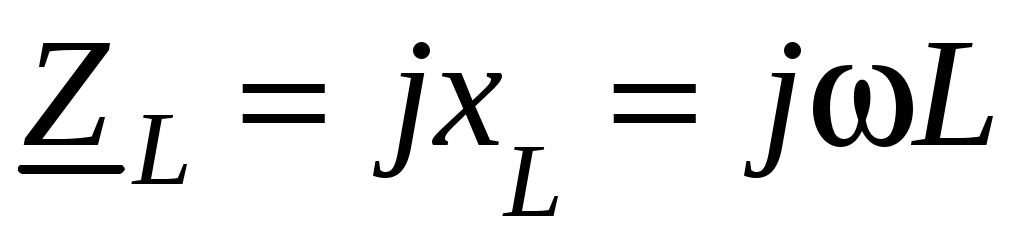 ,
, 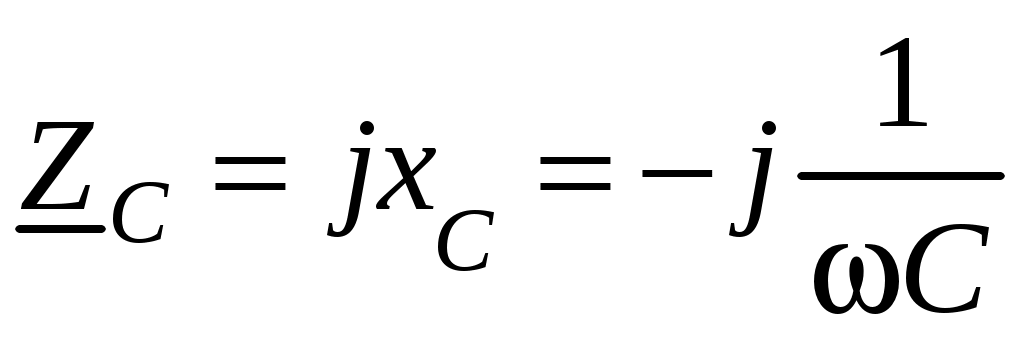 .
.
В данной работе студенты исследуют одну из цепей, составленных из комбинации идеализированных элементов ZR , ZL, ZC (рис. 3.2, а). Векторные диаграммы (рис. 3.2, б) для этих цепей приведены в общем виде (без масштабов).
Экспериментальное исследование параметров цепи
Для экспериментального определения параметра любого идеализиро-
3. Основные расчетные соотношения.
4. Таблица по форме 2.1 с результатами измерений и вычислений.
5. Краткие выводы.
5. ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Чем отличаются идеализированные элементы электрической цепи от реальных элементов?
2. Почему в данной работе в качестве идеализированных элементов можно использовать резистор, катушку индуктивности и конденсатор?
3. Для некоторой цепи известны напряжение и ток:
Требуется определить:
действующие значения напряжения и тока цепи;
частоту цепи f, Гц;
угол сдвига фаз между напряжением и током цепи;
характер цепи индуктивной или емкостной.
Построить графики зависимости тока и напряжения цепи от времени.
Построить векторную диаграмму цепи.
4. В цепи с активным сопротивлением измерены действующие значения тока и напряжения I = 1A; U = 10 B. Требуется определить величину активного сопротивления.
Записать ток и напряжение в виде синусоид, если частота цепи
f = 1000 Гц, а начальная фаза напряжения u = 60. Построить графики зависимости тока и напряжения от времени. Построить векторную диаграмму цепи.
5. В цепи с индуктивностью измерены действующие значения тока и напряжения U =10 B, I = 1A. Требуется:
определить величину индуктивного сопротивления xL;
определить величину индуктивности L, если частота цепи f =1590 Гц;
записать ток и напряжение в виде синусоид, если частота цепи
f = 1590 Гц, а начальная фаза напряжения u = 360;
построить векторную диаграмму цепи.
6. В цепи с емкостью измерены действующие значения тока и напряжения цепи: U = 10 B; I = 1 A. Требуется:
определить величину индуктивного сопротивления xС;
определить величину индуктивности С, если частота цепи f = 1590 Гц;
записать ток и напряжение в виде синусоид, если частота цепи
f =1590 Гц, а начальная фаза напряжения u = 60;
построить векторную диаграмму цепи.
7. Как зависят активное сопротивление R, индуктивное сопротивление xL, и емкостное сопротивление xС от частоты приложенного напряжения?
8. Индуктивное сопротивление цепи составляет 8 Ом. Как изменится это сопротивление, если частоту приложенного напряжения увеличить в два раза?
Л и т е р а т у р а: [2], c. 19...29.
Работа 3. ИССЛЕДОВАНИЕ РАЗВЕТВЛЕННОЙ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА С ОДНИМ ИСТОЧНИКОМ ЭНЕРГИИ
1. ЦЕЛЬ РАБОТЫ
Экспериментальное исследование разветвленной электрической цепи с одним источником синусоидального напряжения и ее расчет комплексным методом.
2. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
В данной работе исследуется цепь, со смешанным соединением трех комплексных сопротивлений Z1, Z2 и Z3. Рассматривается одна из двух схем такой цепи: с последовательно-параллельным (рис. 3.1, а) и параллельно-последовательным (рис. 3.1, б) соединениями этих элементов.

Рис. 3.1
Расчет исследуемой цепи
Задача расчета состоит в определении токов во всех ветвях цепи при известных параметрах, заданном действующем значении приложенного к цепи напряжения и частоте сети. Расчет производится символическим методом (методом комплексных амплитуд) с использованием преобразований цепи либо к последовательному, либо к параллельному соединению ее элементов.
Порядок расчета цепи с последовательно-параллельным
соединением комплексных сопротивлений (рис. 3.1, а)
1. Определяется эквивалентное комплексное сопротивление цепи Zэ
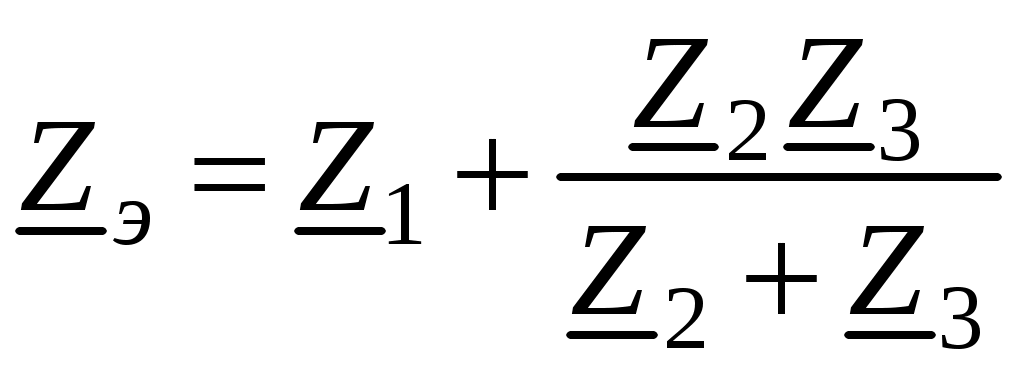 .
.2. Определяется комплексное действующее значение тока
При этом начальная фаза приложенного напряжения может быть принята равной нулю, т. е.
3. Определяется комплексное действующее значение напряжения на участке цепи с параллельным соединением Z2 и Z3
4. Определяется комплексное действующее значение тока
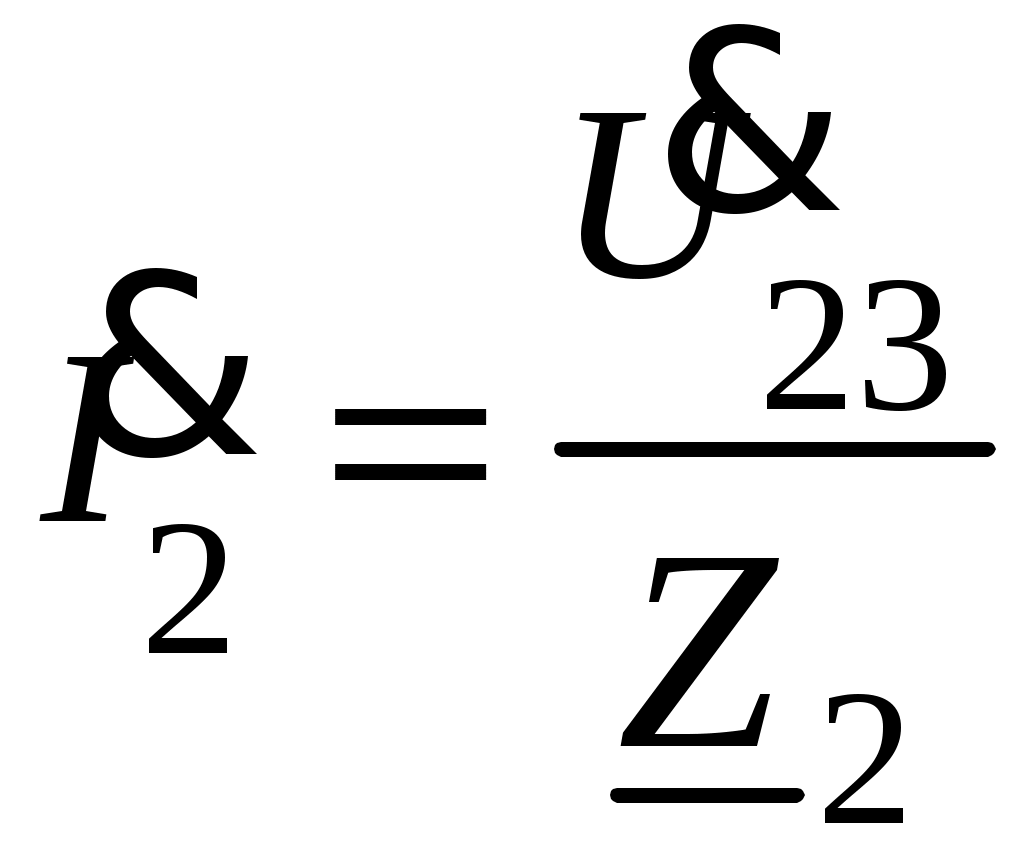 .
.5. Определяется комплексное действующее значение тока
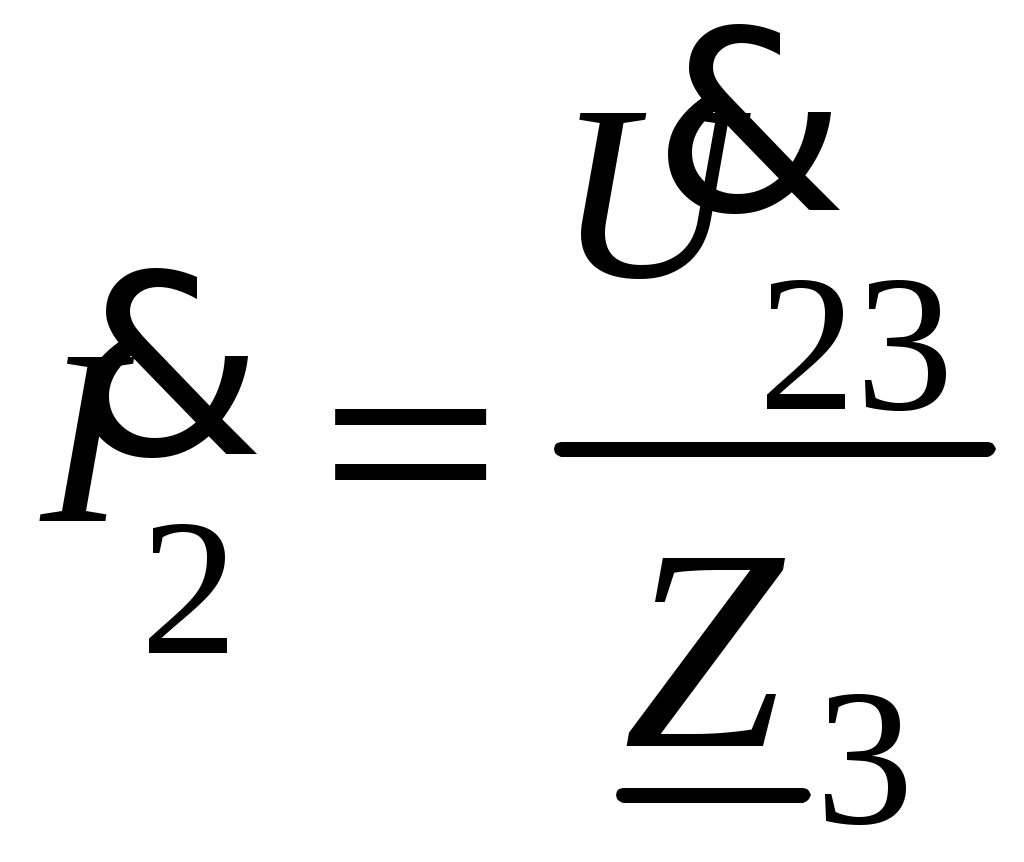 .
.Проверка решения осуществляется по первому закону Кирхгофа для одного из узлов цепи. Например, для узла a имеем:
Если расчет произведен верно, то сумма комплексных токов
Порядок расчета цепи с параллельно-последовательным
соединением комплексных сопротивлений (рис. 3.1, б)
1. Определяется эквивалентная комплексная проводимость всей цепи
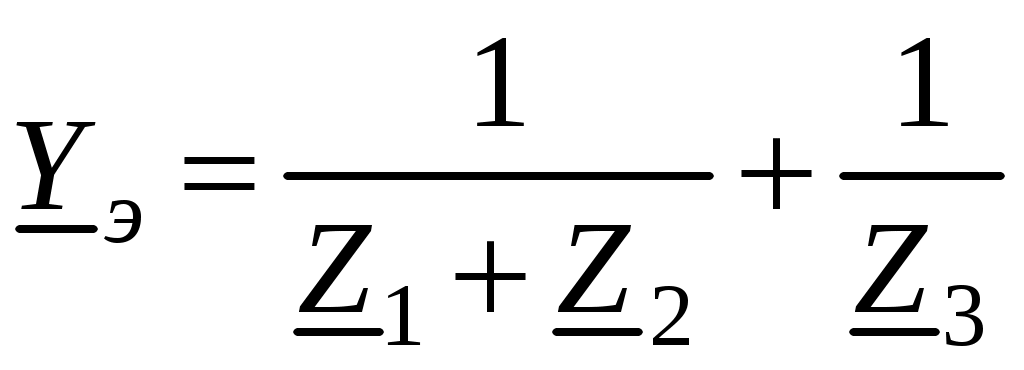 .
.2. Определяется комплексное действующее значение тока цепи
Начальную фазу приложенного напряжения можно принять равной нулю, т. е.
3. Определяется комплексное действующее значение тока
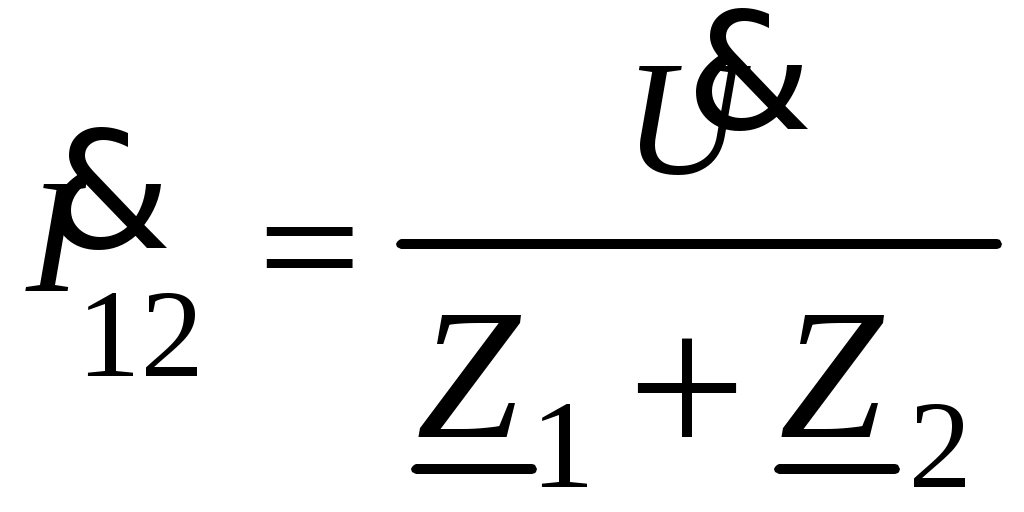 .
.4. Определяется комплексное действующее значение напряжения
5. Определяется комплексное действующее значение напряжения
6. Определяется комплексное действующее значение тока
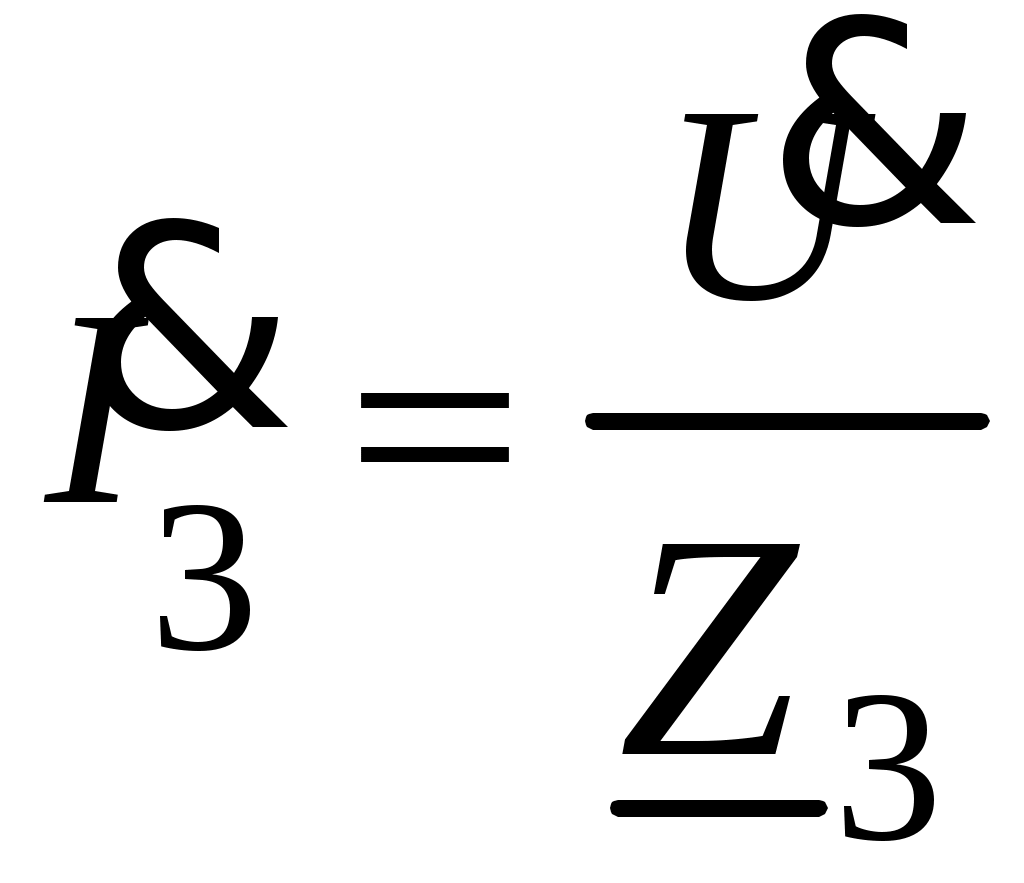 .
.Проверка решения осуществляется по первому закону Кирхгофа для одного из узлов цепи или по второму закону Кирхгофа для одного из контуров цепи. Например, для узла а имеем:
Если расчет произведен верно, то сумма комплексных токов
Описание элементов исследуемой цепи
В качестве элементов исследуемой цепи применяются резисторы, катушки индуктивности и конденсаторы, которые в диапазоне используемых частот принимаются идеализированными элементами цепи, т. е. полагают, что резистор обладает только сопротивлением R, катушка индуктивности обладает только индуктивностью L и конденсатор обладает только емкостью C.
Комплексные сопротивления таких элементов записываются следующим образом:
В данной работе студенты исследуют одну из цепей, составленных из комбинации идеализированных элементов ZR , ZL, ZC (рис. 3.2, а). Векторные диаграммы (рис. 3.2, б) для этих цепей приведены в общем виде (без масштабов).
Экспериментальное исследование параметров цепи
Для экспериментального определения параметра любого идеализиро-

