Для иллюстрации конструкции "цикл пока" можно привести следующую модификацию алгоритма проезда.

 

алгоритм Добраться из Аэровокзала до Домодедово

| Дано: находимся у Аэровокзала

| Надо: оказаться в аэропорту Домодедово

начало алгоритма

|

| цикл пока пробка на Ленинградском проспекте

| | выпить чашку кофе в кафе Аэровокзала

| | ждать полчаса

| конец цикла

|

| Проезд от аэровокзала до Домодедово через МКАД

конец алгоритма

 

Здесь снова использован определенный ранее алгоритм "Проезд от аэровокзала до Домодедово". Условие продолжения цикла проверяется перед выполнением тела цикла, но не в процессе его выполнения! Так, если пробка рассосалась после чашки кофе, то все равно нужно ждать полчаса.

Теперь можно подвести итоги.

Запись алгоритма на неформальном языке представляет собой последовательность команд исполнителю алгоритма. Запись может также включать управляющие конструкции: ветвление, или условный оператор, и цикл "пока". Условный оператор выглядит следующим образом:

 

если условие

| то

|   последовательность действий 1

| иначе

|   последовательность действий 2

конец если

 

Последовательность действий 1 выполняется, когда условие истинно; в противном случае выполняется последовательность действий 2. Ключевое слово "иначе" и последовательность действий 2 могут отсутствовать; в этом случае, когда условие ложно, исполнитель ничего не делает.

Цикл "пока", или цикл с предусловием выглядит следующим образом:

 

цикл пока условие

| последовательность действий

конец цикла

 

Сначала проверяется условие в заголовке цикла. Если оно истинно, то выполняется последовательность действий, составляющая тело цикла. Это повторяется неограниченное число раз, пока условие истинно. Цикл заканчивается, когда условие при очередной проверке оказывается ложным. Важно отметить, что условие проверяется перед каждым выполнением тела цикла, но не в процессе его выполнения.

Помимо элементарных действий, в записи алгоритма можно использовать другие алгоритмы. Также в записи алгоритма могут присутствовать комментарии, которые игнорируются исполнителем алгоритма. Для отделения комментария будут использоваться знаки // (двойная косая черта) для строчного комментария или /* …. */ для блока в соответствии с синтаксисом языка C++.

---

 

3.3. Язык схем

 

Схемой называется наглядное графическое изображение алгоритма, когда отдельные действия (этапы) алгоритма изображаются при помощи различных геометрических фигур (блоков), а связи между этапами (последовательность выполнения этапов) указываются при помощи линий, соединяющих эти фигуры.

Несмотря на все многообразие решаемых на ЭВМ задач, можно выделить несколько «типичных» действий (этапов), которые в различной последовательности выполняются при решении задач:

1.Присваивание является основной операцией, при помощи которой осуществляется обработка данных.

2.Проверка условия и выбор в зависимости от результата проверки одного из двух путей вычислительного процесса.

3.Ввод данных и вывод результата.

4.Начало и конец вычислительного процесса.

 

Конкретные операции указаны внутри фигур в качестве примеров. Рассмотрим выполнение этих действий, а также функции других элементов схем, приведенных на рис.4.1.

 

 

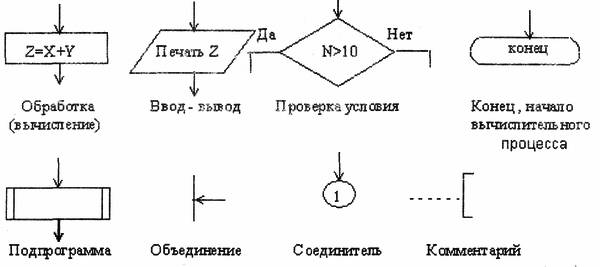
Рис. 4.1. основные элементы схем

 

Присваивание. При выполнении операции присваивания переменной присваивается значение (переменная – некоторая величина, которая может изменяться, принимая в процессе этого изменения различные значения). Переменная обозначается при помощи имени. Именами обозначаются также различные функции (например, SIN). Функции имеют, в языках программирования, закрепленные за ними имена. Как Вы уже знаете, имя переменной обозначает символический адрес той ячейки памяти, в которой записано числовое значение соответствующей переменной или функции (после ее вычисления). Следовательно, термины "переменная" или "функция" только условно соответствуют общепринятым математическим понятиям. Числа, используемые, например, в операторах присваивания для задания значений переменных, называются константами. Константы обозначают сами числа, а не 

---

фактические адреса ячеек памяти.

Оператор присваивания, обсуждающийся в этом разделе, используется только для выполнения арифметических операций, поэтому он называется арифметическим оператором присваивания. В языках программирования имеются и другие виды операторов присваивания. Арифметический оператор присваивания выполняет следующие действия.

Операции, указанные справа от символа "=", выполняются над записанными в выражении константами (константа- величина, значение которой не изменяется в период ее существования) и теми числами, которые хранятся в ячейках памяти, обозначенных встречающимися именами. Результат помешается в ту ячейку памяти, символический адрес которой указан слева от символа "=". Говорят, что переменной присваивается значение посредством оператора присваивания. Следовательно, используемый здесь символ "=" (присвоить) имеет смысл, отличный от принятого в математике.

 

Примеры операторов присваивания

 

Оператор присваивания    Действие оператора

К=1           В ячейку памяти с символическим адресом К помещается 1. (переменной К присваивается значение 1)

L=K           В ячейку памяти с символическим адресом L пересылается содержимое ячейки с символическим адресом К (переменной L присваивается значение К). При этом К не изменяется.

К=К+1        К содержимому ячейки с символическим адресом К прибавляется 1, результат помещается в ту же ячейку К. При этом старое значение К пропадает (стирается).

Y=SIN(X) Вычисляется sin угла (выраженного в радианах), величина которого находится в ячейке X, и результат помещается в ячейку Y.

X=SIN(X) Правая часть вычисляется аналогично. Значение функции записывается в ту же ячейку, в которой раньше находилось значение угла. Перед присваиванием старое значение пропадает (стирается).

 

Замечания:

1. Перед выполнением присваивания старое значение переменной стирается.

2. При пересылке значение переменной копируется. Значение копируемой переменной не изменяется.

3. Переменным,  которые располагаются в  правой части оператора присваивания, должны  быть присвоены определенные значения предшествующими операторами.

---

4. Если переменной не присвоено значение, то ее значение не определено.

Проверка условия. Проверка условия является основой организации разветвлений, т. е. выбора одного из двух (или более) путей вычислительного процесса. Это этап принятия решения о дальнейшем ходе вычислительного процесса в зависимости от полученных промежуточных результатов. Имеется три вида разветвлений (см. ниже).

Ввод-вывод данных. В операторах ввода-вывода записываются имена тех переменных, значения которых должны вводиться в оперативную память или выводиться из нее. В этих операторах могут быть указаны также внешние устройства, с которыми осуществляется обмен информацией. При вводе данные записываются в те ячейки памяти, символические адреса (имена) которых указаны в операторе. При выводе (печати) данных на экране (или бумаге) появляются значения, находящиеся в ячейках памяти, символические адреса которых перечислены в операторе вывода.

Подпрограмма. Группу операторов, которые решают логически самостоятельную часть задачи, можно объединить в подпрограмму.

Соединительные линии и их объединение. Все блоки схемы соединяются посредством линий, которые в сомнительных случаях снабжаются направляющими стрелками. Основными являются направления сверху вниз и слева направо. Объединение нескольких ветвей в одну ветвь обозначается точкой. Пересекающиеся линии без обозначения точки пересечения означают отсутствие соединений, по возможности следует избегать пересечений.

Точками связи, или соединителями, пользуются в том случае, если соединительная линия не может быть доведена до следующего блока или до точки объединения. Тогда линия оканчивается соединителем, в котором записывается любой символ. Продолжением этой линии считается вторая точка связи, помеченная тем же символом.

Комментарии можно записывать около любого блока.

Содержание блоков не стандартизировано и зависит от степени детализации алгоритма. В частности, прямоугольник может быть использован для обозначения не только одной операции присваивания, но и более емких этапов преобразования (обработки) данных. Важно только, чтобы этот этап имел одного преемника, т. е. – чтобы после него выполнялся всегда один и тот же блок. При решении сложных задач обычно составляют несколько схем с различным уровнем детализации. Схема на каждом этапе разработки алгоритма должна давать наглядное представление об общей структуре алгоритма в целом или отдельных его частей.

---

Схема не должна быть громоздкой, так как это приводит к потере наглядности, являющейся основным преимуществом схем, и не должна дублировать программу, изображая каждый оператор в виде отдельного блока. Последнее не относится к начинающим программистам. В частности, в настоящем пособии из дидактических соображений приводятся достаточно подробные схемы.

 

3.4. Основные структуры алгоритмов

 

Основные структуры алгоритмов — это ограниченный набор стандартных способов соединения отдельных блоков или структур для выполнения типичных последовательностей действий.

Приводимые ниже структуры рекомендуются при использовании так называемого структурного подхода к разработке алгоритмов и программ. Структурный подход предполагает использование только нескольких основных структур, комбинация которых дает все многообразие алгоритмов и программ.

К основным структурам относятся (см. рис. 4.2):

  следование а;

  две разновидности цикла б, в;

  три разновидности разветвления г, д, е.

 

 

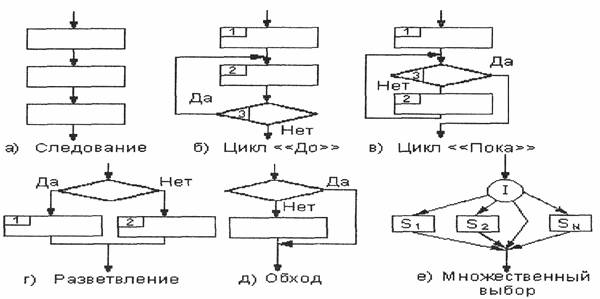
Рис.4.2. Основные структуры алгоритмов.

 

Отметим вначале особенности трех основных типов структур.

Следование – это последовательное размещение блоков и групп блоков, такая структура называется также линейной.

Если некоторая часть программы (на схеме группа блоков) выполняется многократно и после проверки некоторого условия в какой-то момент осуществляется выход из нее, то такую часть называют циклом.

Если после проверки некоторого условия выбирается один из двух (или более) путей вычислительного процесса и после выполнения любого из них вычислительный процесс опять сводится в одно русло, то возникает разветвление.

Теперь рассмотрим особенности каждого вида цикла и разветвления.

Цикл До. Применяется при необходимости выполнить какие-либо вычисления нескольких раз до выполнения некоторого условия (блок 3). Особенность этого цикла в том, что он всегда выполняется хотя бы один раз, так как первая проверка условия выхода из цикла происходит после того, как тело цикла выполнено. 

---

Смотрите также файлы

• Установленный лимит остатка денежных средств в кассе 3000 рублей. Остаток в кассе на начало дня 2500 рублей.docx

• Гносеология (эпистемология).pdf

• Оптимизационные модели экономического роста.docx

• дістсіл трі.doc

• Система контроля качества в строительстве при производстве земляных работ.rtf