Файл: Решение. Введем в рассмотрение следующие события a получили слово река.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 04.05.2024

Просмотров: 9

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Автономная некоммерческая организация высшего образования

«МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра экономики и управления
Форма обучения: заочная/очно-заочная


ВЫПОЛНЕНИЕ

ПРАКТИЧЕСКИХ ЗАДАНИЙ

ПО ДИСЦИПЛИНЕ

Теория вероятностей и математическая статистика



Группа Чн20Э271

Студент
Е.И. Башилова


МОСКВА 2021
Задание 1. Буквы, составляющие слово РАКЕТА, написаны по од­ной на шести карточках; карточки перемешаны и положены в пакет, а) Чему равна вероятность того, что, вынимая четыре буквы, получим слово РЕКА? б) Какова вероятность сложить слово КАРЕТА при выни­мании всех букв?

Решение.

Введем в рассмотрение следующие события:
A={получили слово РЕКА}, B={получили слово КАРЕТА}.
Используя теорему умножения вероятности, получим:

P(A)=
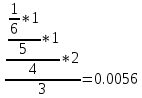
P(B)=
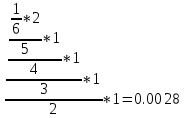
Ответ: 1) 0.0056; 2) 0.0028.

Задание 2. Дискретная случайная величина ξ задана следующим законом распределения:


ξ

4

6

10

12


р

0.4

0.1

0.2

0.3


Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.
Решение. Найдем заданные числовые характеристики:

M|ξ|=4*0.4+6*0.1+10*0.2+12*0.3=7.8
D|ξ|=16*0.4+36*0.1+100*0.2+144*0.3-7.82=12.36
Q|ξ|=√D|ξ|=√12.36=3.516
Ответ: M|ξ|=7.8, D|ξ|=12.36, Q|ξ|=3.516  
Задание 3. Возможные значения дискретной случайной величи­ны равны:-2, 1, 4. При условии, что заданы математическое ожидание M|ξ|=1.9 , а также M|ξ2|=7.3 , найти вероятности P1,P2,P3  которые соответствуют дискретным значениям случайной величины.

Решение. Так как:   ,   и   , то получим:

 .

Найдем решение системы методом Гаусса:

 .

Ранг матрицы системы равен рангу расширенной матрицы, значит, система совместна. Тогда получим:

 , тогда   .

 , тогда   .

 , тогда   .

Ответ:   ,   ,   .

Смотрите также файлы