Файл: Последовательность действий для решения задач с применением принципа Дирихле.docx
Добавлен: 05.05.2024
Просмотров: 24
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Приложение1
Рис.1.
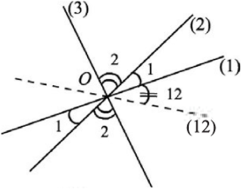
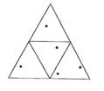 рис.2
рис.2.
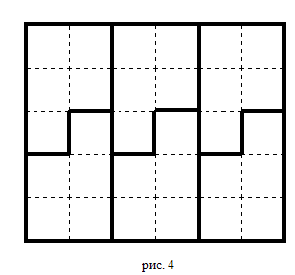
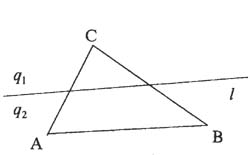
Рис.3.
Таблица 1.Последовательность действий для решения задач с применением принципа Дирихле.
| Последовательность действий | Пример выполнения |
| 1.Определить, что в данной задаче удобно принять за «клетки», а что за «зайцев». | Каждая грань куба раскрашена в черный или белый цвет. Докажите, что найдутся две одинаково раскрашенные грани, имеющие одно ребро. Принимаем за «клетки» - цвета, а за «кроликов» грани, пересекающиеся в одной вершине. |
| 2. При необходимости преобразовать условия задачи в удобный для понимания вид и получить «клетки» и «зайцев». | Данная задача в преобразованиях не нуждается. |
| 3. Выбрать для решения задачи удобную формулировку принципа Дирихле. | Для решения данной задачи выбираем следующую формулировку: «если в n клетках сидит n + 1 зайцев или больше зайцев, то найдётся клетка, в которой сидят по крайней мере два зайца». |
| Привести условия задачи к выбранной формулировке принципа Дирихле. | «клеток» получилось две, по принципу Дирихле из этого следует, что зайцев будет 2+1 = 3. Так как у нас получилось 3 грани, а цвета всего 2, из этого следует, что какие-то две грани будут одинаково раскрашены. |
| 5. Получаем ответ или результат доказательства. | Задача доказана. |
Приложение 2
Задача №1 В магазин привезли 25 ящиков с яблоками трех сортов
, причем в каждом ящике лежат яблоки какого-то одного сорта. Можно ли найти 9 ящиков с яблоками одного сорта?Решение: 25 ящиков – «кроликов» рассадили по трем «клеткам». Так как 25 = 3* 8+1, то применим обобщенный принцип Дирихле для N = 3, k = 8 и получим, что в какой-то «клетке» - сорте не менее 9 ящиков.Ответ: Можно
Задача № 2 Верно ли, что из шести любых целых чисел найдутся два числа, разность которых делится на 5?
Решение: Шесть чисел – зайцы, клетки – остатки от деления чисел на 5: 0, 1, 2, 3, 4, значит, найдется клетка, в которой будут сидеть 2 зайца – числа с равными остатками от деления их на 5. Тогда и разность этих чисел делится на 5.
(26:5 = 5*5+1; 16:5=3*5+1; 26 – 16 = 10, 10
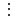 5)
5)Задача №3На шахматной доске размером 8х8 Вася расставил 14 фигур. Докажите, что найдется квадрат размером 2х2, в котором не будет фигур. (Фигуры размещаются внутри клеток размером 1х1).Решение: Разобьем квадрат 8х8 на 16 клеток.
Тогда получаем 16 «клеток» и 14 «зайцев» - фигур. Так как 16>14, то найдется как минимум одна клетка, которая будет пустой.
Задача №6 В мешке лежат 10 белых и 10 черных шаров. Они тщательно перемешаны и неразличимы на ощупь. Какое наименьшее число шаров нужно вынуть из мешка вслепую, чтобы среди них наверняка оказались два шара 1) одного цвета, 2) разного цвета, 3) белого цвета? Решение: 1) Цвета шаров обозначим за «клетки» (их две), значит «зайцев» надо больше. Достанем из мешка 3 шара. Так как 3>2 , то по принципу Дирихле найдется «клетка» (цвет шара), в которую попадут как минимум 2 «зайца» (шара). Значит, надо достать наименьшее число шаров – 3.
2) Так как подряд могут попадаться все время шары одного цвета, то надо достать наименьшее число шаров – 11
3) наименьшее число шаров будет 12
Задача №4:Внутри правильного шестиугольника со стороной 1см расположено 7 точек. Докажите, что расстояние между двумя точками меньше, чем 1см.
Док-во: Примем 7 точек за зайцев. Построим 6 клеток. Для этого разобьем правильный шестиугольник на 6 правильных треугольников, как на рисунке. Так как 7>6, то по принципу Дирихле хотя бы в один треугольник попадут не менее 2 точек. А расстояние между любыми 2 точками в правильном треугольнике со стороной 1см меньше 1см
Задача 5. Шахматная доска разрезана на 13 прямоугольников с целым числом клеток. Могут ли они все быть различными? Найдутся ли два равных прямоугольника? Решение. Допустим, что все 13 прямоугольников попарно неравны. Минимальная их площадь (1×1, 1×2, …, 1×8, 2×2, 2×3, 2×4, 2×5, 3×3) равна 73. А площадь исходного квадрата 64. Так как 64 < 73, то, следовательно, все прямоугольники не могут быть различными. Поэтому найдутся два равных прямоугольника.
Приложение 3
В качестве апробации результатов исследования было составлено и проведено занятие математического кружка в 5 А классе МБОУ СОШ №11 с последующим анкетированием. Тема занятия «Принцип Дирихле. Решение задач» и состоит оно из трех этапов: теоретический, практический, рефлексия (анкетирование). На первом этапе познакомились с краткой биографией Дирихле ПетерГустава и с помощью формулировки Принципа Дирихле и методов сравнения, анализа и обобщения составлен алгоритм решения задач с помощью указанного принципа. Для второго этапа занятия было создано мультимедийное методическое пособие для первичного закрепления у обучающихся навыков решения подобных задач. Далее на этом этапе предлагались для решения задачи из приложения 2 к настоящей работе. Практические задачи были распределены по принципу: от простого к сложному. Перед учащимися одна за другой ставились посильные задачи, решение которых давало им новые сознательные знания. В качестве вспомогательного элемента использовалась презентация. Для осуществления этапа рефлексии составлена анкета, в которой содержатся вопросы закрытого и открытого типов.
Анкета
1.Решали ли вы логические задачи на уроках математики?
2.Встречали ли вы логические задачи на олимпиадах и конкурсах?
3.Понравилось ли вам занятие кружка сегодня ?
4. Узнали ли вы что-то новое для себя сегодня на занятии кружка? Если да, то напишите ,что………………………………………………………..
5.Читали ли вы о немецком математике Дирихле раньше?
6.Решали ли вы раньше задачи данного типа (если да, укажите метод, который чаще всего использовали)…………………………………………
7.Изменилось ли ваше представление о логических задачах после занятия кружка?
8.Будете ли вы использовать принцип Дирихле при решении конкурсных задач в дальнейшем?
9.Напишите хотя бы оно преимущество принципа Дирихле при решении логических задач……………………………………………
10.Перечислите недостатки принципа Дирихле при решении логических задач………………………………………………………………
Анализ результатов анкетирования. На занятии присутствовало 18 учащихся 5 класса повышенного уровня обучения. Получены следующие результаты анкетирования: на первый вопрос ответили -«да» 4 учащихся (%),на второй вопрос ответили - «да»18 учащихся (100%) ,на третий вопрос-«да»18 учащихся (100%),на четвертый вопрос ответили -«да»18 учащихся (100%) и написали ,что узнали новый метод решения олимпиадных задач. На пятый вопрос ответ был -«нет»у 100% учащихся.На шестой вопрос 70 % ответили ,что решали задачи данного типа способом перебора возможных вариантов. На седьмой и восьмой вопросы –ответы «да» у 100% учащихся. Преимуществами применения принципа Дирихле назвали:четкость представления, оригинальность, экономичность во времени.Недостатком была названа «боязнь» неверного определения «клеток » и «зайцев».
