Файл: 1. теоретические сведения дискретизация. Вводные замечания.docx

1.2. Наложение и спектры дискретных сигналов

Предположим, мы выполнили дискретизацию сигнала в определенной временной области с интервалом T (в секундах) (т.е. частота дискретизации равна 1/T (в герцах)). Видно (рис. 44), что в исходном сигнале есть еще одна частотная составляющая с таким же набором дискретных значений. Следовательно, этот частотный компонент можно ошибочно принять за компонент с более низкой частотой. Это и есть наложение. С точки зрения анализа следствий или поиска решения задачи наложения исследовать наложение лучше в частотных координатах.

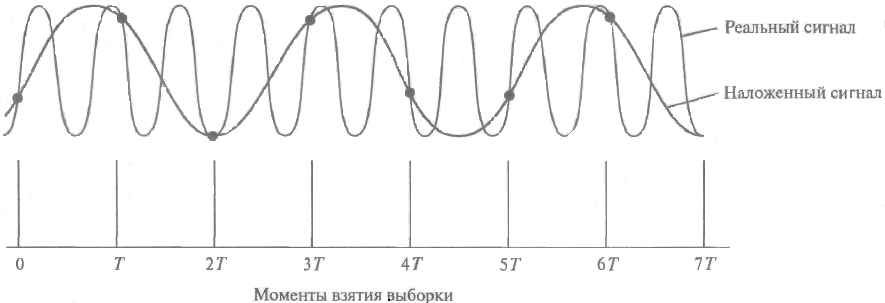
Рис. 44. Пример наложения во временных координатах. Обратите внимание на то, что оба сигнала имеют одинаковые значения в одних и тех же точках, хотя их частоты различны
На рис. 45 показан процесс дискретизации, который можно рассматривать как умножение аналогового сигнала x(t) на выборочную функцию p(t). Функция p(t) состоит из импульсов единичной амплитуды с шириной dt (бесконечно малой величиной) и периодом Т. Спектр сигнала x(t), функция p(t) и их произведение показаны на рис. 2.5. Заметим, что X'(f) – это свертка X(f) и P(f), следовательно, умножение во временных координатах эквивалентно свертке в частотных координатах.

Для дискретного сигнала (рис. 45, г) следует отметить такие моменты:

• 
  Спектр идентичен исходному аналоговому спектру, только повторяется в точках, кратных частоте дискретизации F_s. Компоненты более высокого порядка с центрами в точках, кратных F_s, называются зеркальными частотами.
  
• 
  Если частота дискретизации F_s недостаточно высока, то зеркальные частоты с центром в F_s будут, например, накладываться на частоты основной полосы. В этом случае полезную информацию, содержащуюся в сигнале, невозможно отличить от его образа в области наложения.
  
• 
  Перекрывание (или наложение) происходит в районе точки F_N, равной половине частоты дискретизации. Эту точку часто называют максимальной частотой сигнала, частотой Найквиста, частотой Котельникова и т.п.
  

На практике наложение существует всегда

---

, из-за шума и наличия энергии сигнала за пределами полосы частот, которая представляет интерес. Поэтому задача разработчика – определить уровень допустимого наложения, создать подходящий фильтр защиты от наложения спектров и выбрать подходящую для этого частоту дискретизации.


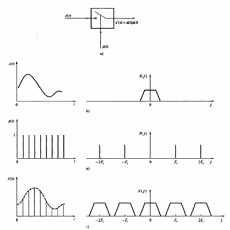
Рис. 45. Описание процесса дискретизации во временной и частотной областях. Сравните спектры сигнала

до (б) и после (г) дискретизации. Обратите внимание на изменения в дискретном сигнале и, в частности,

на то, что спектр дискретного сигнала повторяется в точках, кратных частоте дискретизации Fs

1.3 Демонстрация наложения с помощью Simulink

Сейчас мы посмотрим, как влияет недостаточная частота дискретизации. Для этого воспользуемся слегка модернизированным примером из справки MATLAB, показанном на рис. 46.

Пример 2. Составить схему системы осуществляющей анализ спектра двух синусоид. Исходные данные:

Амплитуда: 1В;

Частота: 15 Гц, 40Гц;

Фаза: 0 град;

Период дискретизации: 0.001 с;

Отсчетов на кадр: 128.


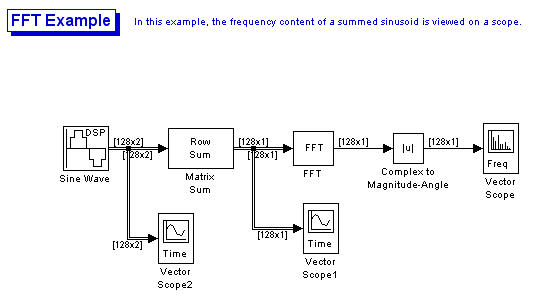
Рис. 46. Модернизированный пример применения

быстрого преобразования Фурье FFT в Simulink
От стандартного примера данный пример отличается только двумя блоками: Vector Scope1 и Vector Scope2. Vector Scope1 показывает итоговый сигнал, Vector Scope2 показывает каждую синусоиду отдельно.

Настройка параметров блоков.

1. Двойной клик мышью на блоке Sine Wave block: откроются параметры блока. Установите там следующие значения:

Amplitude = 1

Frequency = [15 40]

Phase offset = 0

Sample time = 0.001

Samples per frame = 128

Согласно этим данным, блок Sine Wave выведет две синусоиды с одинаковыми амплитудами, фазами и интервалами дискретизации. Частота одной синусоиды 15 Гц, другой – 40 Гц. В данном случае алгоритм нашей модели ориентирован на обработку последовательности кадров (векторов) сигнала (Frame Based). Векторная или кадровая форма реализации алгоритма обработки в модели, как правило, позволяет значительно ускорить процесс моделирования в нереальном времени. В этой форме для формирования кадров из непрерывно потока отсчетов используется буферная память.

---

Сохраним изменения и закроем окно.

2. Блок Matrix Sum. В окне параметров задайте следующее значение:

Sum along = Rows

3. Так как каждый отдельный сигнал это отдельный столбец матрицы, нам нужно сложить значения синусоид на каждом временном шаге, чтобы получить итоговый сигнал. Для этого в блоке Complex to Magnitude-Angle установим:

Output=Magnitude

Этот блок конвертирует комплексные значения FFT и рассчитывает амплитуду.

4. Блок Vector Scope:

Закладка Scope Properties

Input domain = Frequency

Закладка Axis Properties

Frequency units = Hertz

Frequency range = [0...Fs/2]

Отмечаем (галочкой) пункт «Inherit sample time from input»

Amplitude scaling = Magnitude

6. Блоки Vector Scope1 и Vector Scope2 оставляем без изменений.

7. Запустите модель. Vector Scope показывает два пика на 0.015 и 0.04 кГц, как и следовало ожидать (рис.47):

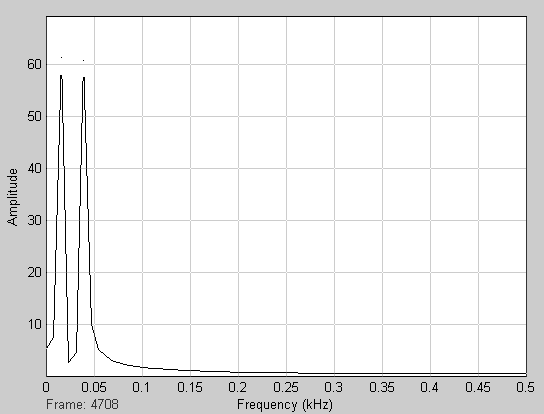
Рис. 47. График спектра двух синусоид
Теперь изменим частоту дискретизации в блоке Sine Wave так, чтобы она не соответствовала условиям теоремы Котельникова. Например, поставим Sample Time = 1/60. После этого на графике мы увидим новую частоту, которой не было в исходном сигнале (рис.48). Это и есть наложение (aliasing).


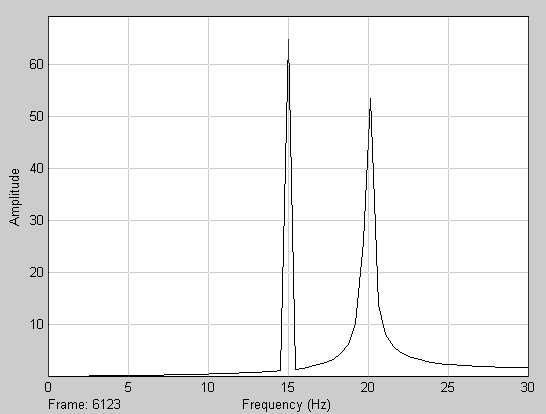
Рис. 48. Наложение
Синусоиды с частотой 40 Гц на этом графике вообще не видно. Это произошло из-за того, что мы указали в настройках Vector Scope отображать график в интервале [0...Fs/2]. Измените его на [0...Fs].

2. ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ

1. Ознакомьтесь с п.1. Выполните все приведенные примеры.

2. Создайте из блоков Simulink простую модель аналого-цифрового преобразователя. Используйте в качестве дискретизатора блок Zero-Order Hold, в качестве квантователя – Qantizer. Выведите графики исходного, дискретизированного и цифрового сигналов. Объясните роль каждого блока.

3. В примере на рис. 46 замените блоки FFT, Complex to Magnitude-Angle и Vector Scope на один блок Spectrum Scope.

4. В примере на рис. 46 настройте блок Sine Wave так, чтобы он генерировал 4 синусоиды с разными частотами.

5. Поменяйте частоту дискретизации в задании 3. Покажите, как происходит наложение.

---

Требования к содержанию отчета: составьте отчет в электронном виде, включающий все команды, вводимые в командной строке MATLAB и все полученные графики.

3. КОНТРОЛЬНЫЕ ВОПРОСЫ

1. С какой частотой необходимо дискретизировать аналоговый сигнал, чтобы его можно было восстановить без потерь?

2. В чем различие спектров аналогового и дискретизированного сигналов?

3. Объясните причину появления эффекта наложения.

4. Литература

1. Айфичер Э.С., Джервис Б.У. Цифровая обработка сигналов: практический подход [Текст]: Пер с анг. – М.: Издательский дом «Вильямс», 2004. – 992с.

2. Дьяконов В.П. MATLAB 6.5 SP1/7 + Simulink 5/6. Обработка сигналов и проектирование фильтров [Текст] – М.: СОЛОН-Пресс, 2005. – 576 с.

---