Один з найбільш швидких алгоритмів, відомих у цей час, алгоритм NFS (Number Field Sieve) може виконати факторизацію великого числа N (із числом десяткових розрядів більше 120) за число кроків, оцінюваних величиною

У 1994 р. було факторизовано число з 129 десятковими цифрами. Це вдалося здійснити математикам А.Ленстра й М.Манассі за допомогою організації розподілених обчислень на 1600 комп’ютерах, об’єднаних мережею, протягом восьми місяців. На думку А.Ленстра та М.Манассі, їхня робота компрометує криптосистеми RSA і створює більшу погрозу їхнім подальшим застосуванням. Тепер розроблювачам криптоалгоритмів з відкритим ключем на базі RSA доводиться уникати застосування чисел довжиною менше 200 десяткових розрядів. Останні публікації пропонують застосовувати для цього числа довжиною не менше 300 десяткових розрядів.

4 Схема шифрування Поліга - Хеллмана

Схема шифрування Поліга - Хеллмана подібна RSA. Розглянута схема не є симетричним алгоритмом, оскільки використовуються різні ключі для шифрування та розшифрування. З іншого боку її не можна віднести й до класу криптосистем з відкритим ключем, тому що ключі шифрування та розшифрування легко виходять один з одного. Обидва ключі (відкритий і таємний) необхідно тримати в таємниці.

Аналогічно схемі RSA криптограма C і відкритий текст M визначаються зі співвідношень:

_, (4.14)

_, (4.15)

де

. (4.16)

На відміну від алгоритму RSA у цій схемі число N не визначається через два великих простих числа; число N повинне залишатися частиною таємного ключа. Якщо хто-небудь довідається значення та N, він зможе обчислити значення .

Не знаючи значень або , зловмисник буде змушений обчислювати значення

.

---

Відомо, що це є важкою задачею. Схема шифрування Поліга - Хеллмана запатентована в США [9] і Канаді.

5 Алгоритм шифрування Ель Гамаля

Алгоритм Ель Гамаля, розроблено в 1985 р., може бути використаний як для шифрування, так і для цифрових підписів. Безпека схеми Ель Гамаля обумовлена складністю обчислення дискретних логарифмів у кінцевому полі.

Для того щоб генерувати пари ключів (відкритий ключ і таємний ключ ), спочатку вибирають деяке велике просте число P і велике ціле число G степені якого за модулем P породжують велику кількість елементів множини , причому . Числа P й G можуть бути поширені серед групи користувачів.

Потім вибирають випадкове ціле число , причому . Число є таємним ключем і повинне зберігатися в секреті.

Далі обчислюють відкритий ключ

. (4.17)

Для того, щоб зашифрувати повідомлення М, вибирають випадкове ціле число , що задовольняє такі умови:

, (4.18)

. (4.19)

Потім обчислюють числа

(4.20)

(4.21)

Пари чисел (а,b) є шифротекстом. Помітимо, що довжина шифротексту вдвічі більша довжини вихідного відкритого тексту М.

Для того щоб розшифрувати шифротекст (а,b), обчислюють

. (4.22)

Довести, що співвідношення (4.22) справедливо, можна виходячи з (3.17) , (3.20) і (3.21), оскільки

---

.

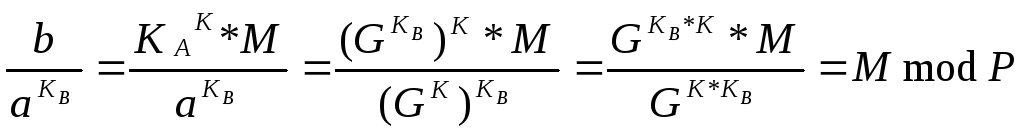Наприклад, виберемо Р = 17, G = 5, таємний ключ = 2. Обчислюємо

.

Отже, відкритий ключ = 8.

Нехай повідомлення М = {Д}={5}.

Виберемо деяке випадкове число K = 3. Перевіримо умову (3.19) дійсно НСД (3,16) =1. Обчислюємо пари чисел а та b:

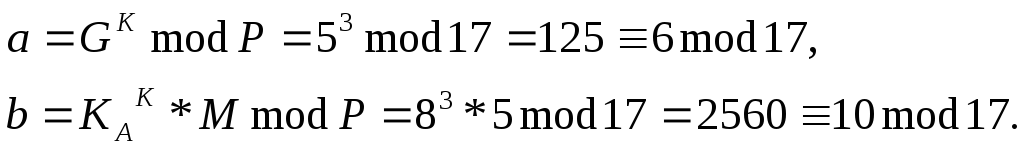
Таким чином, шифротекстом для літери Д є пара чисел (6,10).

Виконаємо розшифрування цього шифротексту. Обчислюємо повідомлення М, використовуючи таємний ключ

.

Вираз

можна подати у вигляді

.

Розв’язуючи дане порівняння, знаходимо М = 5.

У реальних схемах шифрування необхідно використовувати як модуль P велике ціле просте число, що має у двійковому поданні довжину від 512 до 1024 бітів.

У системі Ель Гамаля відкритого шифрування той самий ступінь захисту, що для алгоритму RSA з модулем N з 200 знаків, досягається вже при модулі P в 150 знаків. Це дозволяє в 5-7 разів збільшити швидкість обробки інформації. Але у такому варіанті відкритого шифрування немає підтвердження достеменності повідомлень.

Система Ель Гамаля не позбавлена певних недоліків. Серед них можна зазначити такі:

1 Відсутність семантичної стійкості. Якщо G – примітивний елемент множини , то за поліноміальний час можна визначити чи є деяке число x квадратичним відрахуванням. Це робиться піднесенням числа x у степінь за модулем P

.

Якщо результат дорівнює 1, то х – квадратичне відрахування за модулем Р, якщо –1 , то х – квадратичне невирахування. Далі пасивний зловмисник перевіряє, чи є G^K і квадратичними відрахуваннями. буде квадратичним відрахуванням тоді й тільки тоді, коли і G^K , і будуть квадратичними відрахуваннями. Якщо це так, то буде квадратичним відрахуванням тоді й тільки тоді, коли саме повідомлення М буде квадратичним відрахуванням. Тобто пасивний зловмисник одержує деяку інформацію про вихідний текст, маючи лише шифрований текст і відкритий ключ одержувача.

---

2 Подільність шифру. Якщо дано шифрований текст (a, b), можна одержати інший шифрований текст, змінивши тільки другу частину повідомлення. Справді, помноживши b на G^U (U0), можна одержати шифротекст для іншого вихідного повідомлення .

6 Схема шифрування Рабіна

Схема Рабіна була розроблена в 1979 році й може застосовуватися тільки для шифрування даних. Безпека алгоритму спирається на складність пошуку коренів за модулем складеного числа.

Для генерації ключів вибирається пара простих чисел , таких що

(4.23)

Ці прості числа і є таємним ключем. Відкритим ключем є число

. (4.24)

Для шифрування повідомлення , де , обчислюється

. (4.25)

Для розшифрування повідомлення за допомогою китайської теореми про залишки обчислюється:

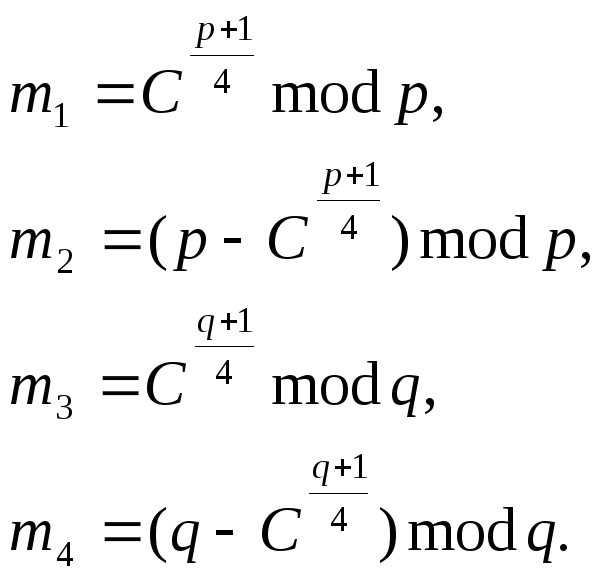(4.26)

Потім вибираються два цілих числа

(4.27)

Чотирма можливими рішеннями є:

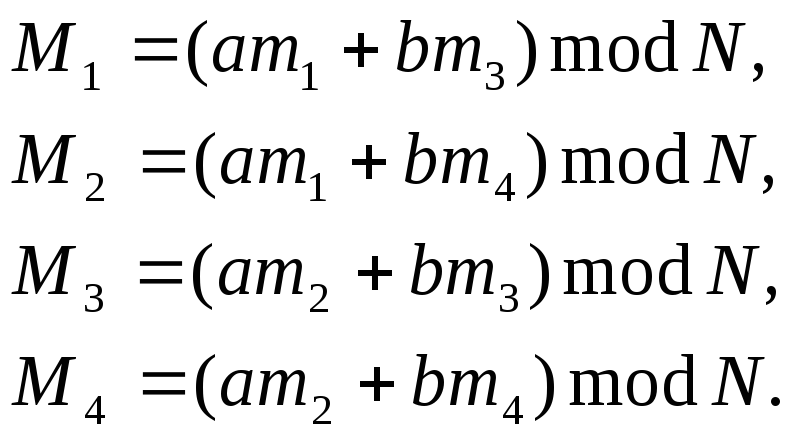(4.28)

Одне із чотирьох результатів, і , є повідомлення .

Наприклад, виконаємо шифрування тексту , використовуючи схему шифрування Рабіна. Згідно з (4.23) виберемо пари чисел , нехай й . Тоді, відкритий ключ N=77.

Шифротекст C згідно з (4.25)

.

---

Виконаємо розшифрування. Виходячи з (4.26), маємо

Згідно з (4.27)

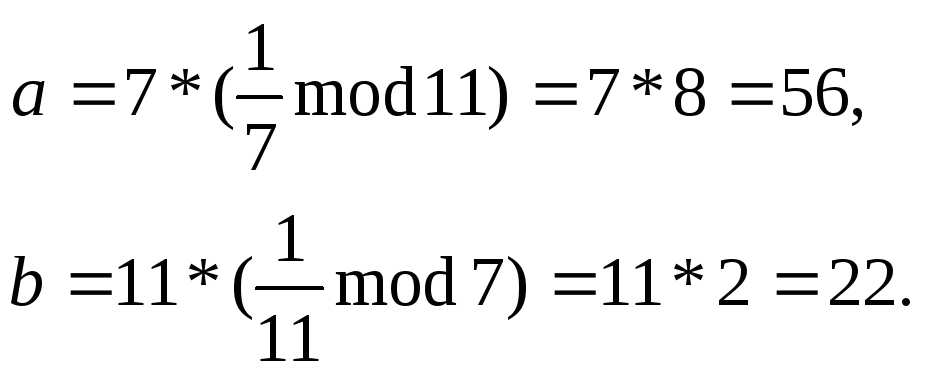
Тоді за (4.28) одержимо

Дійсно, одне із чотирьох значень, а саме: і є відкритий текст .

Задачі

1. Використовуючи криптосистему RSA, виконати цифровий підпис для повідомлення М={2, 3, 4}. Відомо, що P=37, Q=17. Відповідь надати у вигляді послідовного набору чисел.

2. Виконайте алгоритм RSA для таких значень параметрів P, Q, 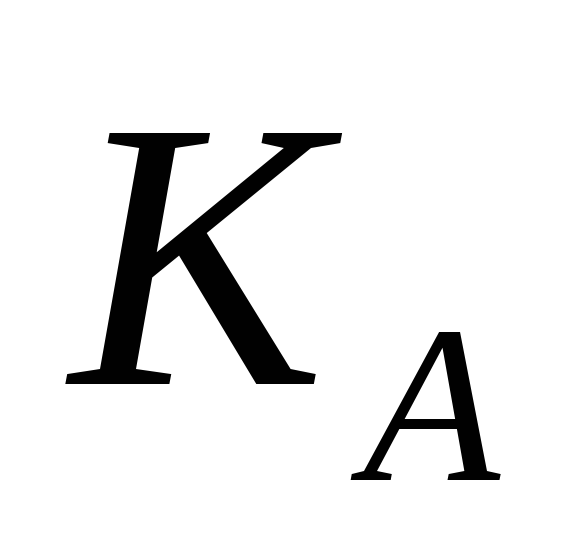, , 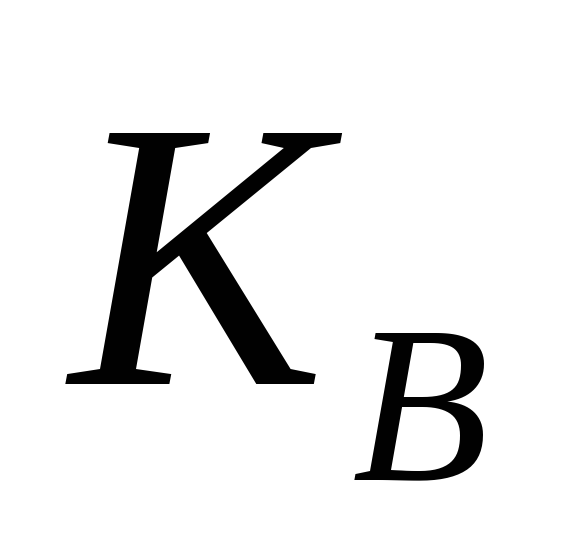M:

P=7, Q=13, =5, M=5;

P=5, Q=11, = 9, M =8;

P=13, Q=11, =17, M=9;

P=17, Q=7, =11, M =7.

3. Відомо, що в системі RSA відкритим ключем деякого користувача є 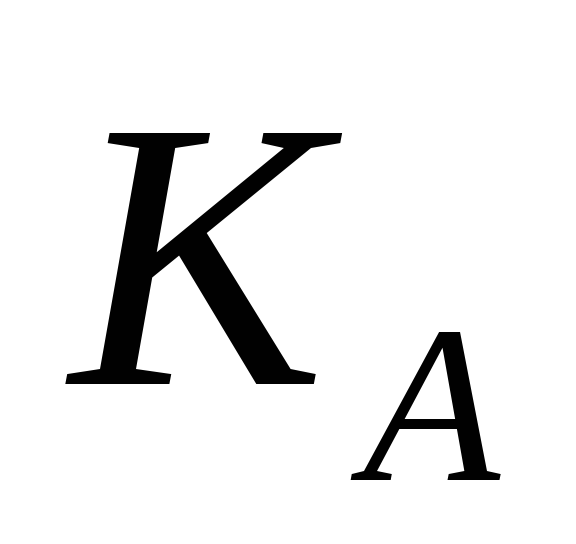=5, n=576. Встановити таємний ключ .

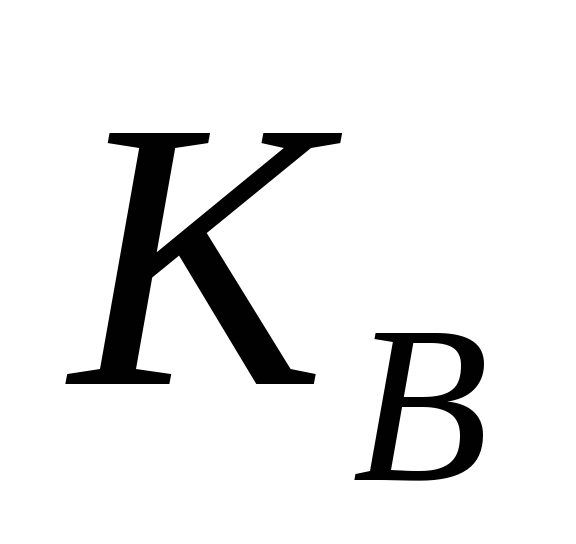4. У криптосистемі з відкритим ключем, використовує RSA, було перехоплено шифрований текст C=16, був зашифрований відкритим ключем 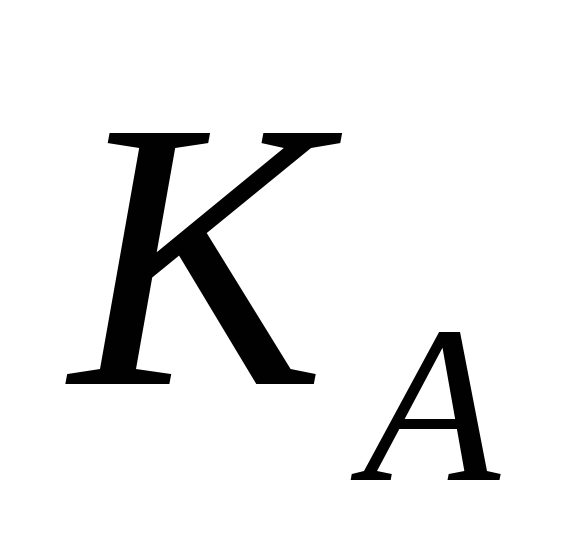=7, N=21. Встановити відкритий текст M.

5. Нехай в деякій системі RSA кожен з користувачів має особистий таємний ключ 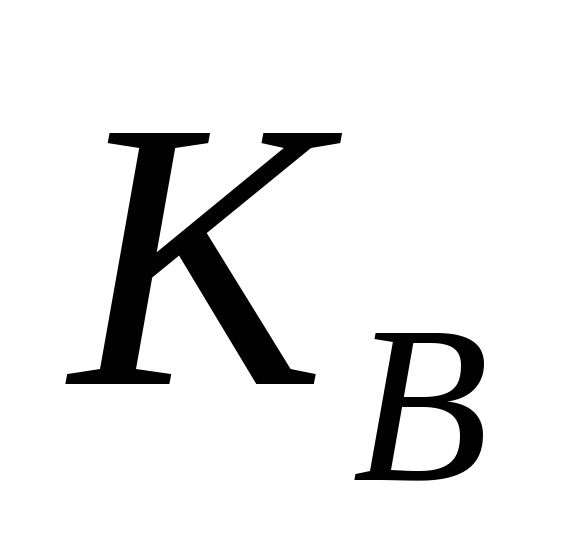та відкритий ключ 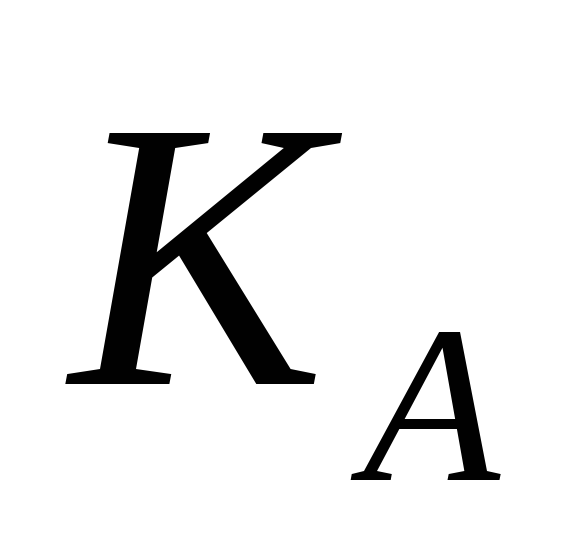. Припустимо, що деякий користувач довідався, що секрет його таємного ключа розкрито. Але замість генерації нового модуля порівняння, він вирішує генерувати нові таємний та відкритий ключі. Наскільки це безпечно?

6. У криптосистемі Ель Гамаля виконати шифрування відкритого тексту М={2, 3, 4} (зашифрування та розшифрування). Обрати числа P та Q із запропонованого набору чисел {15, 17, 20, 28, 24, 21}. Таємний ключ Х та число К обрати згідно з вимогами шифру.

7. Виконайте алгоритм Ель Гамаля для таких значень параметрів P, G, X, K, M, a, b:

---

Смотрите также файлы

• Лекция 7.doc

• Лекция 8.doc

• Лекция 9.doc

• Лекция 10.doc

• Лекция 11.doc