1. Решить систему методом Крамера и методом Гаусса.







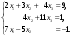
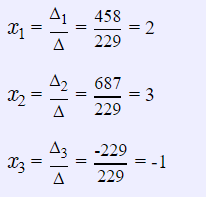
2. Установить совместность системы и найти общее решение.



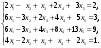
Выпишем расширенную и основную матрицы:

2	-1	1	2	3	2
6	-3	2	4	5	3
6	-3	4	8	13	9
4	-2	1	1	2	1
x1	x2	x3	x4	x5

Умножим 1-ую строку на (-3). Добавим 2-ую строку к 1-ой:

0	-1	-2	-4	-3	0
-3	2	4	5	3	-6
-3	4	8	13	9	-6
-2	1	1	2	1	-4

---

Умножим 2-ую строку на (-1). Добавим 3-ую строку к 2-ой:

0	-1	-2	-4	-3	0
0	2	4	8	6	0
-3	4	8	13	9	-6
-2	1	1	2	1	-4

В матрице B 1-ая и 2-ая строки пропорциональны, следовательно, одну из них, например 1-ю, можно вычеркнуть. Это равносильно вычеркиванию 1-го уравнения системы, так как оно является следствием 2-го.

0	2	4	8	6	0
-3	4	8	13	9	-6
-2	1	1	2	1	-4

Умножим 2-ую строку на (-2). Умножим 3-ую строку на (3). Добавим 3-ую строку к 2-ой:

0	2	4	8	6	0
0	-5	-13	-20	-15	0
-2	1	1	2	1	-4

---

Умножим 1-ую строку на (5). Умножим 2-ую строку на (2). Добавим 2-ую строку к 1-ой:

0	0	-6	0	0	0
0	-5	-13	-20	-15	0
-2	1	1	2	1	-4

Определим ранг основной системы системы.

0	0	-6	0
0	-5	-13	-20
-2	1	1	2

Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля. Ранг этой системы равен rangA=3.
Определим ранг расширенной системы системы.

0	0	-6	0	0	0
0	-5	-13	-20	-15	0
-2	1	1	2	1	-4

Ранг этой системы равен rangB=3.
rang(A) = rang(B) = 3. Поскольку ранг основной матрицы равен рангу расширенной, то система является совместной.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x₁,x₂,x₃, значит, неизвестные x₁

---

,x₂,x₃ – зависимые (базисные), а x₄,x₅ – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.
Определим ранг расширенной системы системы.

0	0	0	0	6	0
0	-5	-15	0	13	20
-2	1	1	-4	-1	-2
x2	x3

Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
= 6x₄
- 5x₂ - 15x₃ = 13x₄ + 20x₅
- 2x₁ + x₂ + x₃ = - 4x₁ - x₄ - 2x₅
Получили соотношения, выражающие зависимые переменные x₁,x₂,x₃ через свободные x₄,x₅, то есть нашли общее решение:
x₃ = 6x₄
x₂ = - ¹³/₅x₄ - 4x₅
x₁ = 2x₁ - ⁴/₅x₄ - x₅
Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Система является неопределенной, т.к. имеет более одного решения.

3.Даны координаты вершин треугольника АВС. Найти: 1) уравнения сторон треугольника, представленные в общем виде и с угловым коэффициентом; 2) величину внутреннего угла А, выраженное в градусах; 3) уравнение высоты СН, ее длину; 4) уравнение медианы АМ, ее длину и координаты точки К пересечения этой медианы с высотой СН.

---

А (–8; –3), В (4; –12), С (8; 10).

Даны координаты вершин треугольника: A(-8,-3), B(4,-12), C(8,10).
Длина сторон треугольника.
Расстояние d между точками M₁(x₁; y₁) и M₂(x₂; y₂) определяется по формуле:




Уравнение прямой
Прямая, проходящая через точки A₁(x₁; y₁) и A₂(x₂; y₂), представляется уравнениями:

Уравнение прямой AB
Каноническое уравнение прямой:

или

или
y = ^-3/₄x -9 или 4y + 3x +36 = 0
Уравнение прямой AC
Каноническое уравнение прямой:

или

или
y = ¹³/₁₆x + ⁷/₂ или 16y -13x - 56 = 0
Уравнение прямой BC
Каноническое уравнение прямой:

или

или
y = ¹¹/₂x -34 или 2y -11x +68 = 0
Площадь треугольника
Пусть точки A₁(x₁; y₁), A₂

---

Смотрите также файлы

• Программа курса внеурочной деятельности по интеллектуальнопознавательному направлению для обучающихся с легкой умственной отсталостью.docx

• Обязательства в гражданском праве понятие и классификация.docx

• Руководство студентки 2 а группы специальности 44. 02. 02 Преподавание в начальных классах.docx

• Сыроежки.docx

• Туелсіздікаманаты бабамны поэзиялы.docx