Файл: Цифровая безопасность. Шифрование данных.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 17.10.2024

Просмотров: 5

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Лабораторная работа № 8
Тема: Цифровая безопасность. Шифрование данных.
Цель работы: Освоить технологию обеспечения безопасности ОС Windows 10 и методы криптографической защиты информации.
Краткие сведения из теории
Цифровая безопасность – это комплекс мер, направленных на защиту конфиденциальности, целостности и доступности информации от вирусных атак и несанкционированного вмешательства.

Основные меры, связанные с цифровой безопасностью, заключаются в следующем:

  • Установка лицензионных операционных систем и программного обеспечения. Нелицензионнaя ОС может содержать вредоносные закладки, а также не позволяет делать обновление. Если вы не хотите покупать OS, можно воспользоваться бесплатными аналогами на базе Linux: Ubuntu, Linux Mint, Fedora.

  • Регулярное обновление операционной системы. Обновления зачастую содержат исправление брешей в безопасности.

  • Установка антивируса для пользователей Windows. Антивирус снизит риск заражения компьютера широко распространенными вредоносными программами. Пользователям MacOS или Linux антивирус не требуется.

  • Синхронизация локальных папок с Облаком. Если есть оперативный бэкап, то в случае необходимости можно сразу продолжить работу без необходимости полного восстановления из бэкапа.

  • Создание резервной копии диска.


К методам обеспечения безопасности на ПК относят:

  • использование атрибутов файлов и каталогов типа «скрытый», «только для чтения»;

  • сохранение важных данных на внешних магнитных дисках или флешках;

  • помещение данных в защищенные паролем архивные файлы;

  • регулярная проверка компьютерной системы на вирусы.


Windows 10 содержит полноценную и надежную встроенную систему безопасности, которая работает непрерывно, включая антивирусную программу «Защитник Windows», брандмауэр и другие функции. Благодаря обновлениям вы всегда будете получать новейшие функции защиты, и доплачивать за это не придется.

Антивирусная программа «Защитник Windows» обеспечивает комплексную постоянную защиту в реальном времени от угроз со стороны ПО, такого как вирусы и вредоносные программы, в электронной почте, приложениях и в Интернете.


Шифрование данных
Для защиты информации от несанкционированного доступа применяют различные методы шифрования информации. Составными частями современных алгоритмов шифрования являются шифры замены, перестановки и Вернама. Шифр замены является простейшим. Он осуществляет преобра­зование путем замены символов открытого текста в зашифрованный.

Пусть X и Y - два алфавита открытого и, соот­ветственно, шифрованного текста, состоящие из оди­наковых символов. Пусть g(х) отображение X в Y. Это означает, что каждой букве x алфавита X, однозначно соответствует оп­ределенная буква y алфавита Y. Причем разным буквам алфавита Х соответствуют разные буквы алфавита Y.

Покажем использование шифра замены на при­мере шифрования слова "АСТАНА".

Алфавит исходный:

АБВГДЕЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ

Алфавит замены:

ЯЮЭЬЫЪЩШЧЦХФУТСРПОНМЛКЙИЗЖЕДГВБА

Открытый текст "АСТАНА", зашифрованный текст "ЯОНЯТЯ".

Расшифровывание происходит в обратном порядке.
Шифр перестановки заключается в перестанов­ке букв открытого текста в закрытый текст по опре­деленному закону. Про­стейшим видом шифра пе­рестановки является разбивка открытого текста на отдельные группы символов, которые затем меняются местами по заданному закону.

Например, открытый текст КРАСНАЯ ПЛО­ЩАДЬ-ЦЕНТР ГОРОДА МОСКВЫ разбивается на группы, содержащие пять символов: КРАСН-АЯ ПЛ - ОЩАДЬ - -ЦЕНТ - Р ГОР - ОДА М - ОСКВЫ - ко­торые затем переставляются по закону: ключ: - (1 - 3; 2 - 4; 3 - 2; 4 - 5; 5 - 1) В результате перестановки зашифрованный текст будет иметь вид: АСРНК ПЯЛААДЩЬОЕНЦТ ГО РРАДМАКВСЫО.

Расшифровывание происходит в обратном порядке. Следует отметить, что отдельно взятые шифры перестановки и замены не обладают криптографи­ческой стойкостью, т.е. легко расшифровываются. Однако их совместное сочетание позволяет полу­чить значительно более стойкие шифры.

Табличные шифры появились в конце XIV столетия. Они относятся к шифрам перестановки и являются блочными шифрами, где длина блока определяется размером таблицы. Одним из самых простых табличных шифров является перестановка, для которой ключом служит размер таблицы. Например, сообщение записывается в таблицу поочередно по столбцам. После заполнения таблицы текстом сообщения по столб­цам для формирования зашифрованного текста считывают содержимое таблицы по строкам. При дешифровании дейст­вия выполняют в обратном порядке. Естественно, отправитель и получатель сообщения долж­ны заранее условиться об общем ключе в виде размера таблицы.


Рассмотрим шифрование сообщения «Прилетаю седьмого в полдень». В качестве ключа примем размер таблицы 4x6 (4 строки, 6 столбцов). Сообщение записывается в таблицу по столбцам (таблица 1). Пробелы при этом могут игнорироваться.
Таблица 1 – Шифрование методом простой табличной перестановки.

П
Е
С
М
В
Д

Р
Т
Е
О
П
Е

И
А
Д
Г
О
Н

Л
Ю
Ь
О
Л
Ь

 

Для формирования шифротекста содержимое таблицы считывают по строкам. Таким образом, результатом шифрования рассматриваемого сообщения будет текст:

ПЕСМВДРТЕОПЕИАДГОНЛЬЮОЛЬ

Несколько большей стойкостью к раскрытию обладает метод шифрования, называемый одиночной перестановкой по ключу. Этот метод отличается от предыдущего тем, что столбцы переставляются по ключевому слову, фразе или набору чисел длиной в строку таблицы.

Применим в качестве ключа шифрования сообщения из предыдущего примера слово КОРОВА. Строится таблица с количеством столбцов, равным количеству букв в ключевом слове. Ключ шифрования записывается в первую строку таблицы. Затем во второй строке таблицы для каждой буквы записывается ее номер в слове согласно следованию букв в алфавите. Если буквы повторяются - они нумеруются слева направо. Далее таблица заполняется шифруемым сообщением по столбцам аналогично предыдущему рассматриваемому методу (таблица 2).
Таблица 2 – Шифрование одиночной перестановкой по ключу.

К
О
Р
О
В
А



















П
Е
С
М
В
Д

Р
Т
Е
О
П
Е

И
А
Д
Г
О
Н

Л
Ю
Ь
О
Л
Ь


Следующим шагом шифрования является перестановка столбцов в соответствии с упорядоченными номерами букв ключа. Результат перестановки представлен в таблице 3.
Таблица 3 – Шифрование одиночной перестановкой по ключу.

А
В
К
О
О
Р



















Д
В
П
Е
М
С

Е
П
Р
Т
О
Е

Н
О
И
А
Г
Д

Ь
Л
Л
Ю
О
Ь


При считывании содержимого таблицы 3 по строкам получим следующий шифротекст:
ДВПЕМСЕПРТОЕНОИАГДЬЛЛЮОЬ

 

Квадрат Полибия
Квадрат Полибия относится к шифрам простой табличной замены, в которых буквы исходного текста заменяются по определенному правилу другими буквами того же алфавита. За два века до нашей эры греческий полководец и историк Полибий изобрел для целей шифрования квадратную таблицу размером 5х5, заполненную буквами алфавита в случайном порядке.

Рассмотрим прямоугольник, часто называемый доской Полибия (таблица 4). В такой прямоугольник записываются буквы алфавита, причем схема записи (расположение букв в таблице) держится в тайне и составляет ключ шифрования.

Таблица 4 – Пример квадрата Полибия.

 
А
Б
В
Г
Д
Е

А
А
Б
В
Г
Д
Е

Б
Ж
З
И
К
Л
М

В
Н
О
П
Р
С
Т

Г
У
Ф
Х
Ц
Ч
Ш

Д
Щ
Ъ
Ы
Ь
Э
Ю

Е
Я


.
Й
-
Ё


В алфавит могут включаться символ пробела, знаки препинания или редко используемые символы (такие как ё, й). В процессе шифрования каждая буква открытого текста представляется в шифротексте парой букв, указывающих строку и столбец, в которых расположена данная буква. Так представлениями букв В, Г, П, У будут АВ, АГ, ВВ, ГА соответственно.

Если использовать приведенный выше квадрат в качестве ключа шифрования, то фраза «ПРИМЕР ШИФРОВАНИЯ» будет зашифрована в набор символов:
«ВВВГБВБЕАЕВГЕБГЕБВГБВГВБАВААВАБВЕА».
В приведенном примере размер шифротекста превышает размер исходного текста в 2 раза. При компьютерной реализации номера строк и столбцов таблицы можно задавать в виде цифр. Тогда, учитывая, что получившийся квадрат имеет по 6 строк и 6 столбцов, для кодирования каждой буквы будет достаточно 8 бит (4 бита для номера строки, 4 бита для номера столбца). В итоге один символ зашифрованного текста будет иметь длину 1 байт.
Шифр Вернама
Широко применяется для шифрования двоичных кодов шифр Вернама. В этом шифре шифрование сводится к поразрядной операции сложения по модулю 2 фрагментов исходного сообщения с двоичным ключом. Для шифрования исходное сообщение делится на фрагменты равные длине ключа.

В = А  К,

где К - ключ

А - фрагмент исходного сообщения,

В - результат шифрования.

Рассмотрим пример.

А = 1011000101110101



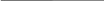К = 1101101001000011
В = 0110101100110110

На приемной стороне выполняются аналогичные действия над принятым зашифрованным кодом В и ключом К.
В = 0110101100110110



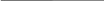К = 1101101001000011
А = 1011000101110101
Ключ К - случайный код. Для обеспечения высокой стойкости шифра к взлому требуется периодически менять ключ К. Кроме того, чем больше длина ключа, тем труднее расшифровать текст.
Порядок выполнения лабораторной работы


  1. Изучить теоретический материал.

  2. Выполнить задания.

  3. Ответить на контрольные вопросы.


Задание 1

- Пароль (пин-код) банковской карточки содержит 4 цифры, каждый из 0,1,2,...,9 возможных значений. Злоумышленнику удалось подглядеть только последнюю цифру. Какова вероятность

Смотрите также файлы