Файл: Наибольших успехов в этом достигли технические науки и производственные процессы механика и машиностроение, электротехника, строительное дело, транспорт и ряд других.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.10.2024
Просмотров: 17
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3. Движения систем
Преобразования системы
В соответствии с положениями диалектики развития материального общества, под движением принимается все происходящие в природе и обществе процессы.
Следовательно, можно говорить о химическом движении (синтезе и разложении химических соединений), органическом движении (жизненных процессов растений и животных), движение экономических систем и т.п.
Движение любой системы представляет некоторую последовательность изменение его состояния. Характеризуется состояние системы в некоторый времени U, вектором Zj, а состояние его в последующий момент времени Ti+1 вектором Zi и можно считать что произошел переход вектора Zj в вектор Zi+1 .
Правило, согласно которому каждому элементу этого множества ставится в соответствие элемент другого множества называется оператором. Говоря о переходе в систему новое состояние, оператором будем называть правило в соответствие, с которым происходит этот переход. Значение переменной или величина, над которой совершается операция, вызывающая переход в новое состояние, называется операндом.
Новое значение переменной, то есть новое состояние, возникшая под действием оператора на операнд, носит название образа.
Под воздействия некоторого оператора происходит переходы для некоторого множества операндом. Множество переходов для множества операндов будет называться преобразованием.
Любую систему, в которой происходят те или иные изменения (преобразования), в результате которых множества реакций системы некоторым образом зависит от множества входящих воздействий, можно рассматривать как преобразователь реализующей некоторую заданную зависимость Y=f(x), где Y – множество реакций системы, а х – множество входящих воздействий.
Поведение динамических систем
Все динамические системы можно разделить на 2 типа. В системах первого типа, более простых, между вектором входящих величин х и вектором исходящих величин у, существует однозначная функциональная зависимость. Следовательно, задания вектора входных величин полностью определяет вектор выходных величин.
В системах 2ого типа, более сложных, которые можно отнести большинство современных технических систем и практически все биологические и экономические системы, имеет место 2 ступени функциональных связей (зависимости). Одна из них описывает зависимость внутреннего состояния системы от вектора входящих величин, другая - зависимость вектора выходных величин от множества внутренних параметров системы и векторы выходных величин. Таким образом, при исследования систем 2ого типа рассматривается более сложная зависимость: Y(t)=F[X(t), Z(t)], где х – входные величины, а Z – внутреннее состояние системы.
Подавляющая большинство экономических систем представляет объекты, которые описываются системой дифференциальных уравнений. В системе дифференциальных уравнений описывается: движения небесных тел, ракет и спутников, электрические колебания и т.п.
Таким же уравнением описывается различные технические объекты управления и их регуляторы (механические, электромеханические и электронные). Системой дифференциальных уравнений может успешно применятся для описания рядов процессов в экономике. В частности, при изучении глобальных проблем динамики развития социально-экономических систем, для построения макроэкономических моделей экономики страны, рассматриваемой как одно целое.
Важнейшим вопросом анализа динамической системы является определение её динамических свойств, в частности характера переходного процесса, точности и устойчивости.
Каждая динамическая система может находит в одном из 3ьох состояний:
1) равновесном
2) переходном
3) периодическом
В равновесном состоянии системы называют такое её состояние, при котором сумма действующих на систему сил и моментов = 0. Состояние равновесия системы в пространстве выражается некоторой фиксированной точкой. При этом следует различать 2 вида равновесного состояния:
- статическое равновесие
- динамическое равновесие.
В качестве примера состояния статического равновесия можно привести состояние покоящегося физического тела, состоянии запасов некоторых объектов хранения на складе в течении тех периодов, когда они не расходуются и не пополняются и т.д.
Динамическое равновесие системы обуславливается действием на нее факторов, вызывающие в среднем равные и противоположны следствия, при чем мгновенное состояние системы могут отличаться от её среднего состояния в ту или другую сторону. Примерами является: сохранения неизменного среднего уровня воды в водохранилище гидроэлектростанции, при равных расходе и притоке ее; поддержанием неизменной в среднем температуры тела у здорового человека благодаря сложным автоматическим организмом терморегуляции.
В устойчивых системах автоматического регулирования, состояние динамического равновесия того или иного параметра обеспечивается за счет управляющих воздействий, вырабатываемых исполнительными устройствами системы и компенсирующие эффекты возмущающих воздействий.
Под переходным процессом понимается процесс изменение во времени координат (параметров системы), имеющих место при переходе ее из одного равновесного состояние в другое или из одного установившегося режима работы в другой. Переходный процесс в динамических системах возникают в результате воздействий, которые изменяет состояние структуру и параметры системы. Теоретически переходный процесс в линейной непрерывной системы длится бесконечно долго, поэтому из практических соображений вводится некоторая условная граница, окончание переходного процесса после которой величина, определяющая состояние системы, отличается от установившихся не более чем на выбранную некоторую малую величину.
Например, процесс остывание = Ti, в среде более низкой температуры -
, пока разность 
велика, то остывание происходит медленно. Однако по мере уменьшения 
скорость охлаждения тела увеличивается и температура тела Т приближается к температуре окружающей среды, хотя теоретически никогда ей не достигнет. Тем не менее, практически мы можем считать, что переходный процесс заканчивается в некоторый момент времени, начиная с которого 
, где 
- выбранная величина. Рассматриваемый пример типичен для, так называемых, апериодических, у которых при отклонения системы от состояния равновесия координаты, описывающее её движения принимает равновесное значение не более 1 раза.
В ряде случаев переходный процесс носит более сложный – колебательный характер. Классический пример колебательного процесса, возникшего в электрическом контуре, содержащей индуктивность z, емкость С и активное сопротивление R. Если конденсатор заряженный, то разность потенциалом U, то он разряжаться будет через индуктивность и сопротивление, то ток i=
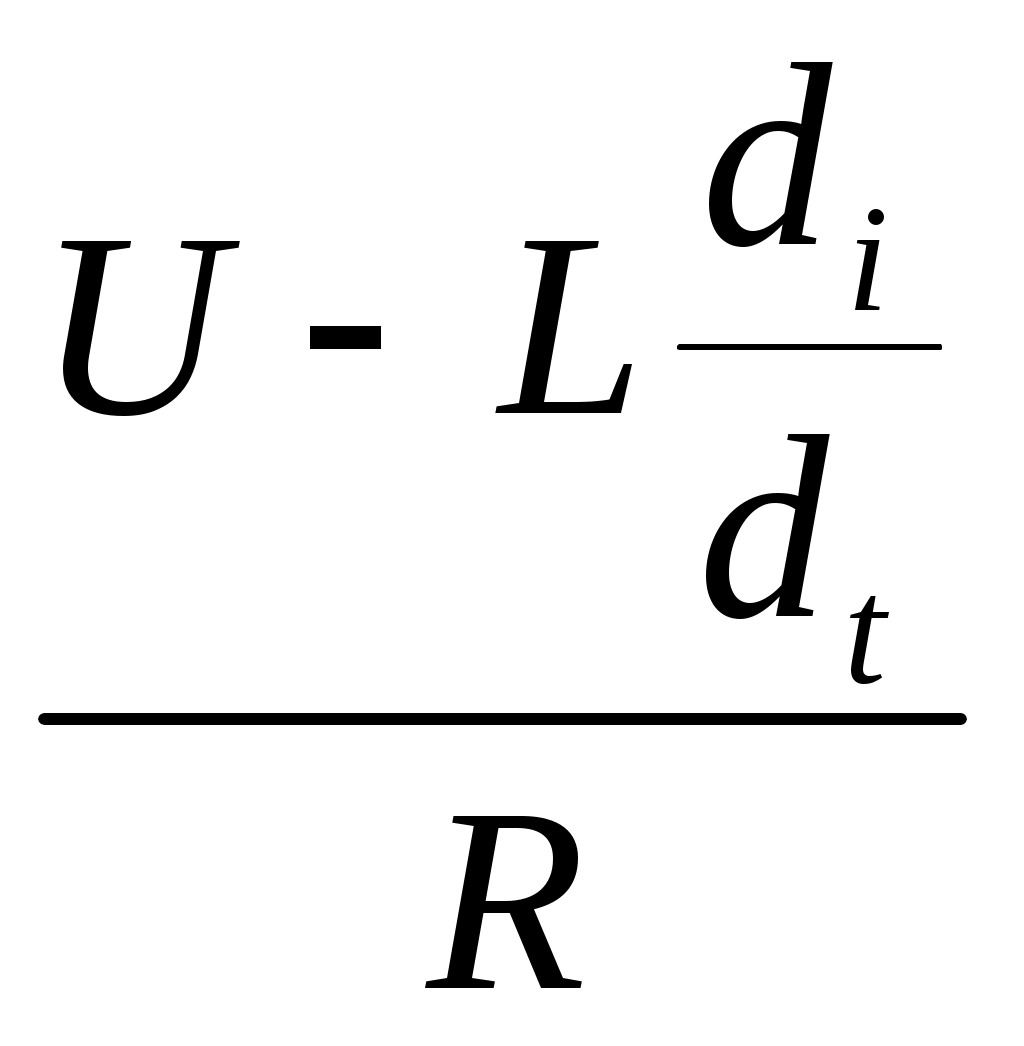.Устойчивость системы
Под устойчивостью или стабильностью системы в широком смысле понимается свойство системы возвращаться в некоторое установившееся состояние или режим после нарушения какими либо внешними или внутренними факторами.
Система может характеризоваться весьма сложным поведением, непрерывно изменятся, но при этом некоторые ее параметры могут сохранять постоянные значения. В таком случае можно говорить об устойчивости системы относительно именно этих параметров.
Например, исследуя процессы в колебательном контуре, было установлено, что не зависимо от начальных значений напряжения и тока, независимо от того имеет ли место затухающие или незатухающие колебания, частота их в данном контуре всегда остается неизменной и определяется параметрами контура. Это дает права назвать колебательный контор системой устойчивой относительно частоты собственных колебаний.
По значению к понятию устойчивости близки понятии равновесия и стационарности (состояния равновесия, стационарный процесс). Однако эти понятия имеет более узкий, частный смысл. Таким образом, более узким, частным является и употребляемое иногда понятие устойчивости системы как способности её стремиться из различных начальных состояний к некоторому равновесному, стационарному состоянию.
Основным содержанием теории устойчивости является: исследования влияния возмущающих воздействий на поведения системы, при этом под возмущающими факторами понимают силы обычно неизвестные заранее, которые как следствие своей неопределенности, так и в следствие относительной малости по сравнению с основными силами, не учитываются при описании движений системы.
Другим примером устойчивости поведения системы является ее цикличности.
Цикличным поведением называется такое, когда система при отсутствии возмущений периодически многократно проходит одну и ту же последовательность состояний – устойчивое множество состояний.
Относительно некоторого возмущения действующего на систему, её состояние равновесия (или цикл) может характеризоваться несколькими типами устойчивости.
Если система возвращается в состояние равновесия при любых возможных воздействиях на неё (при любых возмущениях), то равновесия называют абсолютно устойчивым. Например, маятник.
Если система, при возмущениях возвращается в состояние равновесия только из некоторой области, то равновесие называют устойчивой относительно этой области. Здесь примером может быть кирпич, который если чуть-чуть наклонить, то вернется в свое состояние, а если сильно наклонить, то упадет.
Если после воздействия на систему она сохраняет новое состояние, вызванное этим воздействием, то систему называют безразлично устойчивой. Простейшим примером является однородный круглый диск, укрепленный на оси, проходящий через его центр.
Во всех остальных случаях, система является не устойчивой.
В сложных кибернетических системах в зависимости от характера исследуемых задач и типа возмущения предлагается применять различные методы определения устойчивости (критерии устойчивости). Одним из таких методов, получившее широкое распространение, является определение устойчивости предложенным ученым Ляпуновым: предполагается, что некоторый объект (система автоматического управления) описывается системой дифференциальных уравнений.
Устойчивость поведения систем, как правило, является положительным свойством, обеспечивающим их нормальное целенаправленное функционирования и сохранения целостности в экстремальных условиях. Однако, в ряде случаев, устойчивость отражает инертность, косность системы, ограничивающую возможность управления ими.
Устойчивость является свойством всей системы в целом, а не в какой либо отдельной её части. Система, состоящая из нескольких устойчивых подсистем, может оказаться неустойчивой и наоборот: при объединения некоторого количества неустойчивых подсистем, может возникнуть устойчивая система, в зависимости от способа такого объединения.
С понятием устойчивости тесно связано понятие гомеостаза или гомеостазиса (от греч гомео – равный, стазис – состояние), применяемое вначале в биологии, где оно обозначало поддержание постоянства существенных параметров организма (температура, давление, состава крови и т.д.). В настоящее время гомеостазисом называют свойство системы, при взаимодействии со внешней средой, сохранять существенные параметры в некоторых заданных пределах.