Министерство образования РФ

Томский Государственный университет

систем управления и радиоэлектроники

КОНТРОЛЬНАЯ РАБОТА

ПО ВЫСШЕЙ математике № 4

Вариант № 4.3


Специальность 220400

21.04.2003

2002г.

1. Найти производные от данных функций:

1. 
   
   
2. 
   
   
3. 
   
   

Решение:

1. 
   
   

2. 
   
   

3. 
   
   

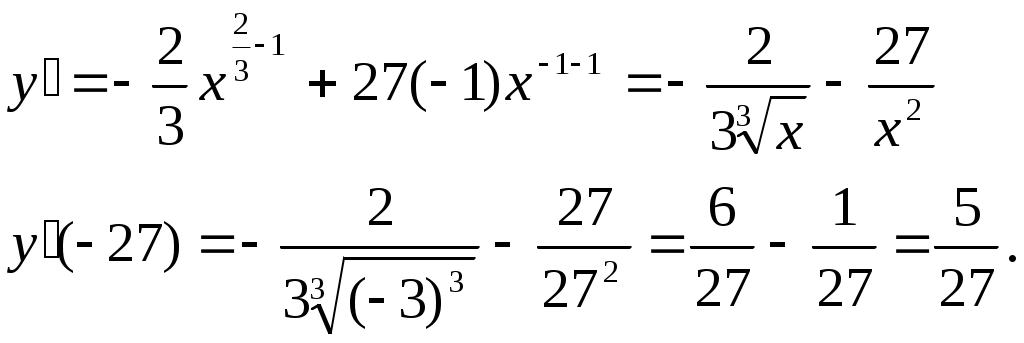
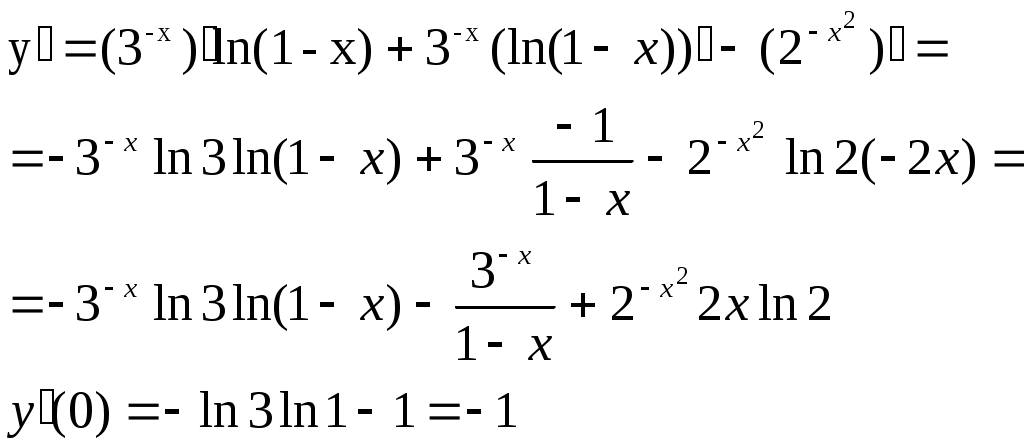
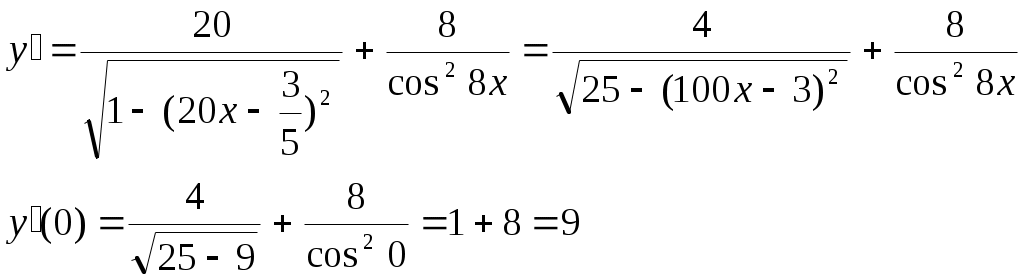
2. Дана функция . Найти:

1. 
   координаты вектора gradu в точке А(-1,3,2);
   
2. 
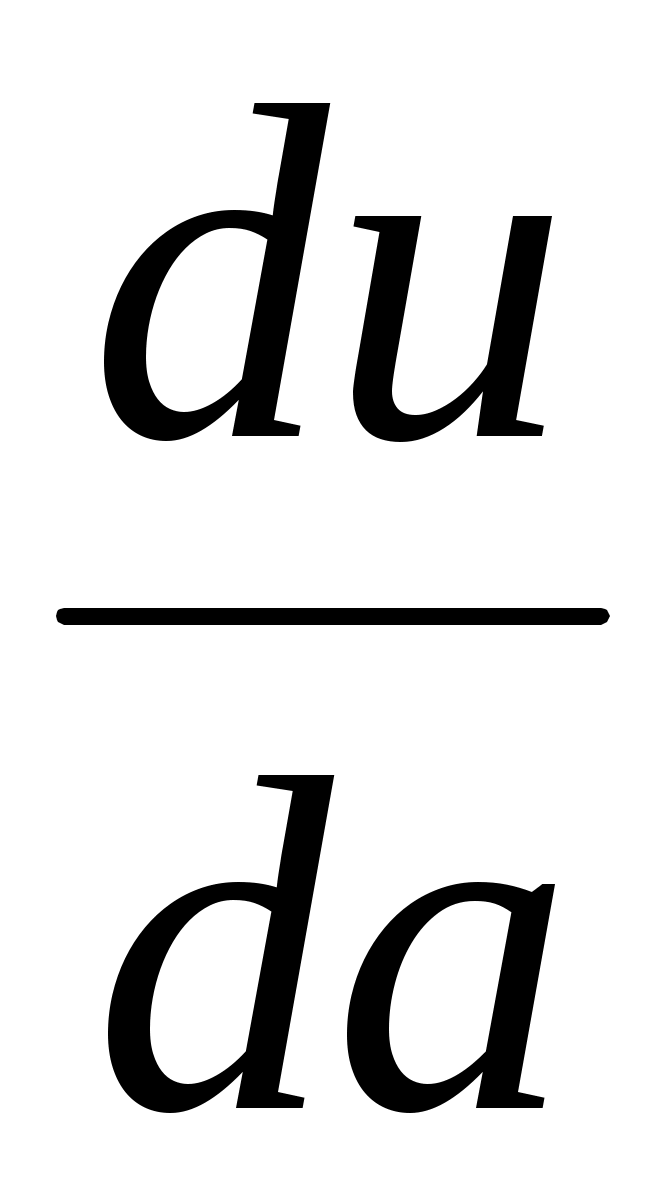   в точке А в направлении вектора а{2,-6,-3}.
   

Решение: Найдем gradu(A)





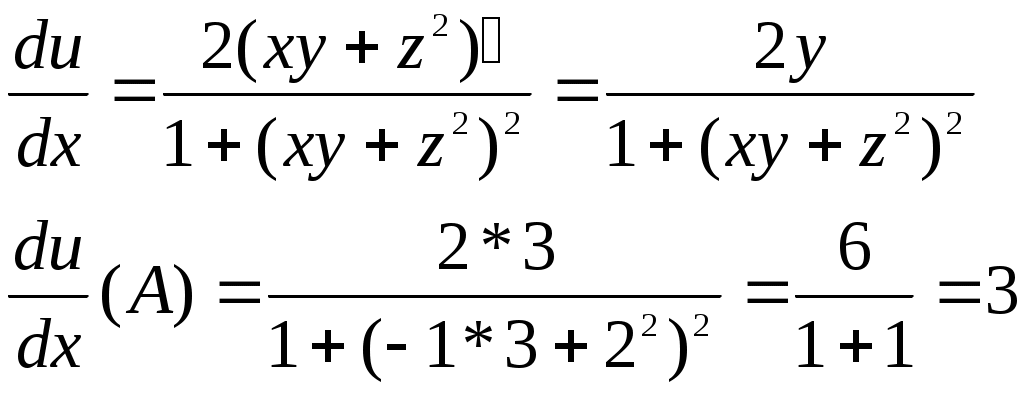
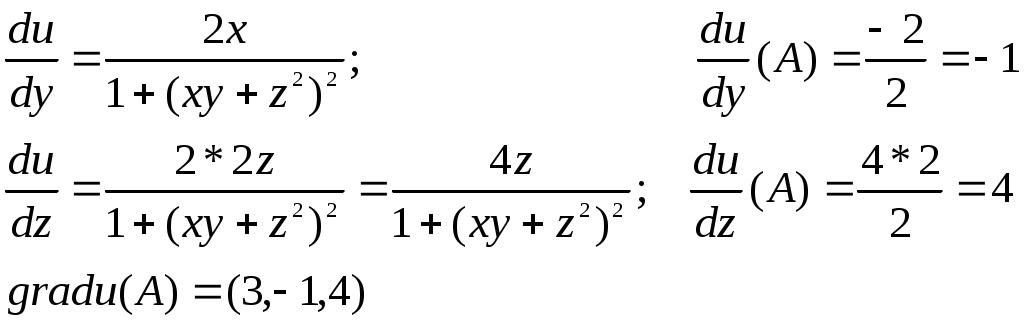
Находим орт вектора а:



По формуле находим



3. Дана функция . Найти . Вычислить

---

.

Решение:



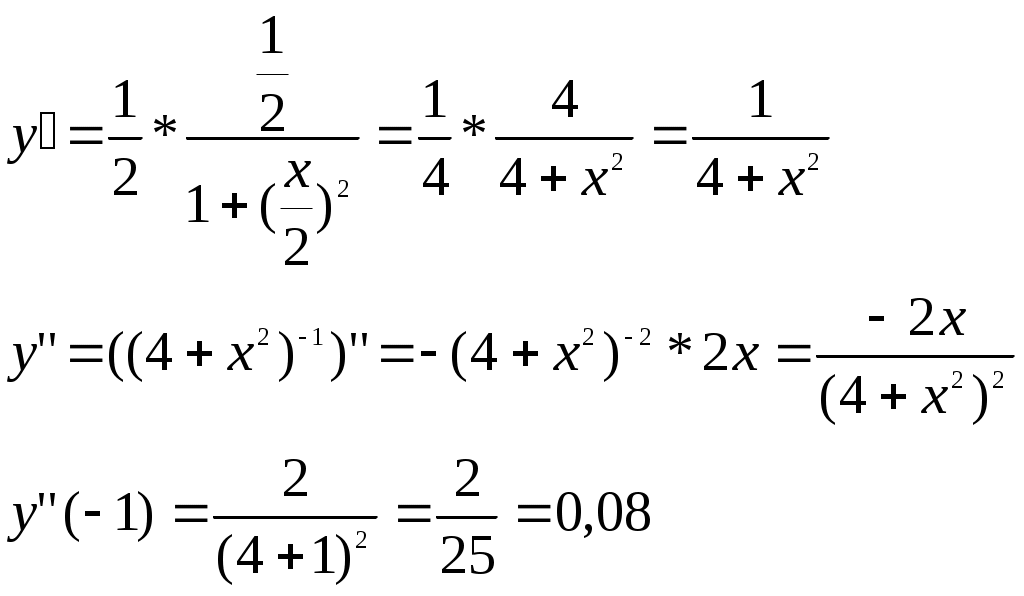
4. Доказать, что функция удовлетворяет уравнению .

Решение: Функцию z(x,y) перепишем в виде . Применяя формулы, найдем



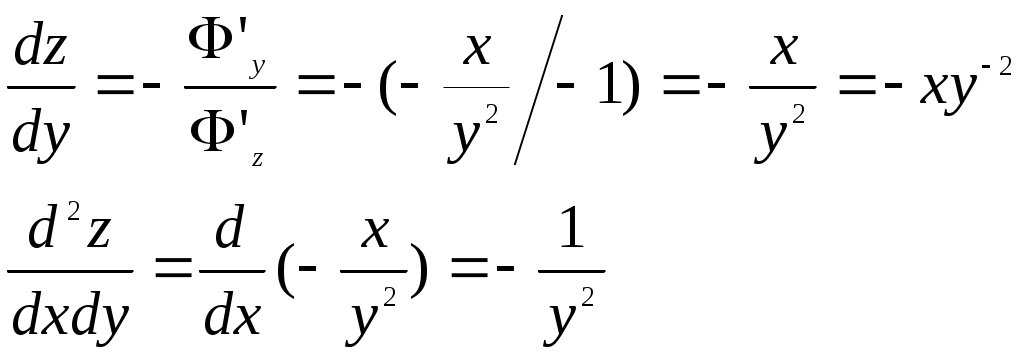
Подставим в данное уравнение



Мы доказали, что функция удовлетворяет уравнению .

5. Найти , если . Вычислить , если .

Решение:



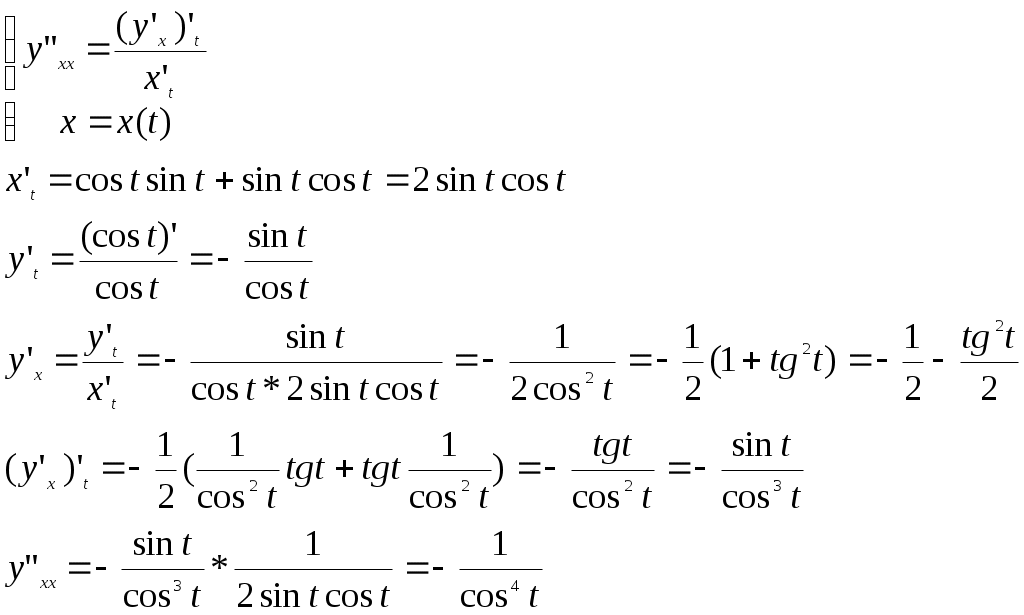
При вторая производная равна:



6. Функция z=z(x,y) задана неявно уравнением

.

Вычислить: а) ; б) .

Решение: Применяя формулы, находим:



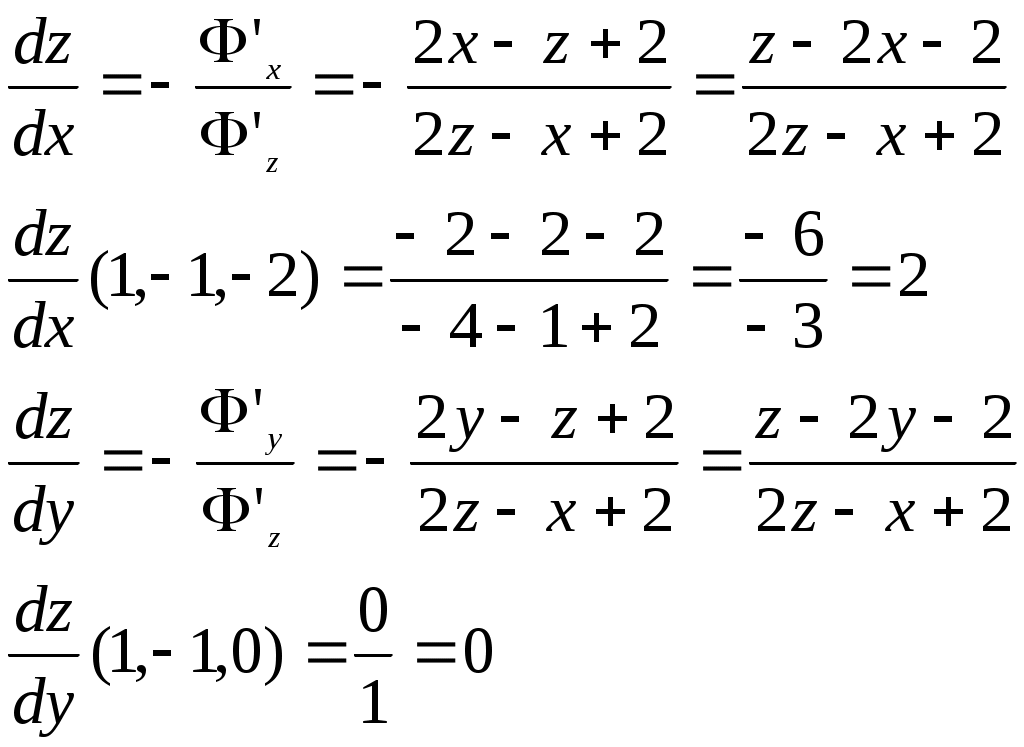
7. На графике функции y=ln2x взята точка A. Касательная к графику в точке A

наклонена к оси

---

OX под углом, тангенс которого равен . Найти абсциссу

точки A.

Решение: у’(x)=тангенсу угла наклона к оси OX касательной к графику функции в точке x. Отсюда:


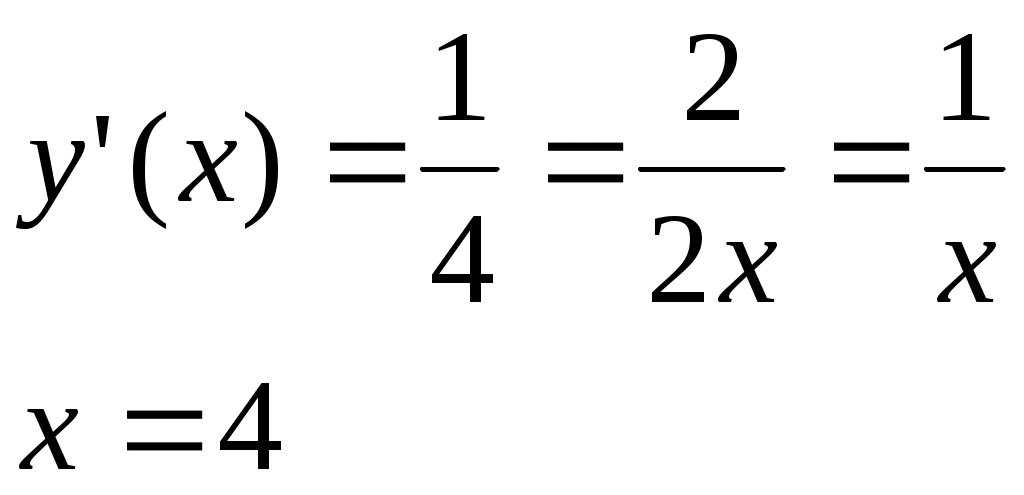
8. Найти dy, если . Вычислить значение dy, если .

Решение:



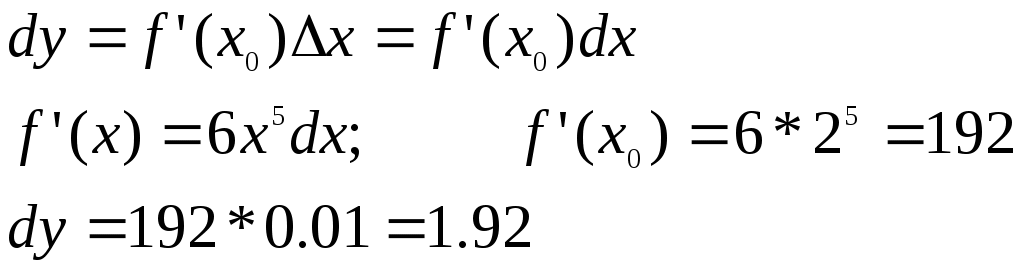
9. Дана функция z=x²+3xy-6y и точки М₀(4;1) и М₁(3,96;1,03). Вычислить zиdz при переходе из точки М₀ в точку М₁(ответы округлять до сотых).

Решение: Находим z



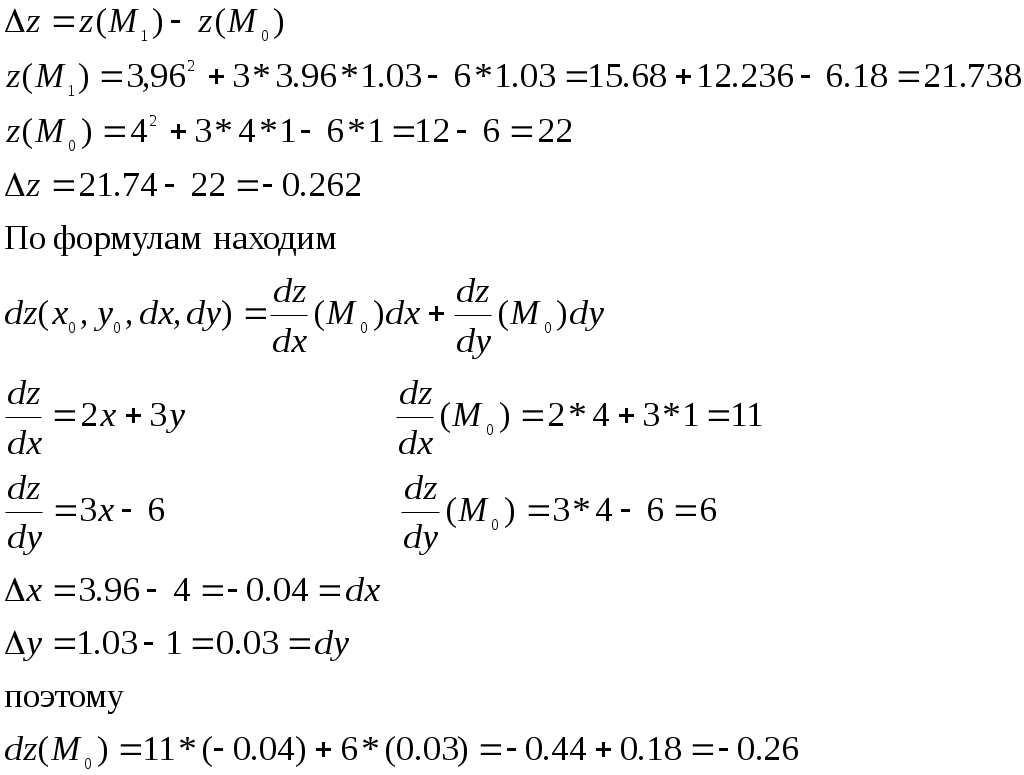
10. Дана функция . Найти ее наибольшее и наименьшее значения на отрезке [0;6].

Решение: Находим критические точки данной функции, приравнивая нулю ее производную.



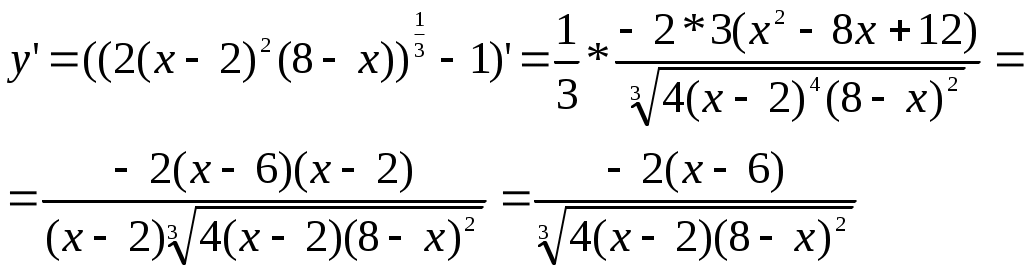
В точке x₁=6 производная равна нулю, в точках x₂ =2 и x₃=8 производная не существует. Точка x₂ =2 является внутренней отрезка [6,0]. Точки x₁ =6 и x₄=0 являются граничными. Вычисляем значение функции во всех этих точках:

y(x₁)=y(6)=3

y(x₂)=y(2)=-1

y(x₄)=y(0)=3

Видим, что наименьшее значение m=-1, оно достигается в точке x₂ =2 , а наибольшее значение – М=3. Оно достигается в граничных точках x₁=6 и x₄=0.

11. Дана функция z=3x²-3xy+y²+4. Найти ее наибольшее и наименьшее значения на замкнутом множестве, ограниченном прямыми x=-1, y=-1, x+y=1.

Решение: Находим стационарные точки из системы:

---

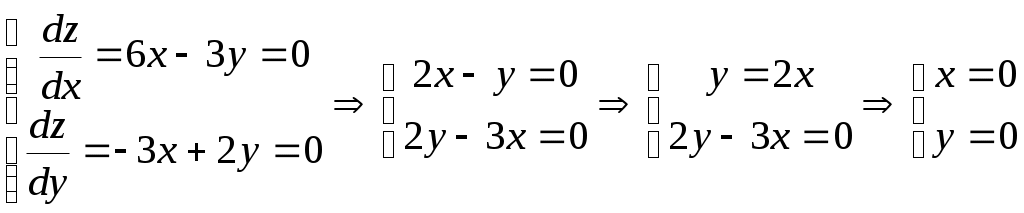
Получаем единственную точку М₁ (0,0). Она лежит внутри данного замкнутого множества.



Точки А(-1,-1); В(-1,2); С(2,-1) – точки пересечения прямых x=-1, y=-1, x+y=1. Вычислим значение функции z(x,y) в этих точках.

Z(-1,-1)=5;

Z(-1,2)=17;

Z(2,-1)=23.

На прямой x+y=1 имеем

Z(x,y)=z(x,1-x)=3x²-3x(1-x)+(1-x)²+4=7x²-5x+5=0

Получили функцию от одного аргумента z₁(x)= 7x²-5x+5. Ищем ее критические точки на [-1,2]:



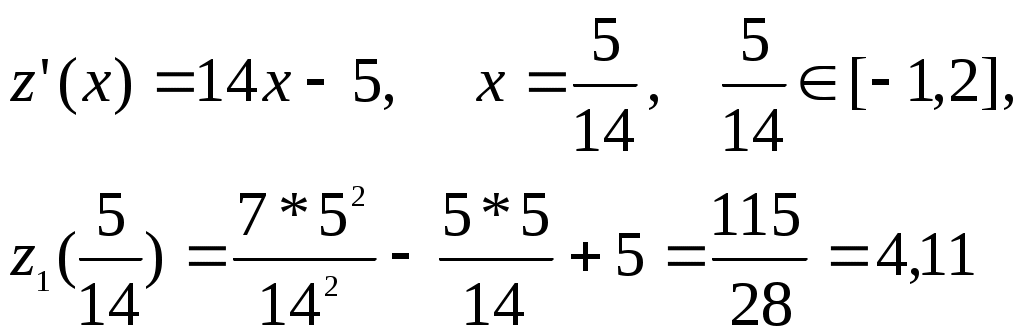
При x=-1 и x=2 приходим к точкам В(-1,2); С(2,-1).

На участке границы x=-1, получаем



Получили функцию z₂(y)=y²+3y+7. Ищем ее наибольшее и наименьшее значение на [-1,2]



При y=-1 и y=2 получаем уже учтенные точки А(-1,-1); В(-1,2).

На участке границы y=-1, получаем



Ищем ее наибольшее и наименьшее значение на [-1,2]



При x=-1 и x=2 получаем уже учтенные точки А(-1,-1); С(2,-1).

Мы нашли следующие значения функции:



Сравнивая их, видим, что наибольшее значение функции в данной области равно 23, оно достигается в точке С(2,-1), а наименьшее равно 4, оно достигается в точке М₁ (0,0).

12. Провести полное исследование функции и начертить ее график.

Решение:

1. 
   функция определена на всей числовой оси, кроме точки x=-2, т.е. ее область определения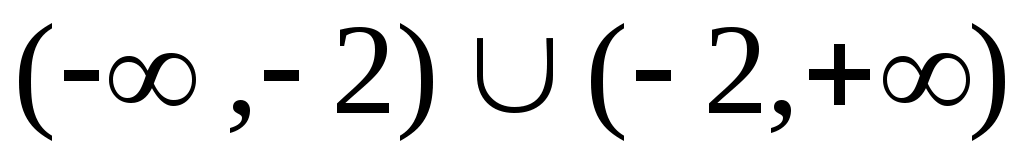 . Область значений – вся числовая ось (-,+). На луче (-,-2) она отрицательна, а на луче (-2,+) – положительна.
   
2. 
   функция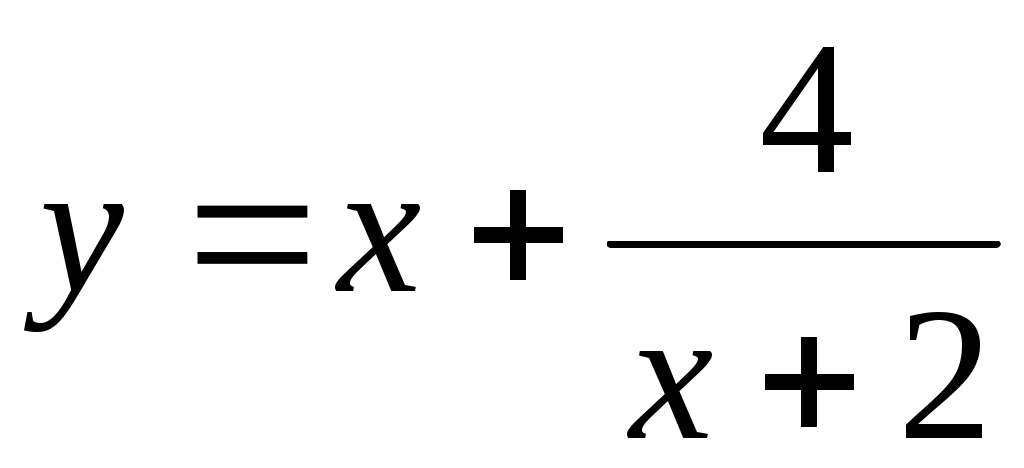 общего вида, не является ни четной ни нечетной.
   
3. 
   данная функция не периодична.
   
4. 
   функция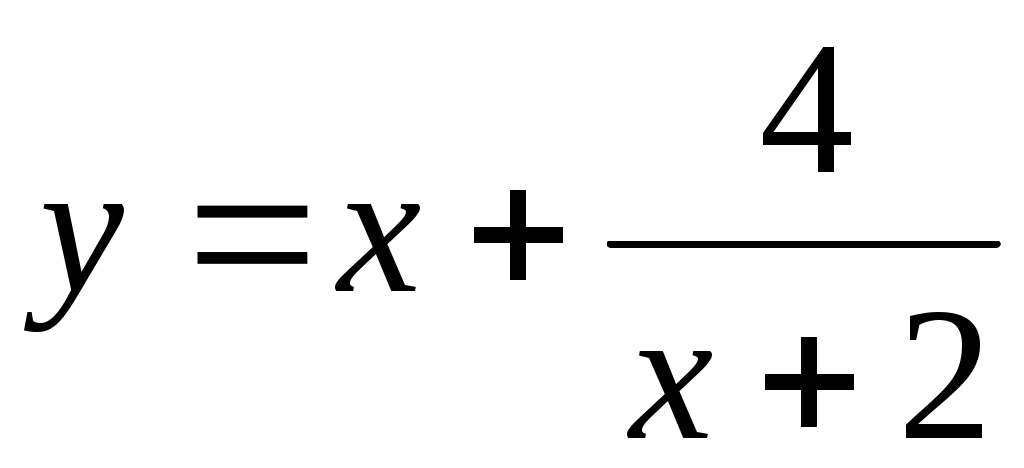 непрерывна всюду,как отношение многочлена, кроме точки x=-2, в которой знаменатель обращается в нуль. Так как 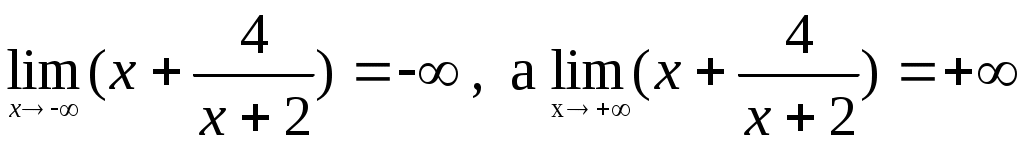, то точка x=-2 – точка разрыва второго рода. Прямая x=-2 – двусторонняя вертикальная асимптота.
   
5. 
   Находим наклонные асимптоты y=kx+b: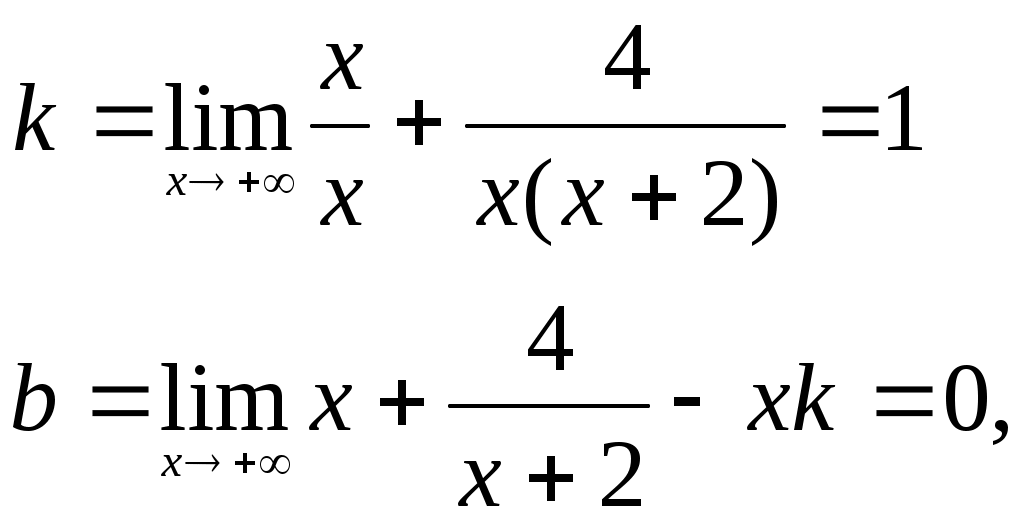 Следовательно, прямая y=x – наклонная двусторонняя асимптота.
   
6. 
   Находим производную: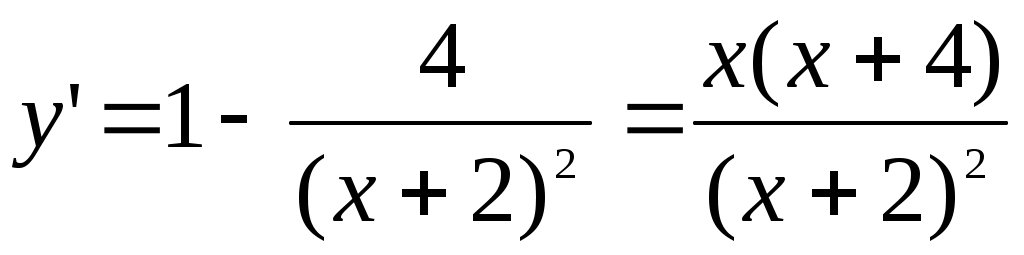 Производная обращается в нуль только в точках x₁=0 и x₂=-4, в точке x₃=-2 производная не существует. На участке (-,-4) производная положительна, следовательно, функция возрастает. На участке (-4,-2) производная отрицательна, следовательно, функция убывает. На участке (-2,0) производная отрицательна – функция убывает, на участке (0,+) производная положительна – функция возрастает. В точке x=-4 имеем максимум 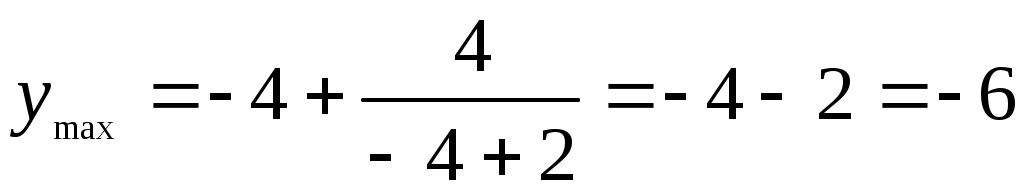. В точке x=0 имеем минимум .
   
7. 
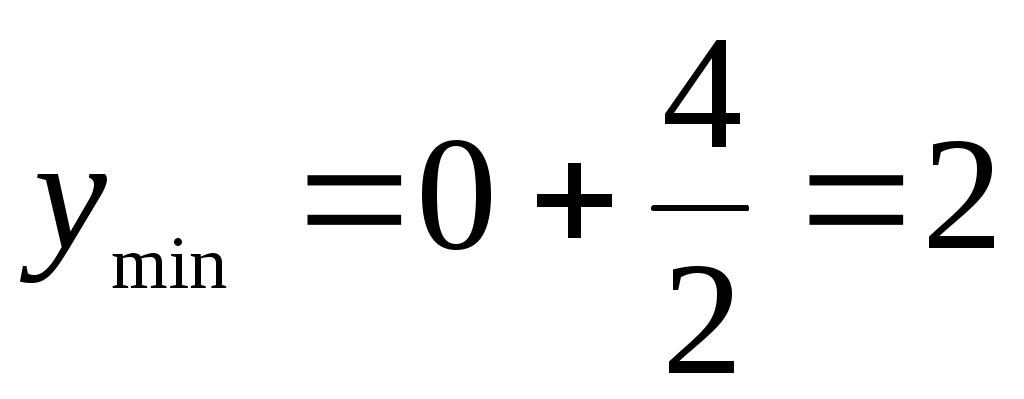   Находим вторую производную: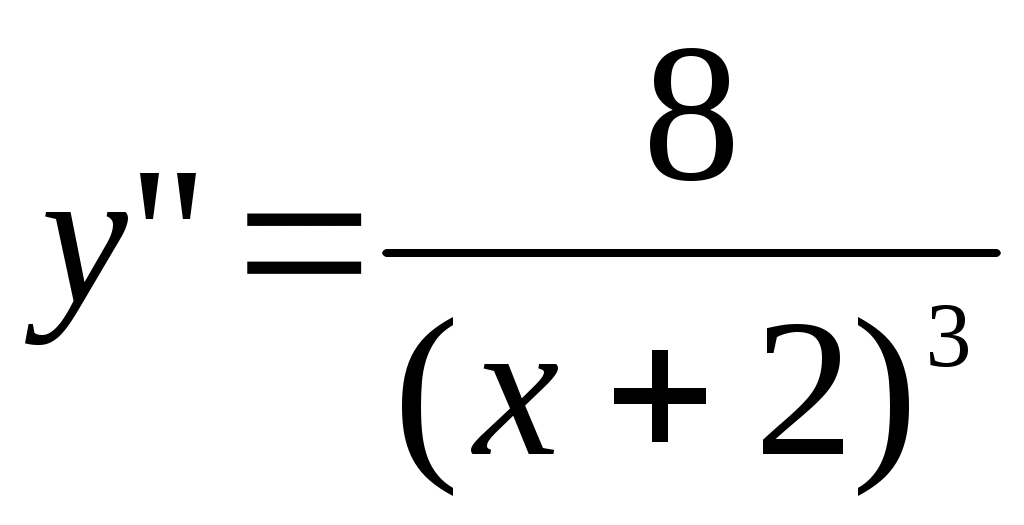 . Вторая производная меняет знак при переходе через точку x=-2. На луче (-,-2) справедливо y”<0, следовательно, график функции выпуклый вверх, на участке (-2,+) имеем y”>0, следовательно, график функции выпуклый вниз.
   

---

Для удобства построения графика полученные данные, а также значения функции в некоторых точках можно занести в таблицы.

X	-10	-6	-4	-2.5	-1.5	-1	0	2	6
Y	-10.5	-7	-6	-10.5	6.5	3	2	3	6.5
			max				min

x	(-,-4)	(-4,-2)	(-2,0)	(0,+)
y	возр.	убыв.	убыв.	возр.

x	(-,-2)	(-2,+)
y	Выпукла вверх	Выпукла вниз

Асимптоты x=-2, y=x.

На основании этих данных строим график функции.

y

6.5

3



-10 -6 -4 -1 2 6 x

---

Смотрите также файлы

• Ашы топыра глді сімдіктері Біржылдытар.docx

• Разработка информационной системы по работе с клиентами организации (на примере ооо стаффджет).pdf

• План работы Школьного методического объединения учителей физической культуры, обж, технологии.docx

• Сущность, формы и функцииисторического знания.pdf

• Муниципальное бюджетное образовательное учреждение Мамхегская средняя общеобразовательная школа 4 Имени Героя Советского Союза Хусена Борежевича Андрухаева.docx