Министерство транспорта Российской Федерации

Федеральное агентство железнодорожного транспорта

Федеральное государственное бюджетное образовательное
учреждение высшего образования

АмИЖТ – филиал ДВГУПС в г. Свободном

Кафедра «Физика и теоретическая механика»

Контрольная работа 2

по дисциплине: Физика
Тема: Электромагнетизм. Оптика. Элементы квантовой физики, физики атома и атомного ядра.
Выполнил:

Дмитриенко Юлия Владимировна

Направление:23.05.04

«Эксплуатация железных дорог»

Шифр: КТ21-ЭЖД(СТ)МТ-461

Проверил: доцент Н.А. Кравцова
Свободный

2022

1. 
   Бесконечно длинный провод с током I =100А изогнут так, как это показано на рис. 1. Определить магнитную индукцию В в точке О. Радиус дуги R= 10 см.
   

Дано: Решение:

I = 100 A R = 10 см = 0,1 м	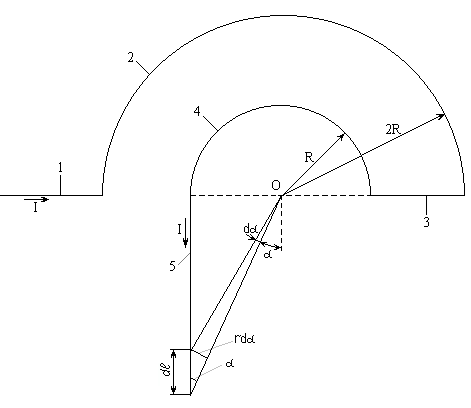Рис. 1
Найти: В ― ?

Будем считать положительным направление вектора магнитной индукции В из плоскости тетради вверх. Найдём магнитную индукцию, создаваемую участками проводника.

Так как точка О лежит на оси участков 1 и 3 проводника, то создаваемая ими магнитная индукция равна нулю: В₁ = В₃ = 0.

Используя выражение для магнитной индукции в центре кругового тока, находим:





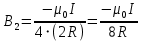
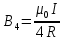
Для определения магнитной индукции В₅, создаваемой пятым участком, воспользуемся законом Био-Савара-Лапласа. Заметим, что вектор dB в точке О направлен из плоскости чертежа вверх. Принцип суперпозиции позволяет для определения В₅ воспользоваться геометрическим суммированием:

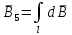(1)

Запишем закон Био-Савара-Лапласа в векторной форме:

---

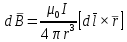
где dB ― магнитная индукция, создаваемая элементом провода длиной dℓ с током I в точке, определяемой радиус-вектором

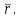
Заметим, что векторы 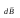от различных элементов тока сонаправлены, поэтому выражение (1) можно переписать в скалярной форме: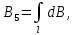



где



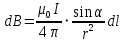
В скалярном выражении закона Био-Савара-Лапласа угол α есть угол между элементом тока 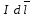и радиус-вектором 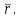Таким образом,

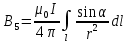(2)

Преобразуем подынтегральное выражение так, чтобы была одна переменная - угол α. Для этого выразим длину элемента проводника dℓ через угол dα:



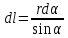
Тогда подынтегральное выражение



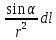
запишем в виде:



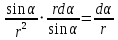
Переменная r также зависит от α, (r = R/sinα), следовательно



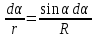
Таким образом, выражение (2) можно переписать в виде:



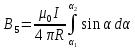
Выполним интегрирование:



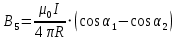
Для 5-го участка α₁ = 0; α₂ = π/2. Тогда:



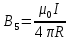
Суммарная магнитная индукция в точке О равна:





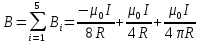
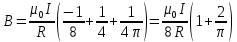
С учётом начальных данных:



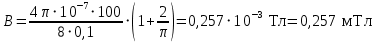
Ответ: В = 0,257 мТл.

2. 
   По двум параллельным проводам длиной l =3м каждый текут одинаковые токи I =500А. Расстояние d между проводами равно 10 см. Определить силу F взаимодействия проводов.
   

Дано: Решение:

ℓ = 3 м I = 500 А d = 10 см = 0,1 м	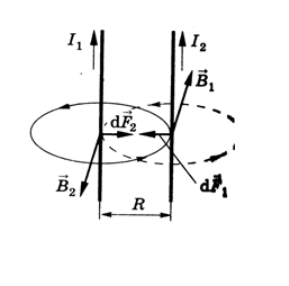Рис. 2
Найти: F ― ?

---

Найдём индукцию, создаваемую первым проводником в точке А:









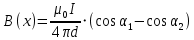
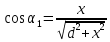
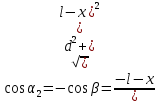
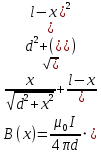
Запишем силу, действующую на элемент длины второго проводника:





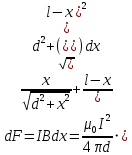
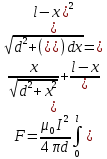
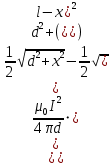
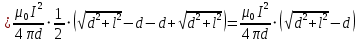
С учётом начальных данных:



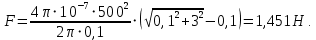
Ответ: F = 1,451 Н.

3. 
   Два иона разных масс с одинаковыми зарядами влетели в однородное магнитное поле, стали двигаться по окружностям радиусами R₁ = 3 cм и R₂ =1,73 см. Определить отношение масс ионов, если они прошли одинаковую ускоряющую разность потенциалов.
   

Дано: Решение:

R1 = 3 см = 0,03 м R2 = 1,73 см = 0,0173 м	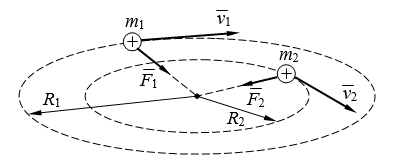Рис. 3
Найти: m1/m2 ― ?

Пройдя одинаковую разность потенциалов, ионы приобрели одинаковую кинетическую энергию:



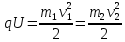
Откуда:

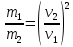(1)

В магнитном поле на каждый из ионов действует сила F_i.



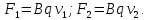
В соответствии со вторым законом Ньютона эти силы равны:



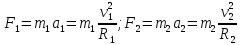
Приравняем выражения для F₁ и отдельно для F₂:





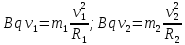
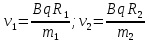
Разделим одно уравнение на другое:



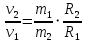
Подставим это выражение в (1):

---

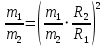
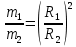
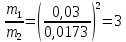
Ответ: m₁/m₂ = 3.

4. 
   Плоский контур площадью S =20см² находится в однородном магнитном поле (В = 0,0З Тл). Определить магнитный поток Ф, пронизывающий контур, если плоскость его составляет угол φ = 60 с направлением линий индукций.
   

Дано: Решение:

S = 20 см2 = 20·10-4 м2 В=0,03Тл φ =60°	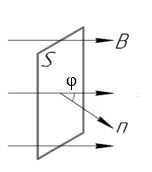Рис. 4
Найти: Ф ― ?

Магнитный поток, пронизывающий виток, находящийся под углом φ к магнитному полю B, равен



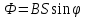
где S – площадь контура.

Подставляем числа:



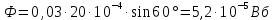
Ответ:

5. 
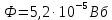
   Между стеклянной пластинкой и лежащей на ней плосковыпуклой линзой находится жидкость. Найти показатель преломления жидкости, если радиус r₃ третьего темного кольца Ньютона при наблюдении в отраженном свете с длиной волны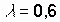  мкм равен 0,82 мм. Радиус кривизны линзы R = = 0,5 м.
   

Дано: Решение:

λ = 0,6 мкм = 6·10–7 м r3 = 0,82 мм = 0,82·10–3 м R = 0,5 м k = 3	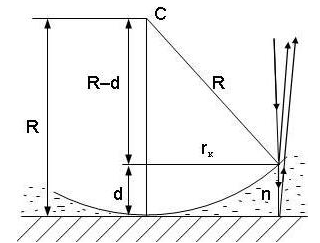Рис. 5
Найти: n ― ?

Из рисунка на основании теоремы Пифагора запишем:



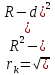
С учётом d< откуда

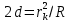(1)

Чтобы получить тёмное кольцо (минимум при интерференции), разность хода должна составлять нечётное число полуволн. С учётом показателя преломления жидкости и того, что при отражении от оптически более плотной среды фаза колебаний изменяется на π, что обуславливает дополнительную разность хода λ/2, запишем:

---

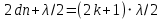
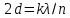(2)

Приравняем правые части равенств (1) и (2):



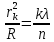
Откуда:



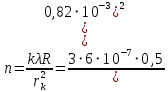
Ответ:

6. 
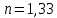
   Какое наименьшее число N_min штрихов должна содержать дифракционная решетка, чтобы в спектре второго порядка можно было видеть раздельно две желтые линии натрия с длинами волн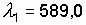 нм и 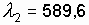нм? Какова длина l такой решетки, если постоянная решетки d = 5 мкм?
   

Дано: Решение:

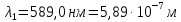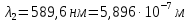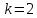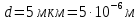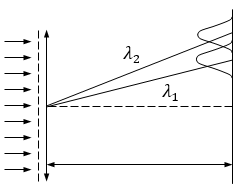	Рис. 6
Найти: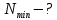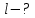

Разрешающая сила дифракционной решетки равна:



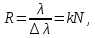
где 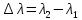. Тогда количество штрихов будет определяться формулой: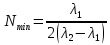



С учётом начальных данных:



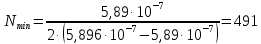
Длина дифракционной решетки:



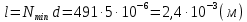
Ответ: ;

7. 
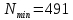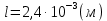
   Вычислить истинную температуру Т вольфрамовой раскаленной ленты, если радиационный пирометр показывает температуру Т_рад= 2,5 кК. Принять, что поглощательная способность для вольфрама не зависит от частоты излучения и равна а_i = 0,35.
   

---

Смотрите также файлы

• азастан Республикасыны Білім жне ылым министрлігі. (министрлікті немесе ведомствоны атауы).doc

• "7 класс".rtf

• 3. Письменно ответьте на вопросы Дайте определение понятию экология.rtf

• Образовательная организация высшего образования(частное учреждение) Международная академия бизнеса и новых технологий мубиНТ Кафедра Экономики и учетноаналитической деятельности.docx

• Целостный педагогический процесс единство обучения и воспитания.docx