ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 12
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
§6. Решение в EXCEL задачи об инвестициях [3].
Рассмотрим задачу Марковица оптимального формирования портфеля ценных бумаг из
рисковых активов, с ограничениями как на минимальный уровень ожидаемой доходности, так и на максимальный размер долей в портфеле (см. пункт Б параграфа §3). Пусть короткие позиции по всем активам запрещены.Напомним введенные выше обозначения:
– средняя ожидаемая доходность -й ценной бумаги, ( называют также эффективностью -й ценной бумаги);
– дисперсия случайной доходности -й ценной бумаги, (среднее квадратическое отклонение называют также риском -й ценной бумаги);
– ковариация дохода от ценных бумаг и
(, );– верхняя граница доли, которую ценные бумаги
-го вида могут составлять в структуре портфеля, .Необходимо сформировать оптимальный портфель ценных бумаг минимального риска при условии, что обеспечивается заданное значение эффективности портфеля (портфель Марковица минимального риска).
Математическая модель такой задачи рассматривалась в §3. Пусть снова () – доля капитала, потраченная на покупку ценных бумаг -го типа (весь выделенный капитал принимается за единицу). С учетом этих обозначений модель задачи формирования портфеля ценных бумаг с минимальной дисперсией (вариацией портфеля) имеет следующий вид:
найти портфель
, минимизирующий дисперсию доходности портфеля ценных бумаг:
при условиях, что:
а) обеспечивается заданное значение эффективности портфеля , т.е.
;
б) доля, которую ценные бумаги
-го вида могут составлять в структуре портфеля, составляет не более , т.е.
,
;в) весь выделенный для инвестиций капитал принимается за единицу, т.е.
;г) короткие позиции по активам запрещены, то есть
.
Получена задача квадратичного программирования, и для нее локальное решение обязательно является глобальным решением.
Пример. Предстоит принять решение о финансовых вложениях свободных денежных средств некоторого предприятия. Рассматриваются три вида ценных бумаг, для которых есть данные о доходах за прошедшие 12 лет: акции компаний AT&T, GM и USS (US Steel). Показатели дохода от акций приводятся ниже:
| Год | Доход от акций, % | ||
| AT&T | GM | USS | |
| 1 | 30,0 | 22,5 | 14,9 |
| 2 | 10,3 | 29,0 | 26,0 |
| 3 | 21,6 | 21,6 | 41,9 |
| 4 | -4,6 | -27,2 | -7,8 |
| 5 | -7,1 | 14,4 | 16,9 |
| 6 | 5,6 | 10,7 | -3,5 |
| 7 | 3,8 | 32,1 | 13,3 |
| 8 | 8,9 | 30,5 | 73,2 |
| 9 | 9,0 | 19,5 | 2,1 |
| 10 | 8,3 | 39,0 | 13,1 |
| 11 | 3,5 | -7,2 | 0,6 |
| 12 | 17,6 | 71,5 | 90,8 |
Необходимо сформировать портфель трех ценных бумаг так
, чтобы минимизировать дисперсию дохода инвестиционного портфеля при условии, что ожидаемый доход составит не менее 15%. Дополнительно должно быть учтено условие, что не более 50% общей суммы свободных средств можно вложить в акции любого одного типа. Кроме того, доли в портфеле должны быть неотрицательными (запрет коротких позиций).
Численное моделирование. На основе исходных данных проведем оценку доходности (эффективности) ценных бумаг (функция = СРЗНАЧ инструмента Мастер функций EXCEL): (рис. 10).
.Для оценки ковариации дохода от ценных бумаг воспользуемся инструментом Ковариация в надстройке Анализ Данных (см. матрицу ковариаций на рис. 10).
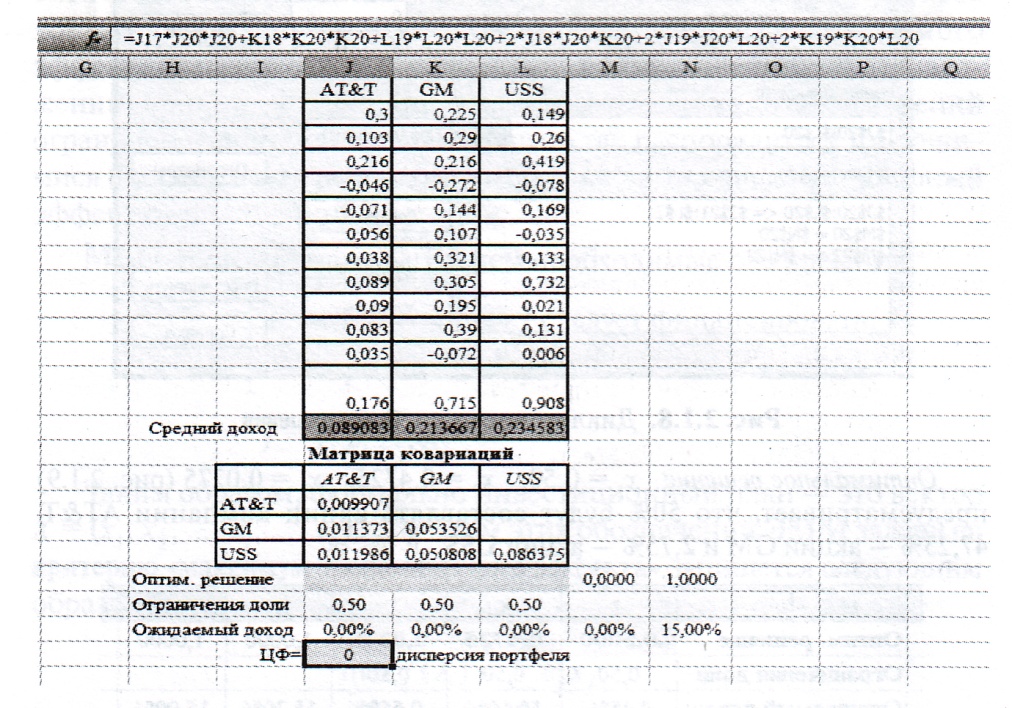
Рис. 10. Рабочий лист
Обозначим в EXCEL переменные
через 
, соответственно 
− через 
.Тогда задача оптимального формирования портфеля ценных бумаг имеет вид:
при ограничениях:
Получение решения. Проведем оптимизацию средствами надстройки Поиск решения.
Рабочий лист может быть подготовлен в виде, представленном на рис. 10. Диалоговое окно, отвечающее приведенному рабочему листу, показано на рис. 11.
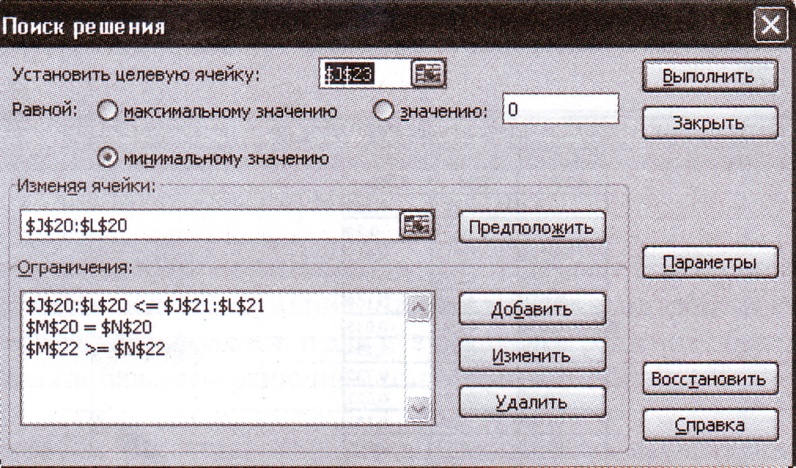
Рис. 11. Диалоговое окно Поиск решения
Оптимальное решение
(см. рис. 12) предусматривает, что 50% будут составлять акции компании AT&T; 47,25% – акции GM и 2,75 – акции USS.
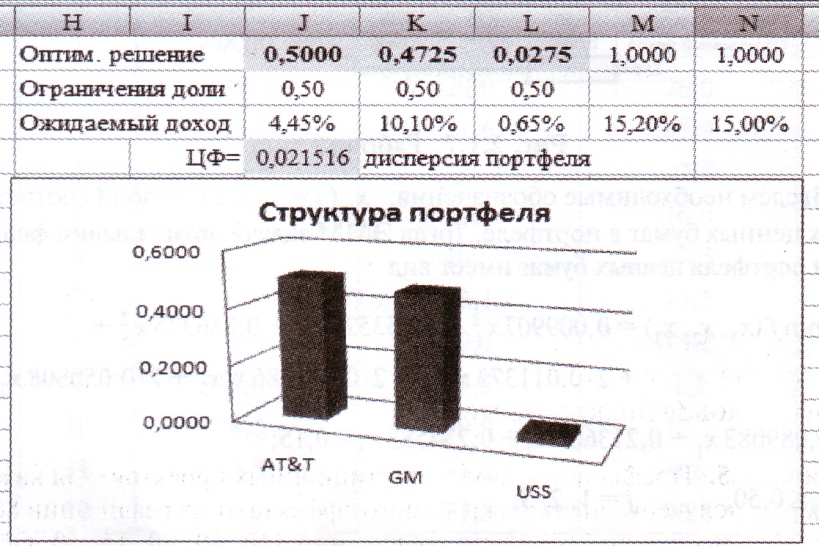
Рис. 12. Результаты решения в EXCEL
Ожидаемый годовой доход равен 15,2%, вариация годового дохода портфеля составляет примерно 0,0215. Таким образом, среднее квадратическое отклонение (с.к.о.) равно 14,67%.
В предположении о нормальном распределении дохода инвестиционного портфеля со средним значением 15,2% и с.к.о. 14,67% с вероятностью 95% можно ожидать, что в следующем году такой портфель будет давать доход от −14,14 до +44,54% (правило «двух сигм»).