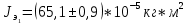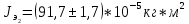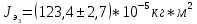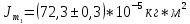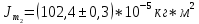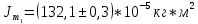Файл: Отчет по лабораторной работе 7 "Определение момента инерции твердых тел с помощью маятника Максвелла".docx

ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ


МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»

Кафедра общей и технической физики

ОТЧЕТ

по лабораторной работе №7

“Определение момента инерции твердых тел с помощью маятника Максвелла”
Выполнил: студент группы НТС– 22 ______________ / Адальшин Д.К. /

(подпись) (Ф.И.О.)
Дата: _________________
Проверил: _____________ / /

(подпись) (Ф.И.О)

Санкт-Петербург

2023

Цель работы - изучение маятника Максвелла и определение с его помощью момента инерции твердых тел.
Краткое теоретическое содержание

Явление, изучаемое в работе: Инерции

Определение основных физических понятий, объектов, процессов и величин:

Инерция - свойства тел сохранять состояние покоя или равномерного прямолинейного движения.

Момент инерции тела относительно оси вращения - это скалярная величина, равная сумме произведения масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси.

Маятник Максвелла представляет собой однородный диск, через центр которого проходит металлический стержень . К концам этого стержня прикреплены две нити. Они тщательно, виток к витку, наматываются на стержень в направлении от его конца к диску. При этом диск на стержне поднимается вверх. Если не удерживать диск в верхнем положении, то возникает поступательное движение маятника вниз и его вращательное движение вокруг оси симметрии. Вращение, продолжаясь по инерции в низшей точке движения (когда нити уже размотаны), приводит вновь к наматыванию нити на стержень. Диск снова поднимается вверх и движение повторяется, т.е. возникают колебания.

Колебания - это процессы (движения или изменения состояния), в той или иной степени, повторяющиеся во времени.

---

Законы и соотношения, описывающие изучаемые процессы и пояснения к физическим величинам и их единицы измерения:

Момент инерции твердого тела в данной работе рассчитывается по формуле, выведенной на основе закона сохранения энергии.



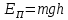
- полная энергия маятника в начальном положении (при закреплении его на верхнем кронштейне).



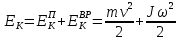
- полная энергия маятника в нижней точке движения, равная сумме кинетических энергий поступательного и вращательного движений.

 - линейная скорость поступательного движения маятника; [ ] = м/с

 - угловая скорость вращательного движения маятника; [] = рад\с

J - момент инерции; [J] = кг м_­­­²

m - масса маятника; [m] = кг

Схема установки

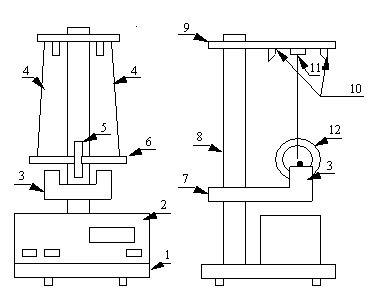
рисунок 1 Схема установки

1. Основание установки.

2. Электронный секундомер.

3. Фотоэлектрический датчик.

4. Нити.

5. Диск маятника.

6. Ось маятника.

7. Подвижный нижний кронштейн.

8. Колонка.

9. Верхний кронштейн, прикрепленный неподвижно к колонке 8.

10. Электромагнит.

11. Фотоэлектрический датчик.

12. Сменные кольца.

Основные расчетные формулы

1. 
   Момент инерции тела: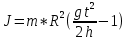
   

m - масса маятника, кг

R - радиус оси маятника, м

g - ускорение свободного падения, = 9,8 м/с²

t - среднее значение времени падения маятника, с

h - длина нити маятника, м

2. 
   Масса маятника: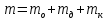
   

m_о - масса оси маятника, кг

m_д - масса диска, кг

m_к - масса кольца, кг

3. 
   Среднее значение времени падения маятника: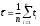
   

---

n – номер опыта

t_i – время падения маятника, с

4. 
   Теоретическое значение момента инерции маятника: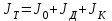
   

J₀ - момент инерции оси маятника, кг/м²

J_д - момент инерции диска, кг/м²

J_к - момент инерции кольца, надетого на диск, кг/м²

5. 
   Момент инерции оси маятника: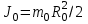
   

R_o – радиус оси маятника, м

m_о - масса оси маятника, кг

6. 
   Момент инерции диска: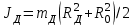
   

R_д - радиус диска, м

R_o – радиус оси маятника, м

m_д - масса диска, кг

7. 
   Момент инерции кольца, надетого на диск: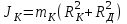 /2
   

R_к - радиус кольца, м

R_д - радиус диска, м

m_к - масса кольца, кг
Формулы погрешностей косвенных измерений

1. 
   Средняя квадратичная погрешность для полученного экспериментально значения момента инерции:
   

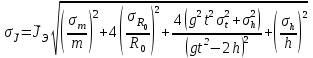
Таблицы

Таблица 1 Погрешности приборов

№	Название прибора	Пределы измерений	Число делений	Цена деления	Класс точности	Абсолютная приборная погрешность
1	Секундомер (электронный)	99,999 с	-	0,001 с	-	0,001 с
2	Шкала длины	430 мм	430	1 мм	-	1 мм
3	Весы (электронные)	5000 г	-	1 г	-	0,5 г
4	Штангенциркуль	300 мм	3000	0,05 мм	-	0,05 мм

---

Таблица 2 Время движения колец 1,2,3

Физическая величина	t1	t2	t3
Единица измерения № опыта	c	c	c
1	2,048	2,028	2,311
2	1,959	2,047	2,197
3	2,002	2,123	2,223
4	1,962	1,979	2,182
5	1,974	2,036	2,144
6	1,960	2,028	2,123
7	2,040	2,140	2,082
8	1,944	2,160	2,095
9	2,031	2,056	2,164
10	2,042	2,094	2,072

Пример вычислений

1. 
   Исходные данные:
   

Кольцо №1:

m = 263,5 г

d = 105 мм

Кольцо № 2:

m = 394 г

d = 105 мм

Кольцо № 3:

m = 523 г

d = 105 мм

Ось:

m_о = 32,2 г

D_о = 10 мм

Диск:

m_д = 124 г

D_д = 86 мм

2. 
   Погрешности прямых измерений:
   

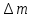= 0,5 г

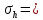1 мм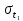

= 0,013 c

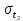= 0,018 c

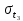= 0,023 c

3. 
   Вычисления:
   

1. 
   Теоретические значения моментов инерции:
   

2. 
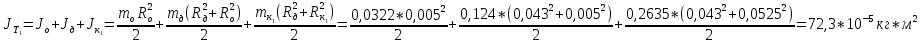
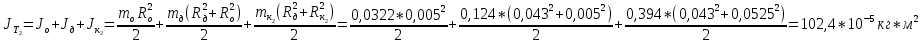
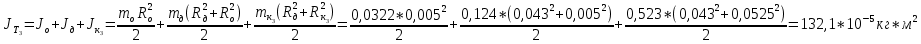
   Масса для экспериментальных значений:
   

---

3. 
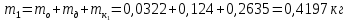
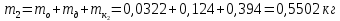
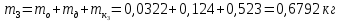
   Среднее время:
   

4. 
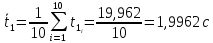
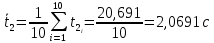
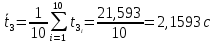
   Экспериментальные значения моментов инерции:
   

5. 
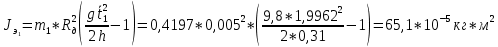
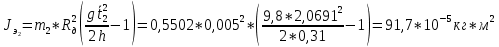
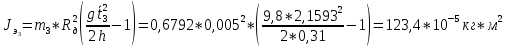
   Вычисление косвенных погрешностей экспериментальных моментов инерции:
   

6. 
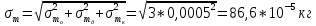
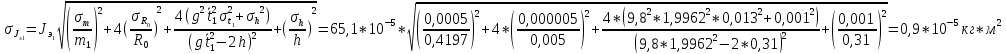
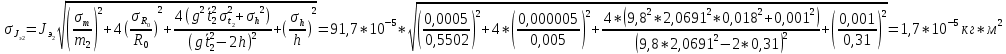
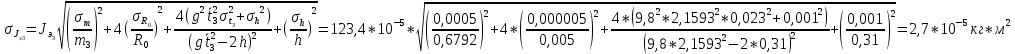
   Вычисление косвенных погрешностей экспериментальных моментов инерции:
   

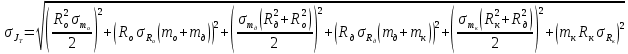
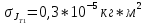
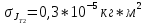
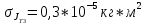
График

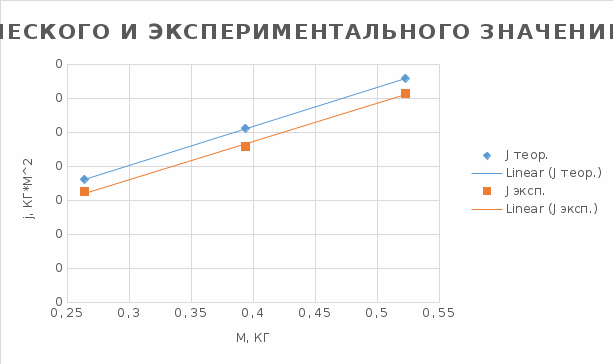рисунок 2 Сравнение теоретического и экспериментального значений момента инерции

Результаты

---