1. 
   Цель работы:
   

Изучить методы линеаризации в пространстве состояний. Линеаризовать 2 дифференциальных уравнения и проверить решение в программной среде Matlab. (18 вариант)

2. 
   Ход работы
   

Даны 2 дифференциальных уравнения:





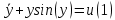
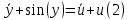
Для дифференциального уравнения (1)

Сначала введем переменные состояния:



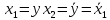
Дальше запишем ситему нелинейных уравнений состояний:



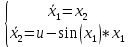
Якобианы системы примут вид:



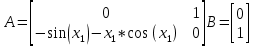
Выберем первую рабочую точку:



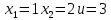
Тогда



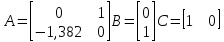
Выберем вторую рабочую точку:



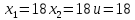
Тогда



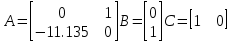
Далее проверим решение при помощи Simulink:



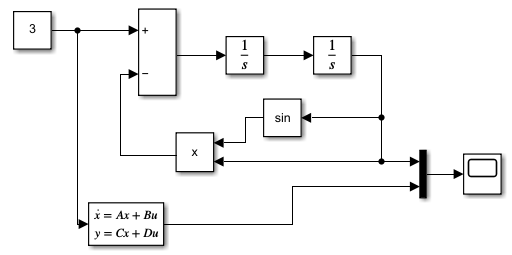
Рисунок 1 – Блок-схема для проверки решения 1-го уравнения



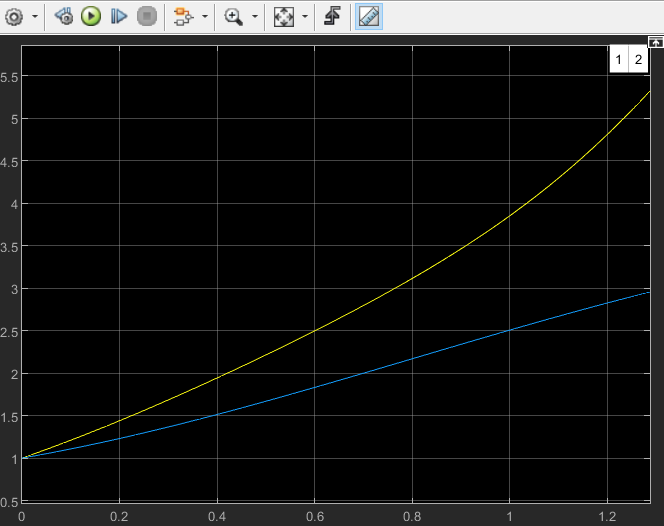
Рисунок 2 - Переходные процессы нелинейной и линеаризованной систем в первой рабочей точке



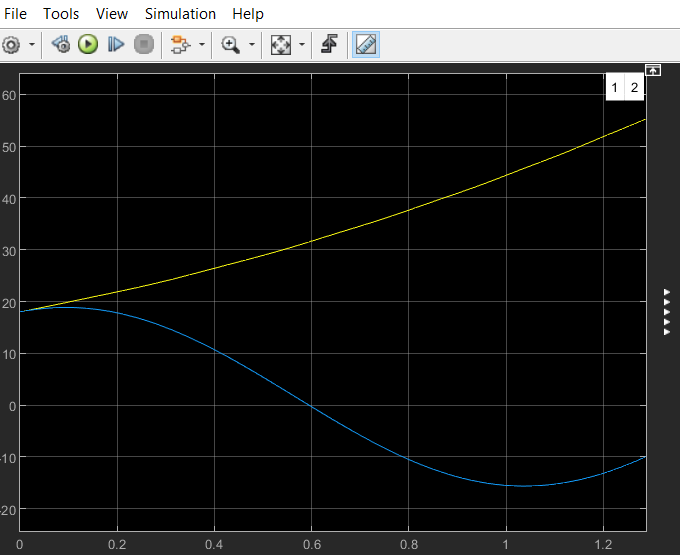
Рисунок 3 - Переходные процессы нелинейной и линеаризованной систем во второй рабочей точке

Для дифференциального уравнения (2)

Сначала введем переменные состояния:



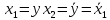
Дальше запишем ситему нелинейных уравнений состояний:



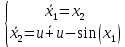
Якобианы системы примут вид:



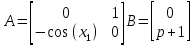
Выберем первую рабочую точку:

---

Тогда



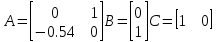
Выберем вторую рабочую точку:



Тогда



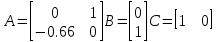
Далее проверим решение при помощи Simulink:



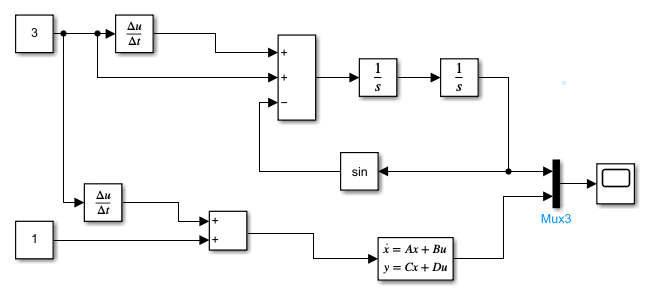
Рисунок 4 - Блок-схема для проверки решения 2-го уравнения



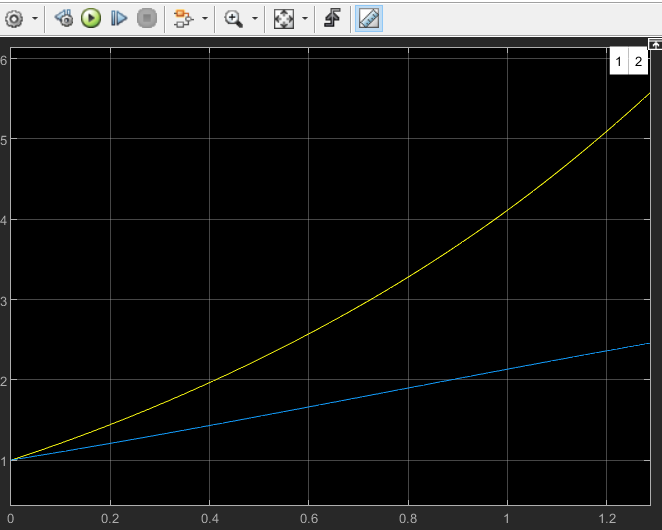
Рисунок 5 - Переходные процессы нелинейной и линеаризованной систем в первой рабочей точке



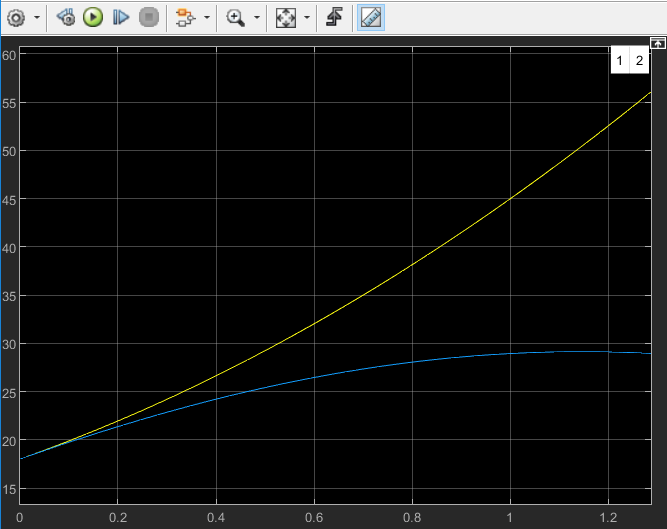
Рисунок 6 - Переходные процессы нелинейной и линеаризованной систем во второй рабочей точке

3. 
   Вывод
   

В ходе выполнения работы была произведена линеаризация 2-х дифференциальных уравнений в пространстве состояний в 2-х рабочих точках.

---

Смотрите также файлы

• Классификация абзоу по способам подготовки к захвату.pdf

• Лекция 1 Тема Общественный сектор экономики Вопросы Общественный сектор. Ресурсы общественного сектора.doc

• Разветвляющиеся алгоритмы Домашняя работа 1 по дисциплине Алгоритмизация и программирование.docx

• А 17 (vii), 16 (VI), 15 (VI), 14 (IV) топ элементтері жне оларды осылыстары блімі бойынша жиынты баалау.docx

• Финансовый поток.docx