МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИИЙСКОЙ ФЕДЕРАЦИИ

Тульский филиал

федерального государственного бюджетного образовательного учреждения высшего образования

«РОССИЙСКИЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ имени Г.В.ПЛЕХАНОВА»

(Тульский филиал РЭУ им. Г. В. Плеханова)

Кафедра финансов и информационных технологий управления
Контрольная работа 5

по дисциплине «Математический анализ»

на тему: «Функции многих переменных»

Выполнила:

студент(ка) 1 курса группы №1 очной формы

обучения направления 38.03.01 «Экономика»

Москвичева Алена Дмитриевна

Проверил: доктор технических

наук Юдин Сергей Владимирович

Тула, 2022

Группа # 5 Вариант # 12

# 1. Найти частную производную функции u по s в точке t= 7 , s=-6 , если u=-1 x^2+-1 xy+-6 y^2, x= 9 t+ 9 s, y= 9 t- 9 s.

# 2. Найти частную производную функции u по t в точке t= 8 , s=-10 , если u=ln(1+ 6 x^2+ 9 y^2), x=ts, y=t+s.

# 3. Найти частную производную функции z по u в точке u= 8 , v= 9 , если z= 2 /(1+x^2+y^2)+ 4 (x^2+y^2), x=ln(uv), y=u+v.

# 4. Найти экстремумы функции z=-9 x^2+-4 xy+-6 y^2+ 0

# 5. Найти экстремумы функции z=(-4 x+ 6 y)EXP( 2 xy)

# 6. Найти экстремумы функции z= 3 x^2+ 3 xy+ 9 y^2 при условии, что 6 x^2+ 8 y^2=1.

# 7. Найти минимальное и максимальное значения функции z= 9 x^2+-8 xy+-10 y^2 в области |x|+|y|<=1

# 8. Найти минимальное и максимальное значения функции z= 2 x+ 2 y+ 2 в области 5 x^2+ 4 y^2<=1.

# 9. Найти минимальное и максимальное значения функции z= 5 x^2+-6 y^2 в области (x+-6 )^2+y^2<=4.

№ задания	Ответ
1	11502
2	0,248823
3	140,27577
4	экстремумов нет.
5
6
7	zmax 3 , zmin -10
8	А(0,298; 0,373; 3,342) (min); В(-0,298; -0,373; 0,658) (max)
9	zmax=32,92591 , zmin 0

---

# 1. Найти частную производную функции u по s в

точке t=7 , s=-6 , если ,

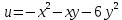x=9 t+ 9 s, y=9 t- 9 s.
Решение:

Воспользуемся общей формулой:

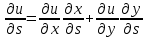
Имеем:
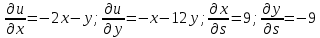
Далее:

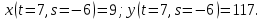
Подставляя полученные результаты в исходную формулу, получаем:



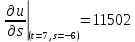
Ответ: 11502
# 2. Найти частную производную функции u по t в

точке t=8 , s=-10 , если ,

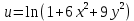x=ts, y=t+s.

Решение:

Решение этой задачи аналогично решению задачи 1.Воспользуемся общей формулой:

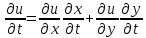
Имеем:
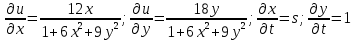
Далее:

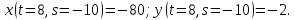
Подставляя полученные результаты в исходную формулу, получаем:



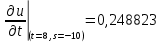
Ответ:0,248823


# 3. Найти частную производную функции z по u в

точке u= 8 , v= 9 , если ,

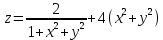x=ln(uv), y=u+v.
Решение:

Снова воспользуемся общей формулой:

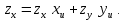
Вычисляем:



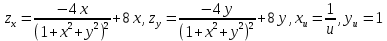
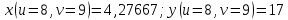
Подставляя полученные выражения в общую формулу, получим:



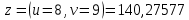
Ответ: 140,27577
# 4. Найти экстремумы функции

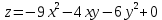
Решение:

1). Найдем стационарные точки, для чего найдем частные производные и приравняем их нулю:

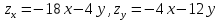
Отсюда получаем систему уравнений: .

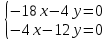Решение этой системы: x=y=0.

2). Исследуем найденную стационарную точку на экстремум, для чего найдем все вторые производные:

---

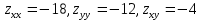
Вычислим параметр

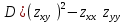
Если D >0 , то экстремум существует, причем, если 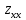 0 , то это точка минимума, если 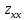" 0 - точка максимума.

Если D  0 , то экстремума нет. В нашем случае D  16  (18)*(-12)  -200 .

Таким образом, экстремум не существует.

Ответ: экстремумов нет.
# 7. Найти минимальное и максимальное значения

функции 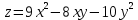в области |x|+|y|<=1

Решение:

Решение этой задачи разбивается на несколько этапов.




1). Находим безусловный экстремум, для чего вычисляем частные производные и приравниваем их нулю:



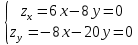
Решение этой системы: x  y  0

Эта точка принадлежит области D:| x |  | y |1 Обозначим z1  z(0;0)  0.

2). Найдем экстремумы функции на границе области D .

Область D является квадратом. В вершинах квадрата линия границы терпит излом, т.е. эти точки являются особыми точками границы. Согласно 56 теории, необходимо в качестве точек, подозрительных на минимум и максимум, использовать все особые точки, как функции, так и границы.

Таким образом, возникает еще четыре подозрительные точки: { M₂ ( 0; 1); z₂ = -10}; { M₃ ( 1; 0); z₃ = 3}; { M₄ ( 0;-1); z₄ = -10}; { M₅ (-1; 0); z₅ = 3}.

Исследуем гладкие участки границы на условный экстремум.

1. 
   В первом квадранте уравнение границы имеет вид x  y 1.
   

Подставим это уравнение в выражение для функции:



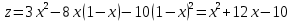
Дифференцируем и приравниваем производную нулю:





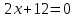
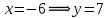
Очевидно, что точка M₆( -6;7)  не принадлежит рассматриваемому квадрату, поэтому мы исключаем ее из рассмотрения.

---

2. 
   Во втором квадранте уравнение границы имеет вид:  x  y 1 Подставим это уравнение в выражение для функции:
   

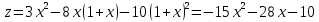
Дифференцируем и приравниваем производную нулю:



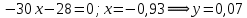
Очевидно, что точка M₇ ( -0,93; 0,07)  принадлежит рассматриваемому квадрату.

3. 
   В третьем квадранте уравнение границы имеет вид:  x  y 1 Подставим это уравнение в выражение для функции:
   

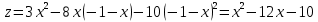
Дифференцируем и приравниваем производную нулю:



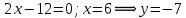
Очевидно, что точка M₈ ( 6; -7)   не принадлежит рассматриваемому квадрату, поэтому мы исключаем ее из рассмотрения.

d) В четвертом квадранте уравнение границы имеет вид: x  y 1.

Подставим это уравнение в выражение для функции:



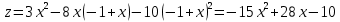
Дифференцируем и приравниваем производную нулю:



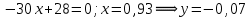
Очевидно, что точка M₉ ( 0,93; -0,07)  принадлежит рассматриваемому квадрату.

3). Найдем теперь максимальное и минимальное значения исследуемой функции в области | x |  | y |1 .

Для этого рассмотрим все полученные точки, принадлежащие этой области и выберем из них точки с минимальным и максимальным значениями.

Такими точками являются точки M2 и M4 (минимум), точки M3 и M5 (максимум),М₇ и М₉.

Ответ: z_max 3 , z_min -10
# 8. Найти минимальное и максимальное значения

функции z=2 x+2y+ 2 в области 5 x^2+ 4 y^2<=1.

Решение:

Очевидно, что безусловного экстремума эта функция не имеет, следовательно, экстремум может достигаться только на границе.

Для отыскания экстремума на границе следует использовать метод неопределенных множителей Лагранжа.

Уравнение границы имеет вид: .

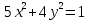Функция Лагранжа:

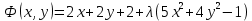
Находим ее производные и приравниваем их нулю:



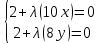
Отсюда:

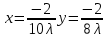
Подставим в уравнение связи:

---

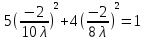
или

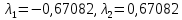
Тогда: x₁ =0,298143 ; y₁ =0,372678 ; z₁ =3,341642

x₂ =-0,298143 ; y₂ =-0,372678 ; z₂ =0,658358

Ответ: А(0,298; 0,373; 3,342) (min); В(-0,298; -0,373; 0,658) (max)
# 9. Найти минимальное и максимальное значения

функции z=5 x^2-6 y^2 в области (x-6 )^2+y^2<=4.

Решение:

1). Найдем безусловный экстремум:

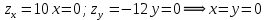,z(0,0)=0.

Эта точка принадлежит отмеченной выше области.

2). Найдем условный экстремум.

Функция связи:

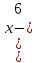
Функция Лагранжа:

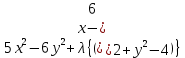
Система уравнений:

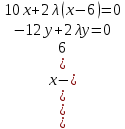
Второе уравнение дает нам y  0 или   6.

y  0 : при подстановке в уравнение связи даст x  4 и x  8.

Таким образом, имеем еще две точки:{ M₂ (4;0) , z₂  80};{ M₃ ( 8;0), z₃ 320}.

Если   6 , то из первого уравнения

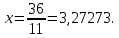
Подставим это в уравнение связи: y =1.85418 и y =-1,85418.

Таким образом, получаем еще две точки:

М₄(3,27273;1,85418), z₄=32,92591 ;M₅(3,27273;-1,85418), z₅=32,92591 .

Ответ: z_max=32,92591 , z_min 0

---

Смотрите также файлы

• Конкурс рисунков Безопасность глазами детей 22. 06.docx

• Компьютерная графика.doc

• Лекции Школа здоровья по профилактике заболеваний пожилого возраста и их профилактика (огбсу новоЛенинский дом интернат для престарелых и инвалидов) Лекции Школа здоровья.docx

• Математика в экономике.pptx

• План урока 81. Предмет Математика Урок 81 Школа Binom School им. А. Кекильбаева.docx