Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение

высшего образования

ИРКУТСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Институт заочно-вечернего обучения

Кафедра общеобразовательных дисциплин

Контрольная работа

по дисциплине

«Гидравлика»
Вариант № 50
Выполнил:

студент группы НДбз 18-2

Миронов А.В.

Проверил преподаватель:

Нижегородов А. И.


Иркутск 2020 г.

Задача 1

Автоклав объемом 25 л наполнен жидкостью и закрыт герметически. Коэффициент температурного расширения жидкости α, её модуль упругости Е. Определить повышение давления в автоклаве при увеличении температуры на величину Т. Объемной деформацией автоклава пренебречь.

Дано:

α = 956 · 10^-6 1/ºС

Е = 1,48 · 10⁹ Па

Т = 19,9 ºС.

Решение:

Температурное расширение жидкости при е. нагревании характеризуется коэффициентом температурного расширения α, который показывает относительное увеличение объема жидкости при изменении температуры Т на 1ºС:



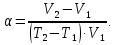
Учитывая, что 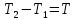, найдем V₂:





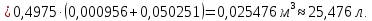
Коэффициент объемного сжатия β:



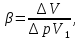
где ΔV – изменение объема V₁, соответствующее изменению давления на величинуΔp:

ΔV = V₂ – V₁ = 25,476 – 25 = 0,476 л.

Откуда определим повышение давления в автоклаве:



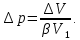
Величина, обратная коэффициенту β, называется модулем упругости:



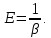
Тогда коэффициент объемного сжатия

---

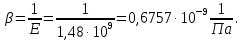
Повышение давления в автоклаве:



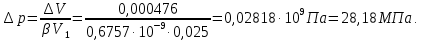
Ответ:

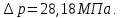
Задача 6

(рис. 10). Круглое отверстие между двумя резервуарами закрыто конической крышкой с размерами D и L. Закрытый резервуар заполнен водой, а открытый – жидкостью Ж. К закрытому резервуару сверху присоединен мановакуумметр MV, показывающий манометрическое давление р_м или вакуум р_в. Температура жидкостей 20°С, глубины h и Н. Определить силу, срезывающую болты А, и горизонтальную силу, действующую на крышку. Силой тяжести крышки пренебречь. Векторы сил показать на схеме.

Дано: Жидкость - бензин D = 640 мм = 0,64 м L = 530 мм = 0,53 м h = 2,15 м Н = 2,75 м рв = 28,9 кПа = 28900 Па Найти: Рв – ?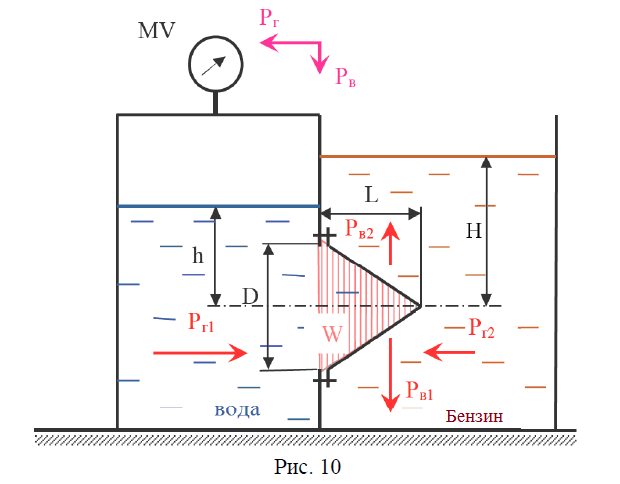

Решение:

Плотность жидкостей при температуре 20 °С:

- воды, ρ_в = 998 кг/м³;

- бензина ρ_бен = 745 кг/м³.

Площадь проекции конической крышки на вертикальную плоскость

ω = 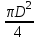= = 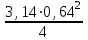0,322 м².

Объем конической крышки (тела давления)

W = 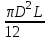= = 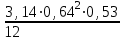0,0568 м³.

Результирующая горизонтальная сила давления на коническую крышку

P_г = P_г2 – P_г1,

где P_г1 – горизонтальная сила давления с левой стороны

P_г1 = (– p_в + ρ_вgh)ω;

где P_г2 – горизонтальная сила давления с правой стороны

P_г2 = ρ_бенgHω;

P_г = P_г2 – P_г1 = (ρ_бенgHω) – (–p_в + ρ_вgh)ω =

= (745 · 9,81 · 2,75 · 0,322) – (– 28900 + 998 · 9,81 · 2,15) · 0,322 =

= 6471,63 + 2527,92 ≈ 9000 Н.

Вертикальная составляющая равна весу воды в объеме тела давления (сила, направленная вниз)

---

P_в1 = ρ_вgW ;

Вертикальная сила давления, создаваемая бензином (сила, направленная вверх)

P_в2 = ρ_бенgW ;

Результирующая вертикальная сила давления (срезающая болты) на коническую крышку

P_в = P_в1 – P_в2 = ρ_вgW – ρ_бенgW = (ρ_в – ρ_бен)gW = (998 – 745) · 9,81 · 0,0568 ≈

≈ 141 Н.

Ответ: P_г = 9000 Н; P_в = 141 Н.




























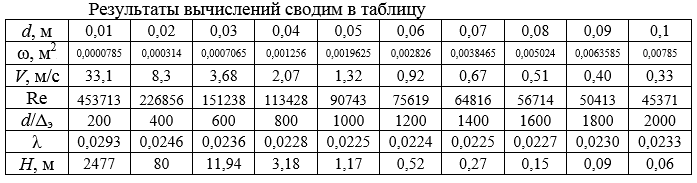
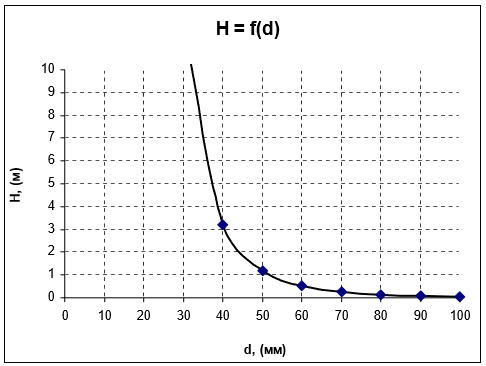
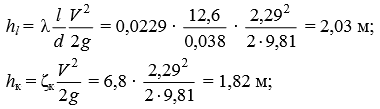
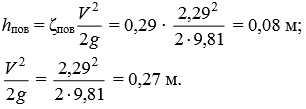
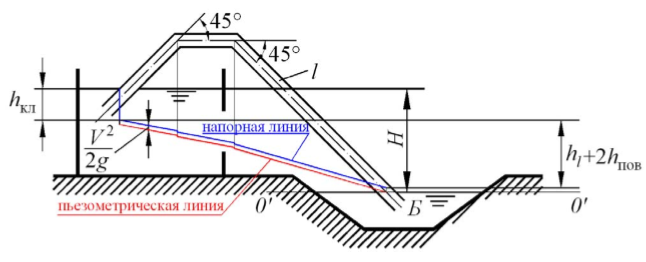
Ответ: d = 38 мм.

Задача 20

(рис. 24). Рабочая жидкость – масло Ж (веретенное), температура которого 50°С, из насоса подводится к гидроцилиндру Ц через дроссель ДР. Поршень цилиндра со штоком перемещается против нагрузки F со скоростью V_п. Вытесняемая поршнем жидкость со штоковой полости попадает в бак В через сливную линию, длина которой равна l_c, а диаметр равен

---

d_c.

Определить внешнюю силу F, преодолеваемую штоком при его движении. Давление на входе в дроссель определяется показанием манометра М, а противодавление в штоковой полости цилиндра – потерями давления в сливной линии. Коэффициент расхода дросселя принять равным µ = 0,64 , а диаметр отверстия дросселя d_д. Диаметр поршня D_п, а диаметр штока D_ш. КПД гидроцилиндра: объемный η₀ = 0,1, механический η_м.

Дано: Жидкость – масло Индустриальное 12 Vп = 4,50 см/с = 0,045м/с lс = 2,90 м dс = 11 мм = 0,011 м рм= 1,90 МПа = 1,9∙106 Па dд= 4,70 мм = 0,0047 м Dп = 90 мм = 0,09 м Dш = 25 мм = 0,025 м η0 = 1 ηм = 0,91 µ = 0,64 Найти: F – ?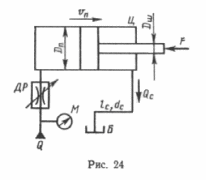

Решение:

Физические свойства масла индустриального 12 при 50°С (см. Приложение 1):

- плотность ρ = 883 кг/м³;

- кинематическая вязкость ν = 0,144 Ст = 0,144 ∙ 10^-4 м²/с.

Определим входной расход масла:



Условия расхода жидкости через дроссель:



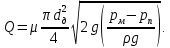
Откуда, найдем давление масла за дросселем (в поршне слева):





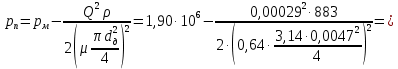
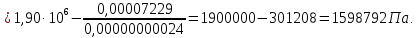
Определим расход масла через сливную линию:





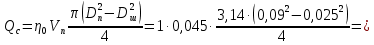
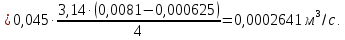
Скорость движения масла в сливной линии:



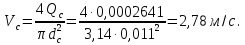
Определим число Рейнольдса в сливной линии:



Определим коэффициент гидравлического трения в сливном трубопроводе за формулой Блазиуса:



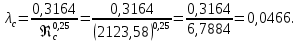
Давление в штоковой полости цилиндра:



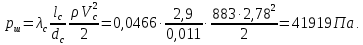
Составим уравнения равновесия сил приложение к поршню, учитывая механические потери:

---

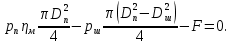
Откуда, найдем внешнюю силу F:







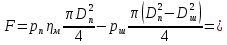
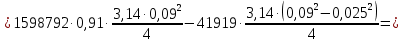
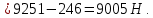
Ответ: F = 9005 Н.
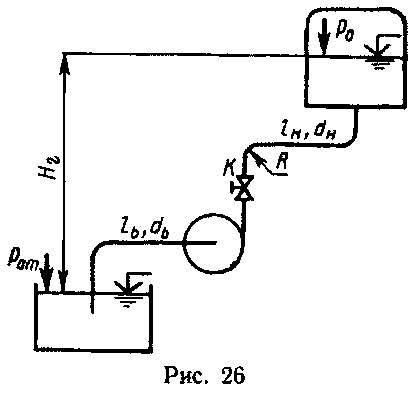Задача 22.5. (рис.26). Центробежный насос, характеристика которого задана (табл.2), подает воду на геометрическую высоту H_г. Температура подаваемой воды T = 20C. Трубы всасывания и нагнетания соответственно имеют диаметр d_в и d_н, а длину l_в и l_н. Эквивалентная шероховатость _э = 0,06 мм. Избыточное давление в нагнетательном резервуаре в процессе работы насоса остается постоянным и равно р₀.

При построении характеристики насосной установки из местных гидравлических сопротивлений учесть плавные повороты труб с радиусами R= 2d, сопротивление задвижки с коэффициентом местного сопротивления _з и вход в резервуар.

Найти рабочую точку при работе насоса на сеть. Определить, как изменяются напор и мощность насоса при уменьшении задвижкой подачи воды на 20%.

Таблица 2

Q, л/с	0,0	0,30	0,50	0,70	0,90	1,10	1,30	1,50	1,70	1,90
H, м	12,0	11,7	11,5	11,2	10,8	10,2	9,30	8,10	6,00	1,80
, %	0,0	34,0	50,0	60,0	65,0	69,0	70,0	68,0	62,0	51,0

Дано: вода; Т = 20°С;  = 998 кг/м³; ν = 0,010∙10^-4 м²/с

H_г = 3 м; l_в = 6 м; l_н = 17 м; d_в = 32 мм = 0,032 м; d_н = 16 мм = 0,016 м;

Р₀ = 30 кПа = 30∙10³ Па; _з = 0,50; _э = 0,06 мм = 0,00006 м; _вх = 1; _пов = 0,33

Определить: См. условие

Решение: Решаем задачу для Q = 1,9 л/с = 0,0019 м³/с

Скорости движения жидкости в трубопроводах:

---

Смотрите также файлы

• заслугу перед своим временем нам сейчас даже трудно вообразить. Самой значительной из них явилось то, что он впервые в истории.docx

• Лабораторная работа 1 2 Построение компьютерной модели 2 Лабораторная работа 2 7.docx

• .docx

• Омоложение мозга за две недели. Как вспомнить то, что вы забыли.pdf

• Методы и способы идентификации сбоев и ошибок.docx