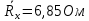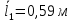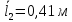Файл: Изучение сопротивлений при помощи моста Уитстона.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 03.02.2024

Просмотров: 10

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ

МИНИСТЕРСТВО НАУКИ и высшего ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего

образования

санкт-петербургский горный УНИВЕРСИТЕТ

Кафедра общей и технической физики
Отчёт по лабораторной работе №7

по дисциплине «Физика»

(наименование учебной дисциплины согласно учебному плану)

Тема: «Изучение сопротивлений при помощи моста Уитстона»

Автор: студент гр. ИГ-22-1 _______________ / _Татарчук В.А /

(подпись) (Ф.И.О.)

ОЦЕНКА: _________
Дата: _________

ПРОВЕРИЛ: _________________ / /

(подпись) (Ф.И.О.)
Санкт-Петербург
2023


Цель работы: 1. Изучение принципа работы измерительной мостовой схемы Уитстона.

2. Определение сопротивления проволочных проводников. 3. Определение удельного сопротивление материала.

Краткое теоретическое содержание

Явление, изучаемое в работе: возникновение электрического тока в электрической цепи

Постоянный электрический ток – упорядоченное движение заряженных частиц или, по – другому, электрический ток, который с течением времени не меняет свое направление и величину.

Электрическое сопротивление – физическая величина, характеризующая способность проводника препятствовать прохождению электрического тока.

Мост Уитстона – электрическая схема, предназначенная для измерения величины электрического сопротивления.

Реохорд – однородный проводник в виде металлической проволоки или струны с подвижным контактом, закрепленный на панели с измерительной линейкой.

Гальванометр – электроизмерительный прибор, имеющий высокую чувствительность к току или напряжению. В мосте Уитстона он используется в качестве нулевого прибора, показывающего отсутствие тока в ветви моста.

Законы и соотношения, описывающие изучаемые процессы:


Закон Ома для участка цепи:

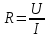, Ом

Формула для определения искомого сопротивления 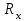имеет вид:

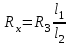, Ом

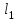где и 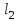- длины плеч реохорда

Таким образом, если вместо R3 включить сопротивление известного номинала и точно измерить по линейке расстояния 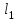и 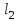, отвечающие условию IG = 0, можно определить неизвестное сопротивление Rx, включенное в схему моста.

Точное определение Rx позволяет найти значение удельного сопротивление проводника, в том числе неизвестного сплава, по формуле:

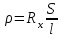, Ом * м

Правила Кирхгофа:

  1. Правило Кирхгофа

Алгебраическая сумма токов, сходящихся в узле, равна нулю, то есть количество зарядов, приходящих в данную точку цепи в единицу времени, равно количеству зарядов, уходящих из данной точки за то же время



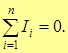
при этом токи, подходящие к узлу и отходящие от него, имеют противоположные знаки (подходящие – «+»; отходящие – «-»)

  1. Правило Кирхгофа

в любом замкнутом контуре цепи алгебраическая сумма произведений токов на сопротивления соответствующих участков контура равна алгебраической сумме ЭДС в контуре


Схема установки:

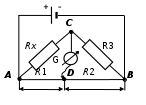
ɛ




Принципиальная схема моста Уитстона с реохордом

где Rx – неизвестное сопротивление

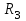- магазин сопротивлений МСР-63

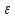- источник тока

R1, R2, 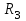– переменные сопротивления

G – гальванометр

D – движок

l1, l2 – длины плеч реохорда
Основные расчётные формулы:

Значение неизвестного сопротивления:

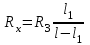, Ом

где 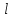‑ полная длина реохорда
Значение удельного сопротивления:

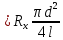, Ом * м

Погрешности прямых измерений:

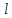∆ = ∆S = 0,0005 м

∆

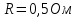
Формулы погрешностей косвенных измерений:

∆Rx = ( )

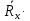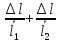∆ρ = ( )

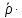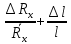Таблицы с результатами измерений и вычислений:

Таблица №1. Определение неизвестного сопротивления :

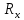№ опыта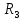
, Ом
l1, м
l2, м
Rx, Ом

1
10
0.91
0.09
101,1

2
20
0.83
0.17
97.6

3
30
0.77
0.23
100.4

4
40
0.71
0.29
97.9

5
50
0.665
0.335
99.3

6
60
0.62
0.38
97.9

7
70
0.585
0.415
98.7







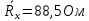
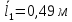
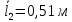
Таблица №2. Измерение сопротивления проволоки из константана:

Диаметр проволоки, d, мм
, Ом
l1, м
l2, м
Rx, Ом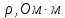


1
1.50
0.050
0.950
0.08



1
1.60
0.055
0.945
0.09



1
1.70
0.560
0.944
0.10



1
1.80
0.053
0.947
0.10



1
1.90
0.052
0.948
0.11



1
1.95
0.055
0.945
0.11

0.25



1
2.00
0.051
0.949
0.26



0,5
2.10
0.105
0.895
0.28



0,5
2.20
0.107
0.893
0.28



0,5
2.30
0.110
0.890
0.32



0,5
2.40
0.106
0.894
0.30



0,5
2.50
0.112
0.888
0.31



0,5
2.60
0.102
0.898
0.11



0,5
2.70
0.104
0.896
0.12



0,7
3.00
0.035
0.965
0.12



0,7
3.10
0.036
0.964
0.12



0,7
3.20
0.035
0.965






0,7
3.30
0.034
0.966






0,7
3.40
0.032
0.968
0.11



0,7
3.50
0.033
0.967
0.12



0,7
3.60
0.035
0.965
0.13













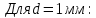
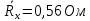
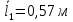
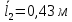
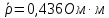
Таблица №3. Измерение сопротивления проволоки из неизвестного материала:

d = 0,35 мм



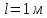
№ опыта
, Ом
l1, м
l2, м
Rx, Ом


1
6,8
0,5
0,5
6,8
0,654

2
6,6
0,52
0,48
7,15
0,688

3
5,9
0,54
0,46
6,93
0,666

4
5,4
0,56
0,44
6,87
0,661

5
4,9
0,58
0,42
6,77
0,651

6
4,5
0,6
0,4
6,75
0,649

7
4,2
0,62
0,38
6,85
0,659

8
3,8
0,64
0,36
6,76
0,65

9
3,5
0,66
0,34
6,79
0,653

10
3,2
0,68
0,32
6,8
0,654





Смотрите также файлы