ЛАБОРАТОРНАЯ РАБОТА

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

Вариант №5

П.М. БСТ-2154

ЦЕЛЬ РАБОТЫ:

• 
  Выбор физических моделей для анализа движения тел.
  
• 
  Исследование движения тела под действием квазиупругой силы.
  
• 
  Экспериментальное определение зависимости частоты колебаний от параметров системы.
  

b = 0,08 кг/с
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

Номер измерения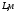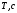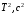
1	1,50	2,59	6,7081
2	1,40	2,49	6,2001
3	1,30	2,39	5,7121
4	1,20	2,29	5,2441
5	1,10	2,18	4,7524
6	1,00	2,08	4,3264
7	0,90	1,96	3,8416
8	0,80	1,84	3,3856
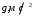	8,30 м/с2

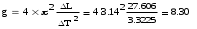
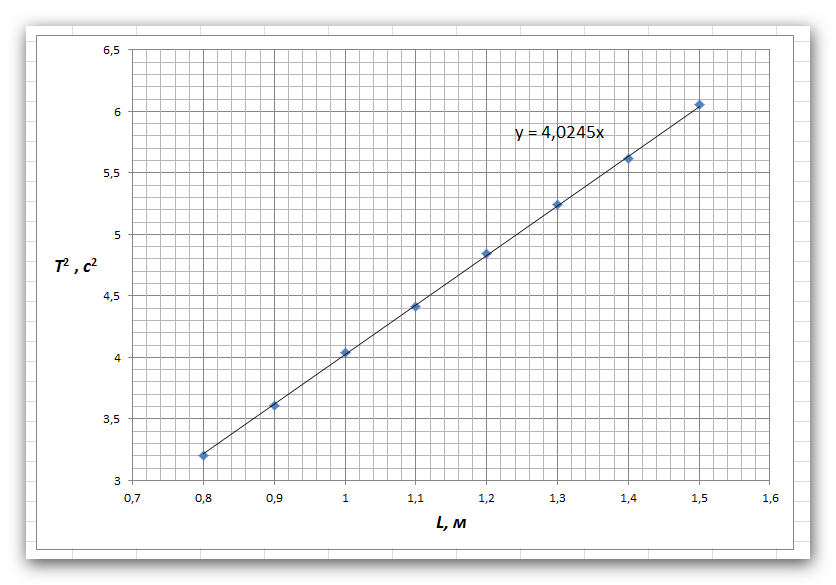
График зависимости квадрата периода колебаний от длины нити ММ

---

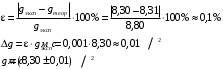
Вывод

С помощью модели математического маятника изучили механические колебания. Определили ускорение свободного падения 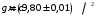. График квадрата периода колебаний от длины нити математического маятника имеет линейную зависимость.

Ответы на контрольные вопросы

1. 
   Что такое колебание?
   

Колебание – периодически повторяющееся движения тела.

2. 
   Дайте определение периода колебаний.
   

Период – минимальное время, через которое движение полностью повторяется.

3. 
   Дайте определение частоты колебаний.
   

Частотой колебаний называется количество полных колебаний за единицу времени. Частота - величина, обратная периоду колебаний.

4. 
   Дайте определение гармонических колебаний.
   

Гармоническое колебание – движение, при котором координата тела меняется со временем по закону синуса или косинуса: .

5. 
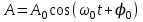   Запишите закон зависимости от времени характеристики А, совершающей гармоническое колебательное изменение.
   

6. 
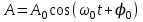
   Запишите закон движения МТ, совершающей гармонические колебания.
   

7. 
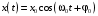
   Дайте определение амплитуды гармонических колебаний.
   

Амплитуда гармонического колебания А₀ есть максимальное отклонение параметра А от нулевого значения.

8. 
   Дайте определение фазы гармонических колебаний.
   

Фаза гармонического колебания 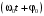есть значение аргумента гармонической функции.

9. 
   Дайте определение начальной фазы гармонических колебаний.
   

Начальная фаза гармонического колебания φ₀ есть значение аргумента гармонической функции при t = 0.

10. 
    Напишите уравнение связи частоты и периода гармонических колебаний.
    

11. 
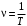
    Напишите уравнение связи частоты и циклической частоты гармонических колебаний.
    

12. 
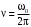
    Напишите формулу зависимости скорости ММ от времени при гармонических колебаниях.
    

---

13. 
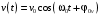
    Напишите уравнения связи амплитуды скорости и амплитуды смещения при гармонических колебаниях ММ.
    

14. 
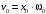
    Напишите формулу зависимости ускорения ММ от времени при гармонических колебаниях.
    

15. 
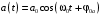
    Напишите уравнения связи амплитуды скорости и амплитуды ускорения при гармонических колебаниях ММ.
    

16. 
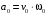
    Напишите уравнения связи амплитуды смещения и амплитуды ускорения при гармонических колебаниях ММ.
    

17. 
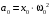
    Напишите дифференциальное уравнение свободных гармонических колебаний ММ.
    

18. 
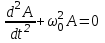
    Напишите дифференциальное уравнение свободных затухающих колебаний ММ.
    

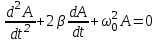, где  – коэффициент затухания.

19. 
    Что определяет коэффициент затухания?
    

Коэффициент затухания определяет, как быстро будут затухать свободные колебания в системе.

20. 
    Дайте определение математического маятника.
    

Математический маятник (ММ) это материальная точка, подвешенная на идеальной (невесомой и нерастяжимой) нити.

21. 
    Запишите формулу циклической частоты свободных колебаний математического маятника.
    

22. 
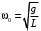
    Дайте определение пружинного маятника.
    

Пружинный маятник (ПМ) это материальная точка, прикрепленная к идеальной (невесомой и подчиняющейся закону Гука) пружине.

23. 
    Запишите формулу циклической частоты свободных колебаний пружинного маятника.
    

24. 
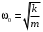
    Какие процессы происходят при вынужденных колебаниях?
    

При включении вынуждающей гармонической силы сначала происходит возрастание амплитуды колебаний с частотой, близкой к собственной. Затем возникает установившийся режим.

25. 
    Что такое резонанс?
    

Резонансом называется явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты

---

вынуждающей силы к определенному значению, которое называется резонансной частотой.

26. 
    При каком затухании резонанс будет более резким?
    

Резонанс будет более резким, если затухание в системе будет уменьшаться.

---

Смотрите также файлы

• Викторина География.doc

• Информация о проведении мероприятий Недели психологии.docx

• Устное и письменное деловое общение деловой этикет как состовная часть культуры общения.rtf

• Взаимодействие социальнопсихологической службы школы и учителя.pdf

• Строевая записка командира противотанковой батареи батальона укрепления границ.docx